Concept Circles for Exploring Exponents

We’re working on understanding what exponents mean, and how to represent them. To explore this topic today we used a concept circle framework at mild, medium and spicy levels of challenge.

Inside each concept circle, a manipulative is given, which will be used to create the models. We used toothpicks for x, skewers for y, and plasticine to connect them all together

Here are some photos of what students showed. The ideas to tackle with this circle is the idea of brackets, and how 2x² and (2x)² are different. What is in the brackets becomes the side length of the object. We also explore the difference between having an exponent of 2 and 3. We can explore visually how (2x)² = 4x², and how (2x)³=8x³.

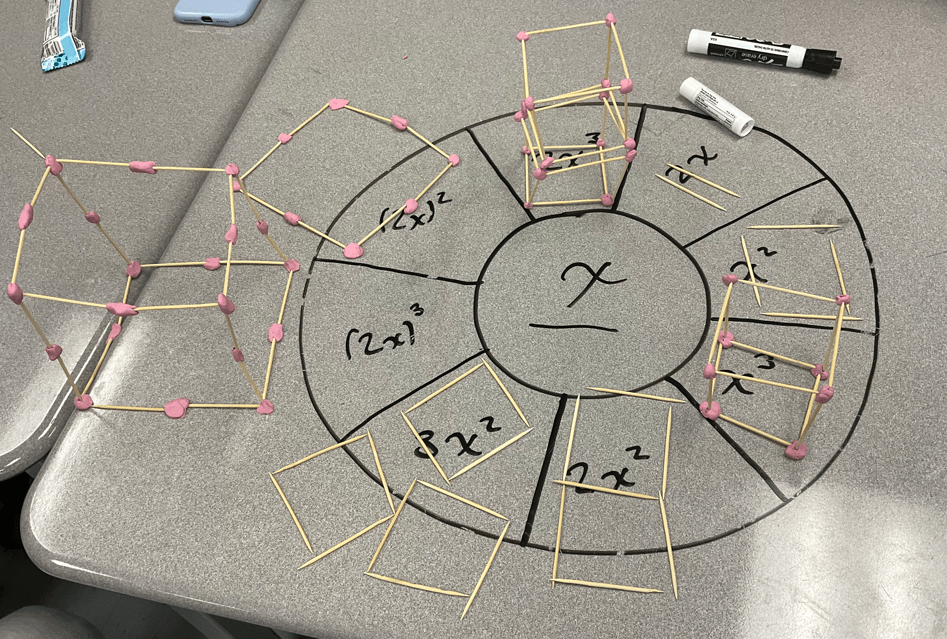
For the medium level, we introduce “half”, we talk about half an x, and half an x² and half an x³. We can talk about how the hypotenuse of the (1/2) x² needs to be longer than 1 toothpick. We reinforce the idea of what is in the brackets is the dimension of the object. We can explore visually how (1/2x)²=1/4x², and how (1/2x)³=1/8x³. We also review distributive property, and show how x(x²+x) can be represented as x³+x².

For the spicy level, students explored how to represent an x²y and an xy² as rectangular prisms, and also looked at (x+y)² and how it is not equal to x²+y².

At the end of the class, some students used their creativity to build a super mega cube, a (2y)³.

It has been pretty powerful for students to understand the difference between algebraic expressions using algebra tiles and now these toothpick figures. Students have a very solid idea about what like terms are, which will come in handy in future equation solving problems, as we move to more symbolic representations.