Math Buddies

We had an exciting morning today where we paired up a calculus and vectors class with a grade 10 class to work through a rich task that explores both sets of curriculum.

We have been using thinking classroom techniques and rich problems in both classes all term, so this approach was not novel, but this was the first time we had combined classes.  We have been working on building positive classroom communities, and this allowed students in both classes to shine.

We’ll walk you through the task here and give photos at the end (spoiler alert).

This task is from Al Overwijk who presented a deep dive OAME session last week, and were inspired to give this a try.

The task engages students to think about the number of ways to win at tic tac toe. First in a plane (the classic game) and then in 3 dimensions. 

The two classes were in one room, in visibly random groups mixing the grade 12s with grade 10s by choosing cards from a deck.  There were stations around the room for groups to go, each labeled with their card value.  Some groups ended up with only grade 10s, and some with only grade 12s, and many with a mixture.

To start we challenged a student to a game of tic tac toe.  Once a few games had been played, and everyone understood the game, the student groups decided how many winning lines there can be in a standard game of tic tac toe.

Next, the we introduced the idea of 3D tic tac toe, and how many winning lines can be made in a 3 by 3 cube of tic tac toe.  (think Rubix cube)

Students worked in groups to determine the number of winning lines.  Teachers were purposefully not so helpful, and just answered the “keep thinking” questions or clarified the task.

In the room we had a big bin of linking cubes, and if groups were looking to model in 3D they had access.  

As groups worked through their solution they needed to communicate on the whiteboards enough to convince themselves, their peers and the teachers that their answer was correct.

Helpful prompts were to consider if they had over-counted any winning lines, or missed any winning lines.  

Many students were stuck with the idea of tic tac toe being played on the surfaces of a cube, and not using the cube to play tic tac toe, so we had a quick reset partway through to discuss that the tic tack toe was happening within the cube.

We encouraged them to imagine a sphere taking up space in the cube so that they don’t end up over counting winning lines.

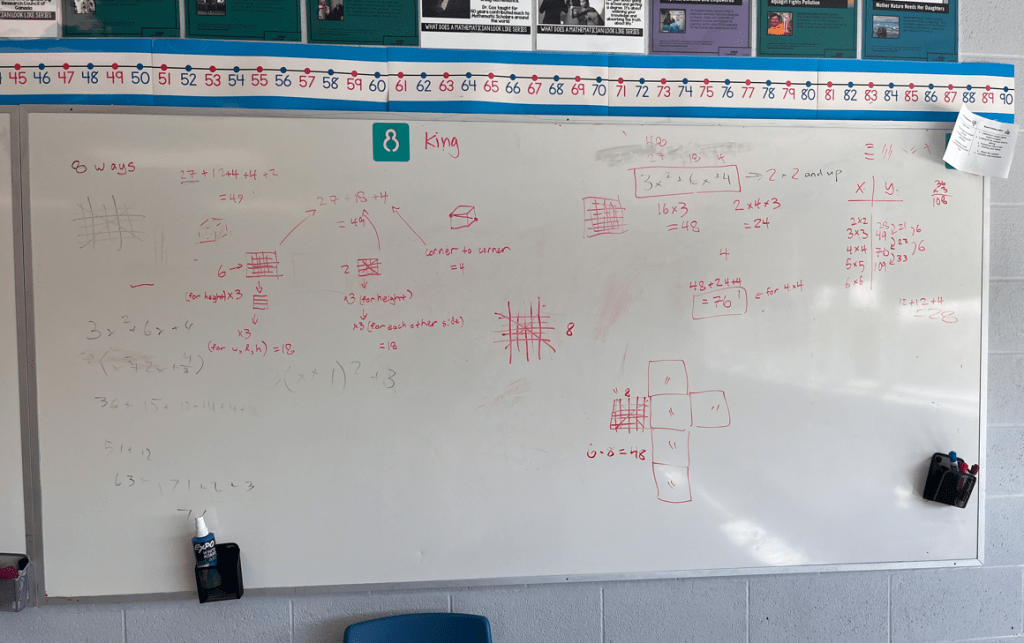
Once groups had succeeded in modelling the number of winning lines in a 3 by 3 cube, the extensions are to explore how many winning lines are in a 4 by 4 cube, and then 5 by 5 and then x by x.

Extensions can be varied, and some students stumbled upon them by their own inquiry

• Make a table
• Explore patterns
• Make a general equation
• Graph the relationship
• Explore the rate of change

Our consolidation involved:

• Going around the room looking at how everyone represented the question, to get everyone on the same page and value the diverse thinking and representation.
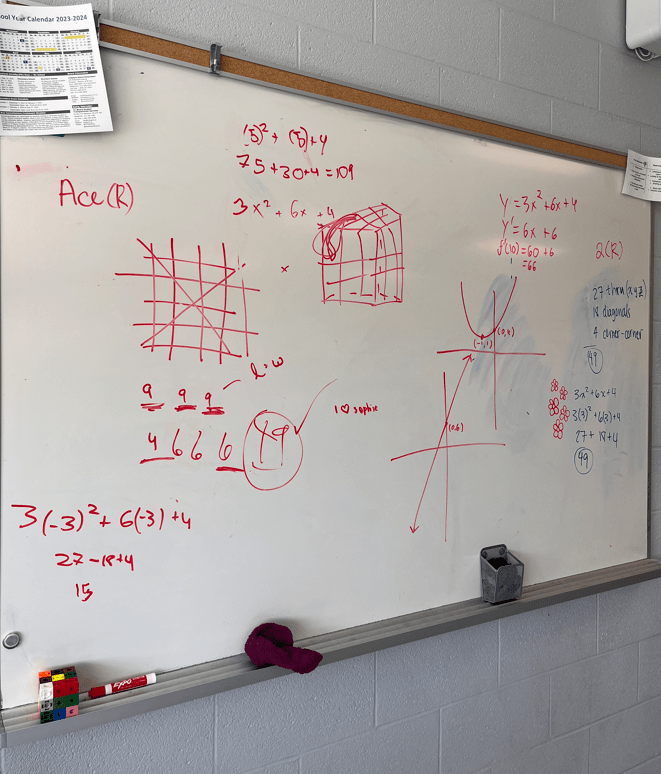
  • Pointing out various grade 12 ideas (vectors and planes, and x y and z axes) as well as grade 10 ideas of modeling quadratics, building the grade 10s up while congratulating the grade 12s for their collaboration and mentorship.
• Noticing and naming the strategies of using tables and equations and graphs.
• Consolidation did not focus on what the answer was, but rather on the methods and strategies used.
• The task led to a nice review of quadratic modeling and key features of quadratic functions.
• At the end, one group had a graph, and students were asking about if the problem could extend to negative x values.  The quadratic model does work well to show completing the square, visually, and we explored vertex form.

It was really fun to collaborate with a colleague, and to try something new. We will definitely try it again!