Angle Day

We got out the polygon tiles today in MTH1W and made some beautiful art. We can use our art to talk about a lot of math topics. In this image for instance, we can explore fractions, and see how we can use several different types of tiles to create hexagons. Each hexagon is made of 6 green triangles, or 3 blue rhombuses, or 2 red trapezoids.

We can use this image to explore some angle concepts. We can see that two of the triangle angles are equal to the obtuse angle on the blue rhombus and also equal the angle on the yellow hexagon.

we know that if we add up the angles in a triangle we get 180 degrees, and if it is equilateral, like the green, we know that the 180 degrees is split evenly among 3 angles. 180 divided by 3 is 60 degrees. We can conclude then that the obtuse angle on the blue or yellow is 120 degrees.

We can also explore opposite angles, as seen at the blue X. We know that angles that are opposite each other are congruent.

We can also add up the angles around a point (orange). We have 120 degrees (yellow), we have 2 green, each with 60 degrees, and 2 blue acute angles each with 60 degrees. If we add them all up we get 360 degrees. This is true around every point! The sum of the angles is 360.

I challenged my class to determine the angle measurements of each of these blocks. We can use the “sum of angles around a point” strategy to calculate the missing values.

At the centre of the design we have 12 beige rhombuses which make a full circle. We know that we can calculate the acute angle of the rhombus if we divide 360 by 12. That gives us an acute angle of 30 degrees. We can try to calculate the sum of the angles around the green dot to calculate the missing obtuse angle. We have a 120 degree yellow angle, and a 90 degree orange angle, and the remaining degrees needed to make 360 must come from the obtuse beige angle. 360-120-90=obtuse angle, 150=obtuse angle.

Another way to explore this is understanding that the sum of the angles in a quadrilateral is 360 degrees, so if you have two angles of 30 each, that leaves 300 degrees for both obtuse angles, and each obtuse angle must be 150 degrees.

We can explore supplementary angles too as a way to prove that the obtuse angle in the beige rhombus is 150 degrees. We know that the sum of supplementary angles is 180 degrees. These angles make a straight line when put together. Examine the yellow supplementary angles, we see 60+60+60=180. If we look at the blue supplementary angles we see that the acute angle is 30 degrees, so the obtuse must be 150 since they are supplementary angles and add to 180 degrees.

We got interested in figuring out what the interior angles of polygons were, and we built a table of values to check for patterns.

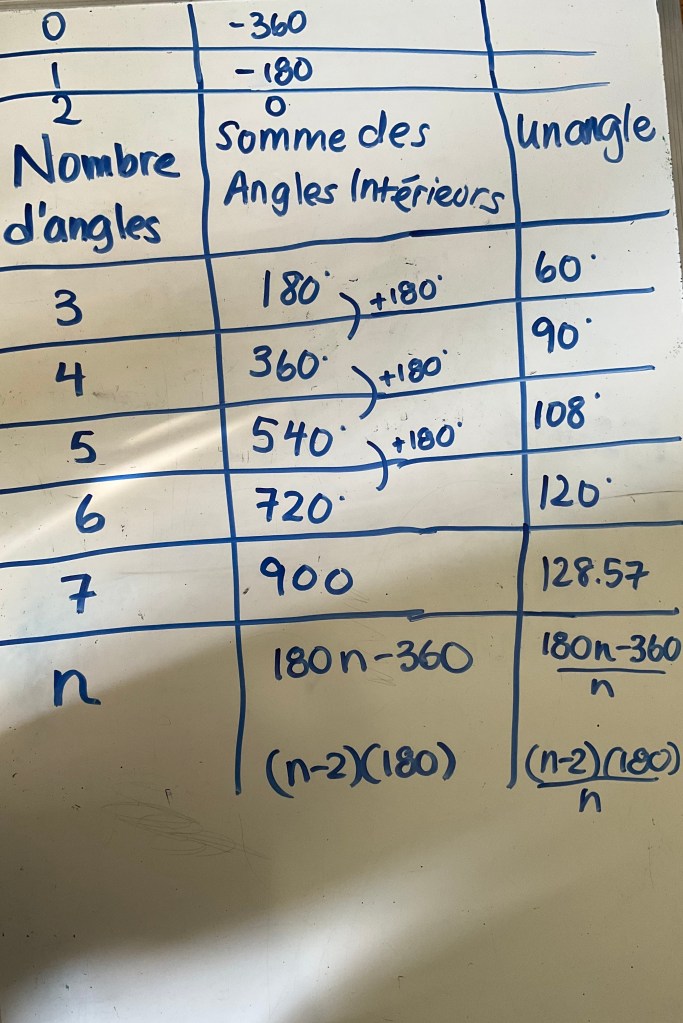
We noticed that the sum of the interior angles column increases by 180 degrees each time. We know that the rate of change (slope) is 180. We went back in the table to find the constant, which is -360. The equation for the sum of the interior angles in any polygon is SIA=180n-360

We noticed that the angle column doesn’t increase linearly since the first differences are not the same. We got the values by dividing the sum of the interior angles by the number of angles. We had an enthusiastic participant who explored what happens when we had a million sides on our polygon, and calculated that the interior angle would be 179.99 degrees. The class agreed that the polygon would look pretty circular.

To explore further, we graphed the angle values on desmos. We noticed that there is a limit to the value of the angle. It approaches but never reaches 180 degrees.

Our next steps are to explore the sum of the exterior angles, and also the value of exterior angles. More to come tomorrow!