Common Factoring

I’ve been working on a sequence for common factoring, as this has been an area of struggle for my students in the past. This time round, we started at the very beginning, finding the factors of 12, and the factors of 20. We wrote them all out:

12 is (1)(12) or (2)(6) or (3)(4) or (-1)(-12) or (-2)(-6) or (-3)(-4).

20 is (1)(20) or (2)(10) or (4)(5) or (-1)(-20) or (-2)(-10) or (-4)(-5).

We then looked for any common factors, which we identified. Then we looked for the greatest common factor. In this case it is 4.

Next I asked about the greatest common factor between 12 and 3x

Then the greatest common factor between 16x^3 and 12x

Then we looked at 45(x^2)(y^4) and 225(x^5)(y^3). Students noticed that the lowest power on each variable will be in the greatest common factor.

Next we looked at 38(a^2)(b^4)(c) and 14(a^5)(b)(c^2). Students were working on how to represent the factors and find the greatest common factor of 2(a^2)(b)(c). They also started to group the “leftovers” together.

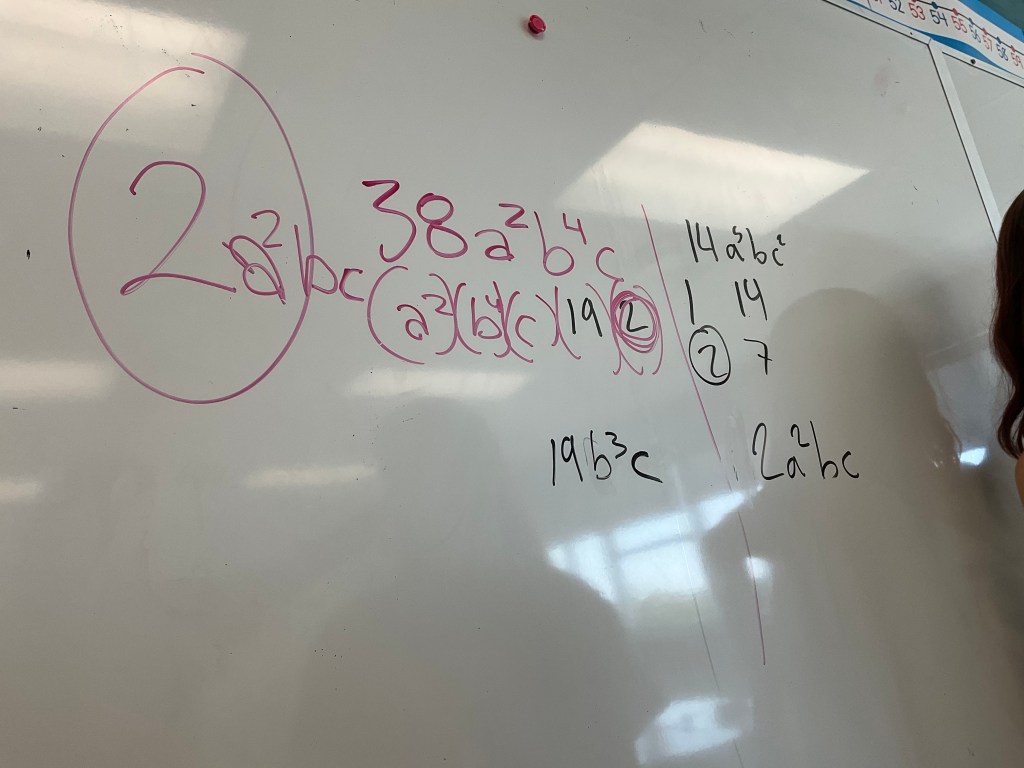
We next started to formalize a way to think through the process. We reviewed a bit about exponent laws in the process.

Finally we got to common factoring a polynomial. We find the greatest common factor, and put that outside of the brackets, and we end up creating a distributive property question with the “leftovers” (the not common factors) remaining in the brackets.

we can check our work with distributive property and exponent laws.

Students were keen to keep practicing. They asked for more and more chances to show that they got it. I’m pleased with how well the sequence went today, and am hopeful that retention will be strong. We’ll see next week!