Factoring and Expanding with Tiles

Today I had the pleasure of working with a grade 10 academic math class to help introduce factoring and expanding using algebra tiles.

To start with, students were working on recreating the rectangles provided and stating their areas and dimensions. Here is the sequence of questions we used.

We know the area is the insides, so that is x^2+8x+15, and the dimensions are (x+3) and (x+5). We know the long sides are x, and the short sides are 1, and we read the dimensions of length and width of the rectangle.

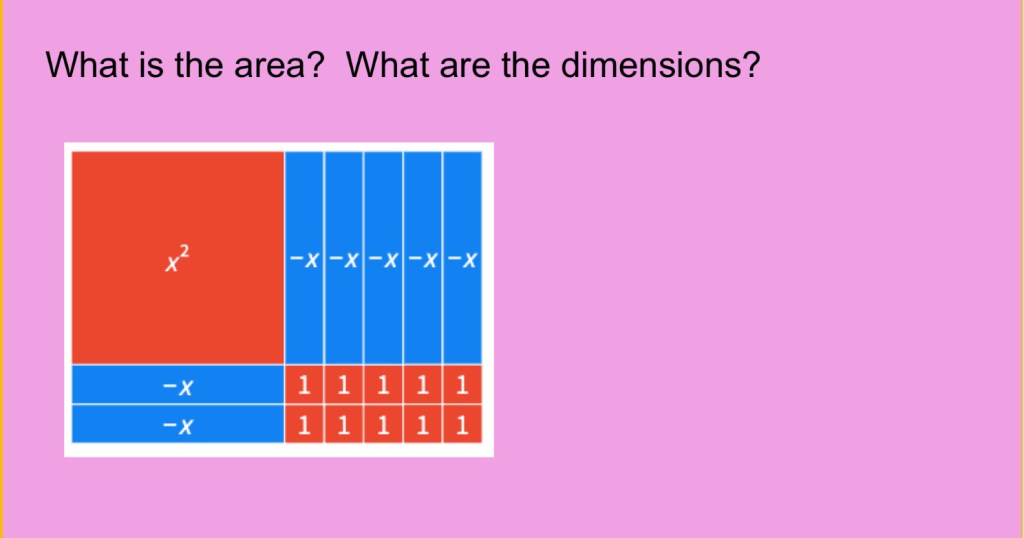
We looked at how negative times a negative is a positive, and that is why we need 10 red squares in the corner.

Here we looked at zero pairs, and how the +x and -x will cancel each other to make zero.

Students had to work on making rectangles from these given sets of tiles. The 2nd example allows us to talk about perfect squares. The 3rd and 4th require some zero pairs to make the rectangles work out.

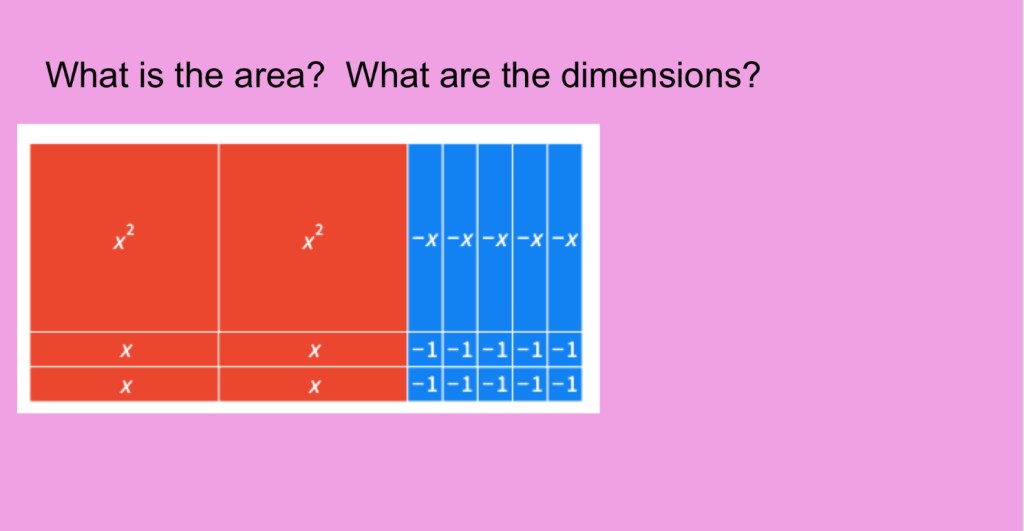
These examples have a few different ways to make rectangles. This is because there is a common factor of 2. We could split each polynomial up into 2 equal rectangles as well.

Finally, we tried giving dimensions, then building the rectangles to determine the area.

From these questions, students are essentially factoring and expanding using tiles. In spiral 2 we will go back and attach more algebra to these skills, and explore some patterns that are visible with the tiles.