Distance and Midpoint

We were up at the walls working on determining length of a segment, and midpoint of a segment today.

The sequence I used is as follows:

Plot the points (0,2) and (8,2). Determine the length of the line segment. (This is pretty simple to do by counting).

Plot the points (-1,-2) and (-1,4) and determine the length of the line segment. I asked students to think of how they could calculate the distance with operations. They decided that subtracting works 4-(-2)=6.

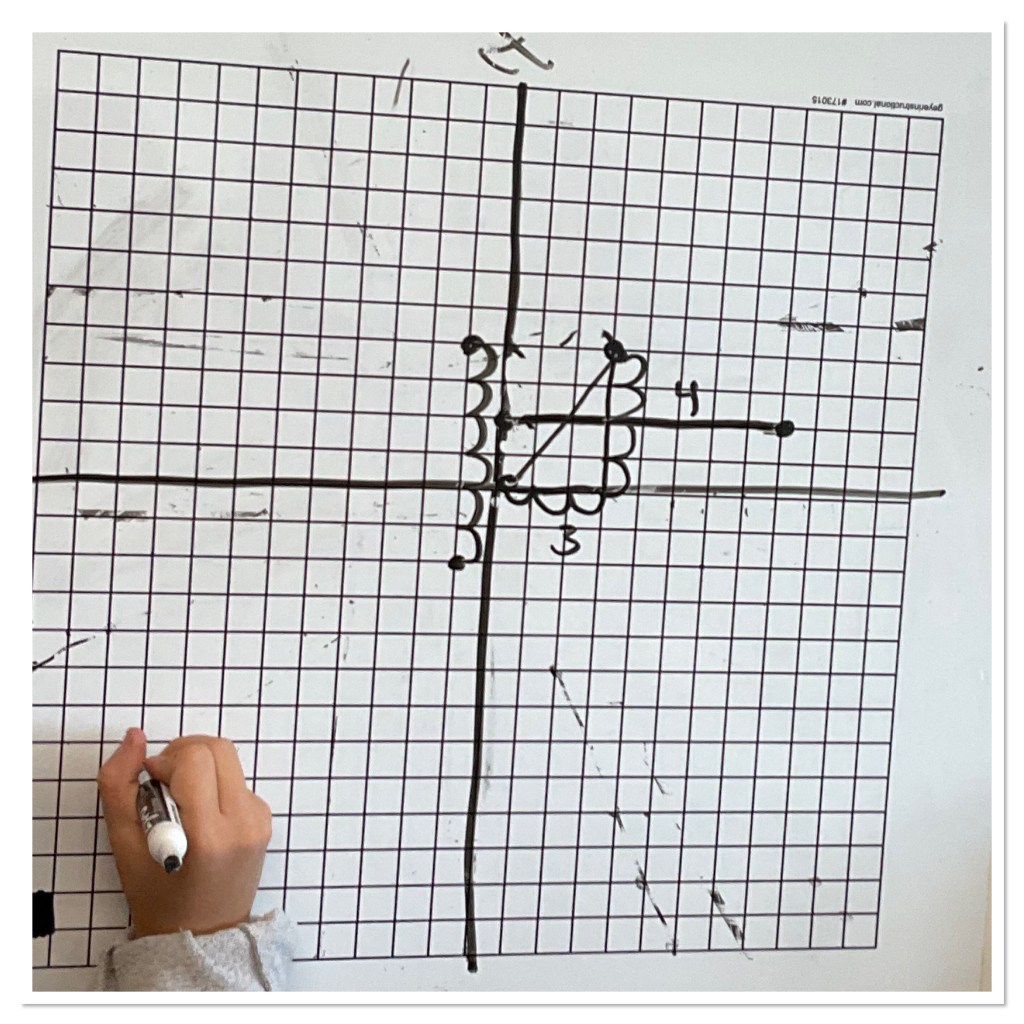
The next challenge was to find the length of the segment between (0,0) and (3,4). There was a bit of a struggle, until some students started to draw a right triangle to help.

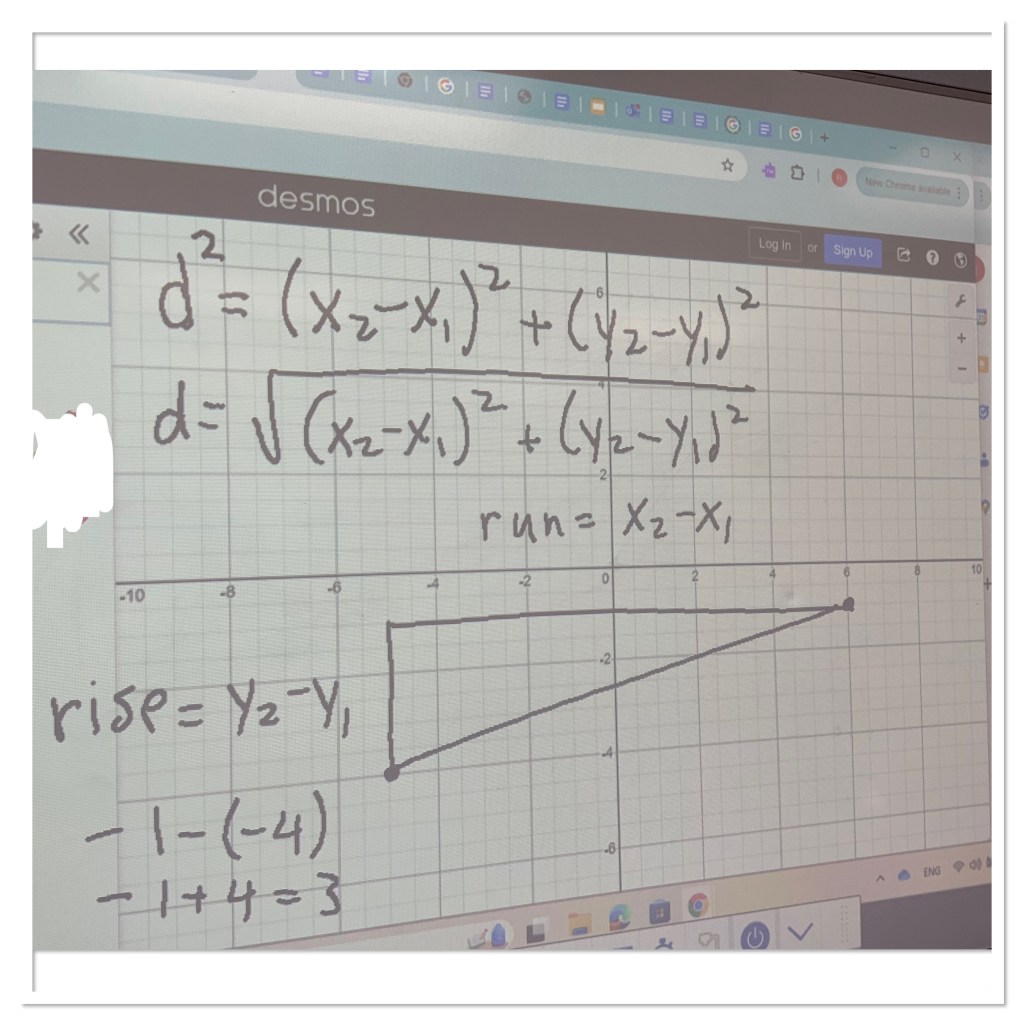
I asked some groups to try to find the distance between any two points (x1,y1) and (x2,y2). It was neat to see students use their idea of rise and run to create an equation.

We consolidated as a group and derived the distance formula that they will be given.

The sequence for determining the midpoint was similar. We looked at the midpoint of a horizontal segment, a vertical segment that had end points in different quadrants, and then for a segment that is on a slant.

It was interesting to see the connections that students made to their prior learning. Some were discussing the fact that a horizontal segment has a y value that is always the same, and a vertical segment has an x value that is always the same. Other students used the idea of finding the middle by taking the average. Pretty soon we were all taking the average of the x values, the average of the y values, and putting that in (x,y) form as the midpoint.