Representing Exponents

Today my grade 9 class built exponent models using toothpicks and plasticine. The mild version included x^2, x^3, 2x^2, 2x^3, (2x)^2, (2x)^3, 1/2x^2 and (1/2)^2.

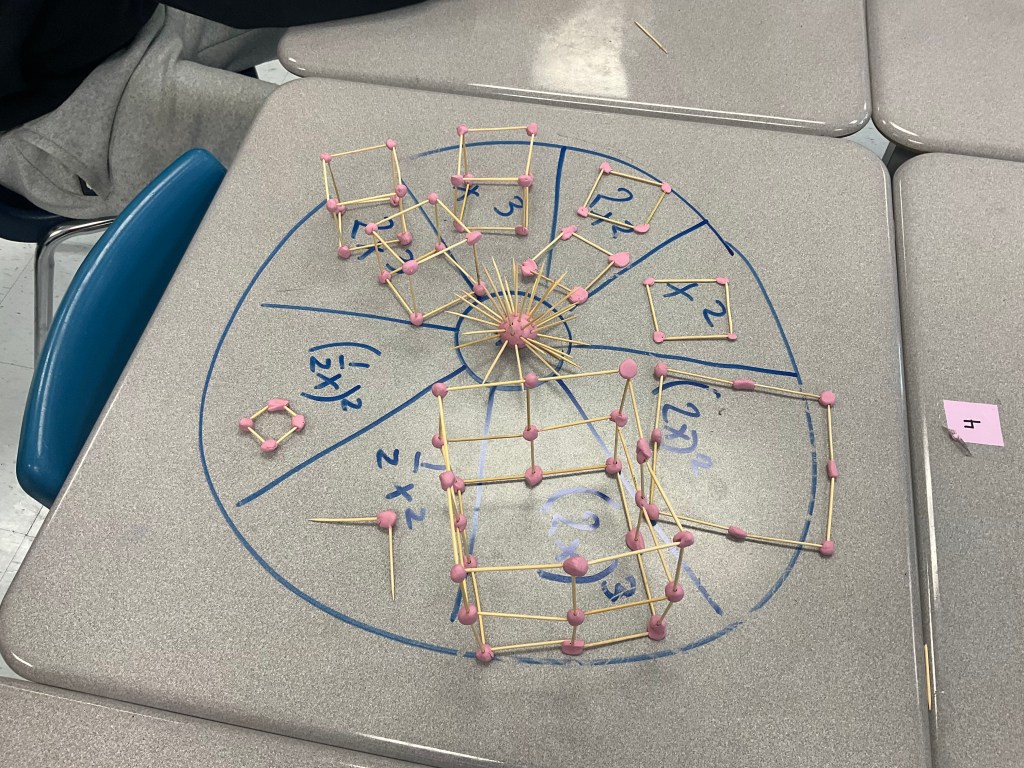
The x is a toothpick, so x^2 is a square (x by x). We made connections between the exponent being a 2 meaning we build a square, and if the exponent is 3 we build a cube. The base of the exponent represents the side length of the cube or square, and the coefficient will tell you how many to build.

We had a very carefully prepared (2x)^3. We can clearly see that it is made up of 8 little x cubes. This helps us see that if we double the side length of a cube, the volume will be multiplied by 8 (2^3=8). In the same photo you can see a (2x)^2 which helps us see that there are 4 x squares in it. When the side length of a square is doubled, the area is multiplied by a factor of 4 (2^2=4).

We moved on to a spicy concept circle, including skewers for y and toothpicks for x.

We had some interesting conversations about where to start. Some groups gravitated to the (x+y)^2 since they knew they were making a square with side lengths of (x+y).

We were able to split up the (x+y)^2 into x^2+y^2+2xy. We also showed that (x+y)^2 is NOT equal to x^2+y^2.

Other groups got into building the rectangular prisms with dimensions (x)(y)(y) or (x)(x)(y)

We noticed that an x^2y and an xy^2 were not the same. We could identify which was which based on the square that we saw. This one in the picture is an xy^2 since we see the skewers making a square.

I think we had many lightbulb moments today as we explored what exponents mean. We will continue exploring exponents for the next few days as we look at exponent laws.