Exponent Laws Continued

Grade 9s were hard at work today continuing on their exponent laws journey.

We explored some examples with numbers.

We learned that if we have a fraction with the same numerator and denominator it simplifies to 1. Each of the circled pairs will simplify to 1. We can now express the answer as an exponent. When we divide and the bases are the same, we can subtract the exponents.

This works if the base is a variable as well.

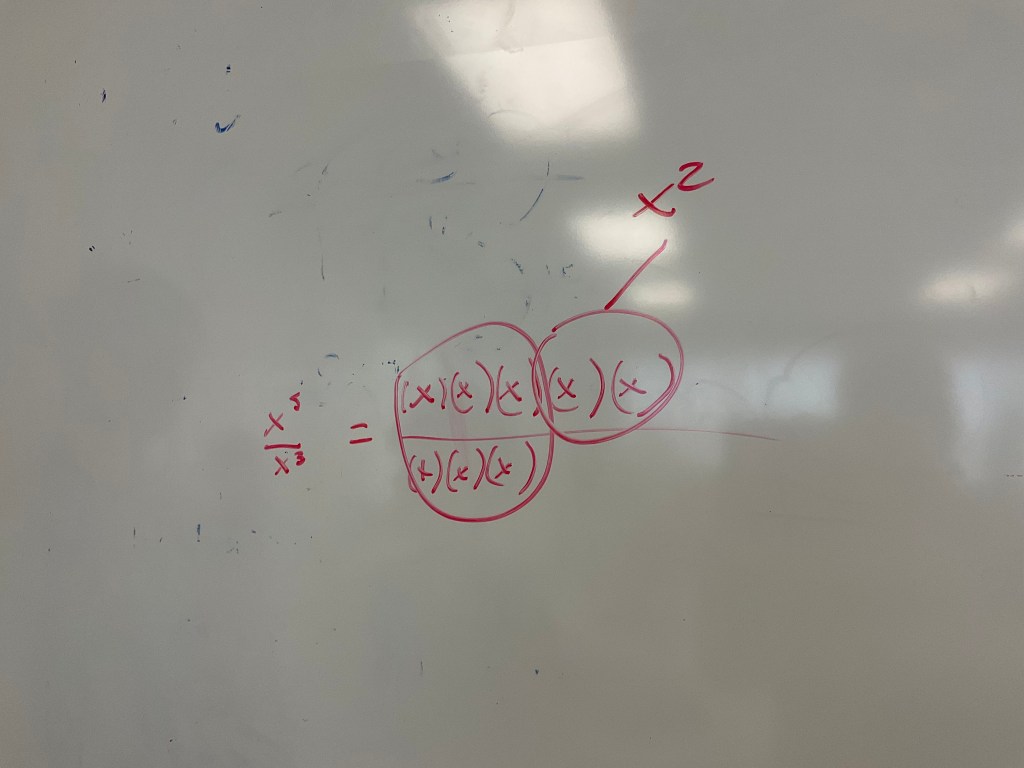
The next example includes coefficients and 2 variables. We know that we divide the coefficients as normal. 12/6=2. We look at the xs next. We have x^(4-2) which is x^2, and something neat happens with the ys. We see that when we subtract the exponents we get 0. We also see that we can circle the y^3 in the numerator and denominator and that this fraction will equal 1. Anything to the power of 0 will be equal to 1.

The next example leads us to explore negative exponents. We can easily manage the fraction and the as, but when we have b^(4-6) that leaves us with b^(-2).

We explored how to write negative exponents another way. When we have a negative exponent, it has come from a case where the exponent in the denominator is higher than the exponent in the numerator. If we write it in developed form and circle all the fractions that equal 1, then we will be left with variables in the denominator. a^(-2)=1/(a^2)

We consolidated our work, and made a note in quadrants. Students made their own examples, and we co-created a list of things to remember and write down.

I sent a mass email to students and families with this homework task: Students should explain how to do this question tonight or over the weekend.