Fractions, Decimals, Percents

Grade 9s are going to be working with fractions and decimals and percents coming up. Today we worked on putting them in order, as a diagnostic collaborative activity. I’m uncertain which gaps exist in this class due to what work would have been missed during COVID lockdowns years ago. There have been different gaps this year that I have noticed, with perimeter, and I wondered if fractions may have also fallen through the cracks more than in the past.

Students worked in their randomly selected table groups. Groups were given a handful of assorted cards. White cards are fractions, green are percents and yellow are decimals. They needed to work together and use their strategies to sort the cards from smallest to biggest.

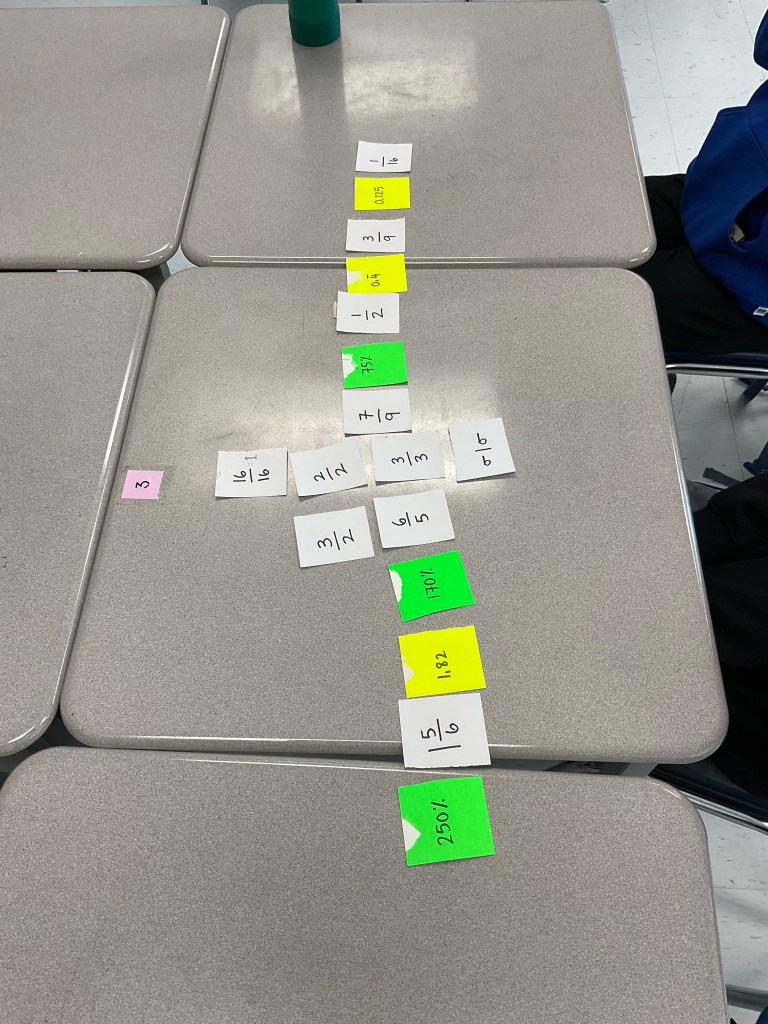
Groups chatted about how to tell if fractions were big or small (if they were in mixed numbers they looked for the whole numbers, they also looked for improper fractions where the numerator is bigger than the denominator). They were very confident ordering decimals, and ordering percents, but putting decimals and percents together took some thinking.

Each group then sent a volunteer with their smallest value to chat and decide what the smallest smallest value is, and we started a communal number line. They sent a different volunteer with their largest values to chat about which one was the largest largest value and put the other end point of our number line on the board. Next everyone placed their cards in order, and made sure the number line made sense.

We talked a bit about what fractions mean, and how to represent them, and we chatted a little about what numerators and denominators are. We learned that if we divide numerator by denominator we can make a decimal, so we can convert fractions to decimals and compare the numbers nearby. We also noticed that decimals and percents differ by a factor of 100, so to convert decimals to percent we multiply by 100% and to change percent to a decimal we divide by 100%.

We talked about comparing fractions as well. If the fractions have the same denominators we know that the unit rectangle is split into an equal number of pieces (the denominator) but we are discussing different quantities of pieces. E.g, 3/5 compared with 2/5 we know that the unit rectangle is split into 5 pieces. One fraction talks about 3 of the 5 pieces, and the other fraction talks about 2 of the 5 pieces. I know 3/5 is bigger than 2/5.

If the numerators are the same and the denominators are different we can compare them easily as well. E.g. 3/8 compared to 3/9. I can imagine a rectangle split into 8 pieces and a rectangle of the same size split into 9 pieces. If it’s split into more pieces the pieces are smaller. If I have 3 larger pieces compared to 3 smaller pieces, I can conclude that 3/8 is larger than 3/9.

We then worked on correcting the order in the number line.

The final challenge was to space our numberline properly. We set benchmark values of “friendly numbers” like 0, 0.5, 1, 1.5, 2, 2.5 and then each table group sorted and spaced one of those sections of the number line.

We have some work to do, but during this activity students were able to explore and try and reactivate ideas from years ago. Some expressed that they were very unsure of fractions in general. We will work on these topics for a while, then try a similar task later and see if they feel better about the strategies we have learned.

I captured photos of their finished numberline. We may look back at these photos next week and see if we can find things to correct, or discuss.