Patterns, Equations and Graphs

Today I was invited to work with a class on patterning, and equations and graphing.

We built and extended the pattern using square tiles. We noticed that we added 2 new tiles each time, and we can see that we always add the new tiles in the same place. We can also see that figure 0 would have 1 tree. Figure 0 is the constant. It’s always there. We thought about how many trees would be in figure 10, or figure 100. We could make a table, and we could add 2 and add 2 and add 2 until we get to figure 100, but that is tedious, so we can think about how many groups of 2 you added. To get to figure 100 we add 2 100 times to the 1 that we started with. To get to figure x, we add 2 x times to the 1 that we started with. The equation, or pattern rule, is y=2x+1

We had some fun building our own patterns and sharing the rules.

We saw some neat patterns:

this one is y=2x+1

the figure 2 is a bit different here, but the pattern was cool, going up by 6 each time, we’d need a negative constant.

i was impressed at how many groups made negative constants without any issue. I likes how we have different colours for positives and negatives in these representations.

this was a neat pattern that was fun to unpack. We looked at how it grew and noticed that it was not linear because we added different amounts each time. We saw that we could split the figure into a square and 1 extra tile. The constant is 1 since figure 0 is 1. We determined the equation was y=x^2+1.

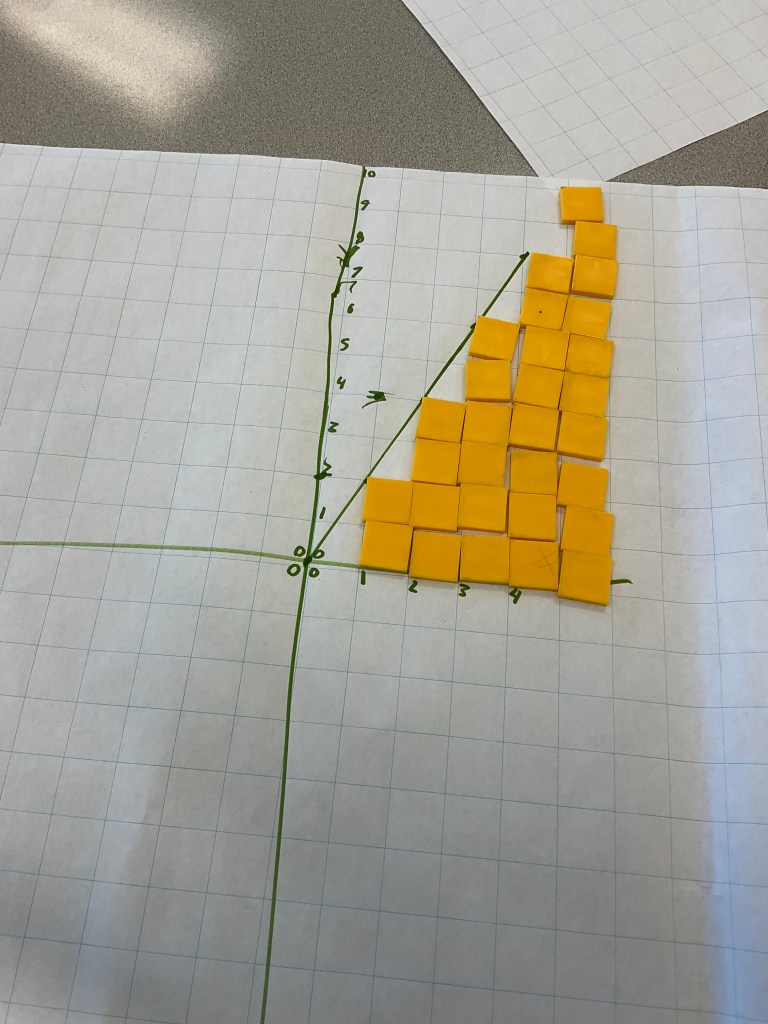
Groups had 2 pattern rules to explore and graph on the same axes with different colours.

here are the results:

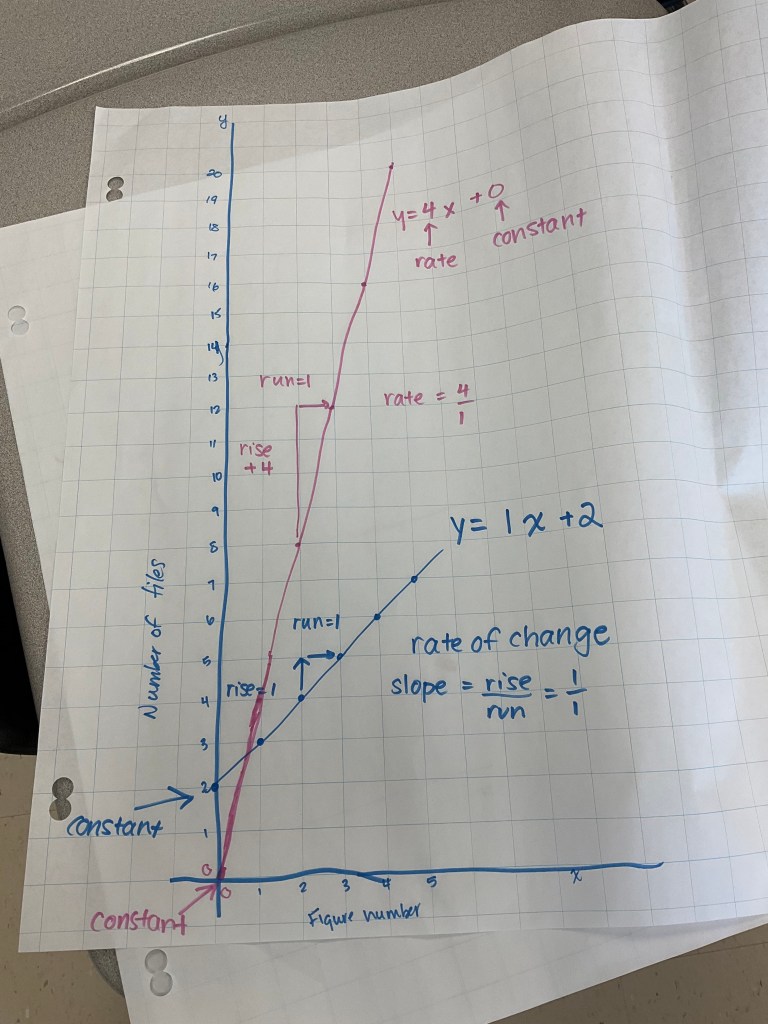
these two lines are parallel, they have the same slope, and different constants, and they will never intersect.

Many thanks to the class for inviting me to come share some activities. I hope to be back again to try something similar with quadratic patterns!