Painted Cube Revisited

I was invited to run through the painted cube problem for another class of grade 10s. With each iteration of these rich tasks it’s neat ro see the different connections that can be made.

To refresh: the task is to imagine that a 3×3 cube is dunked in paint, then dried, then disassembled. We need to categorize each little sub cube by the number of faces that have paint.

Once groups have managed a 3x3x3 cube, they are asked to try a 4x4x4 or a 5x5x5 or a 6x6x6 or a 10x10x10 or the general case of (x)(x)(x).

Students come up with all the equations to model the relationships, then are asked to graph the relationships.

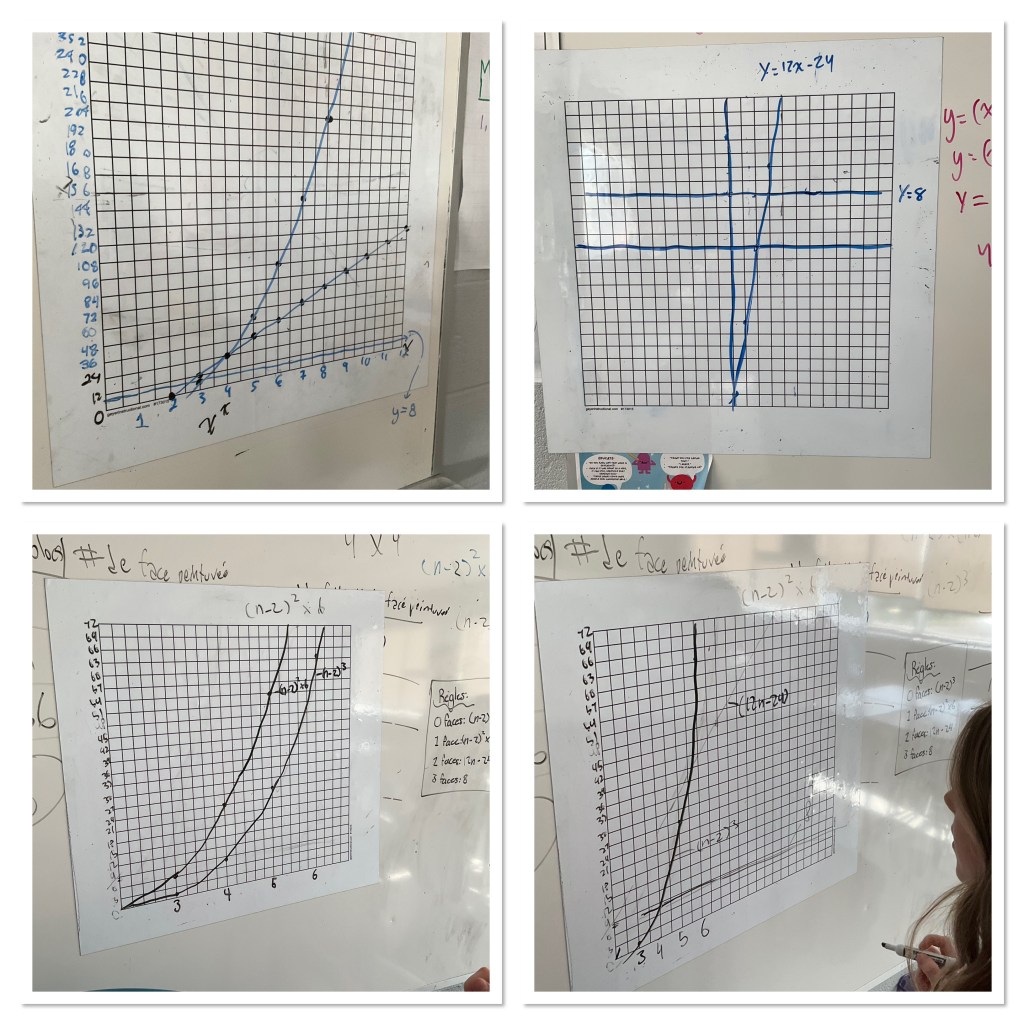
What was interesting with this group was that they wanted to find the intersection of the curves algebraically. We got into some good discussions about how to multiply a binomial by a trinomial, and also about how to solve by substitution.

we discovered later that the best way to approach this particular intersection in grade 10 is with u substitution, since we can’t really deal with factor theorem or solving cubics.

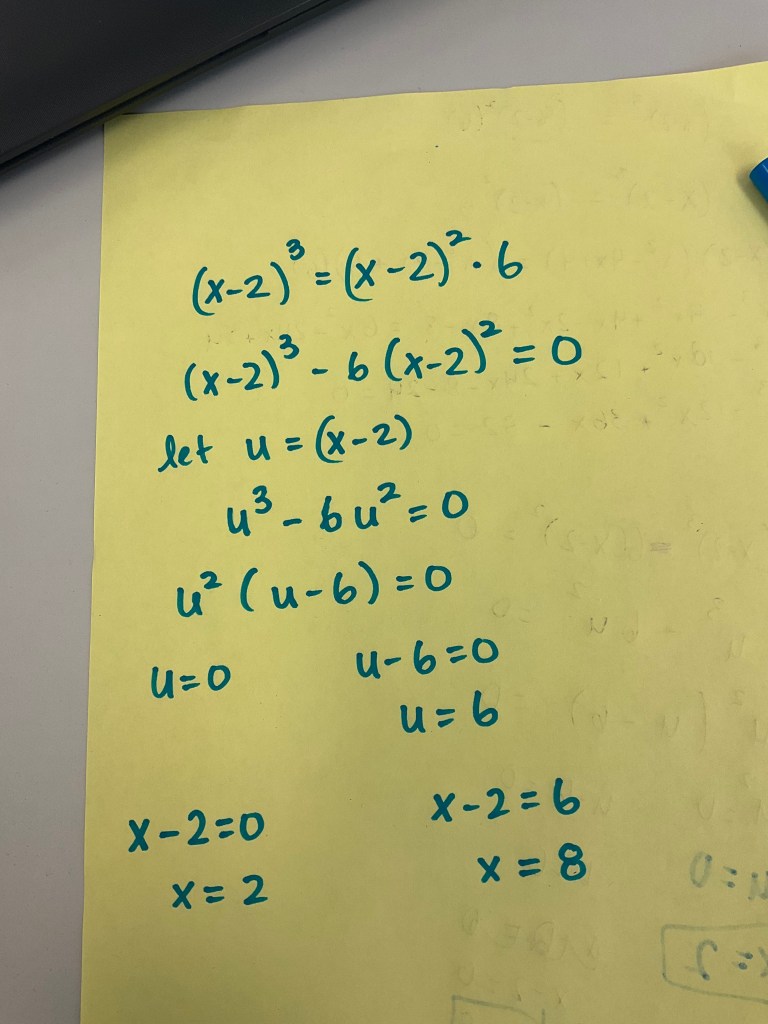
The other intersections are all really good to do for grade 10s. It’s good practice for solving linear systems by substitution, or solving systems by factoring.

This task gets richer with each iteration! Looking forward to seeing what we notice the next time through.