Completing the Square

For the last 2 days I’ve been working with a grade 10 class on completing the square. We’ve used algebra tiles and visual representations to make sense of the algebra that is required, and we’ve made connections between vertex form and graphs of parabolas.

Day 1 we worked on writing expressions in standard form and vertex form

We worked on building squares, and writing them as perfect squares, and including any extra tiles as “extras” outside the perfect square. We know that we can put red unit tiles in the bottom right corner because they “complete” the square, but we can’t ever put blue ones there because (+)(+)=(+) and (-)(-)=(+), ans squares have identical sides.

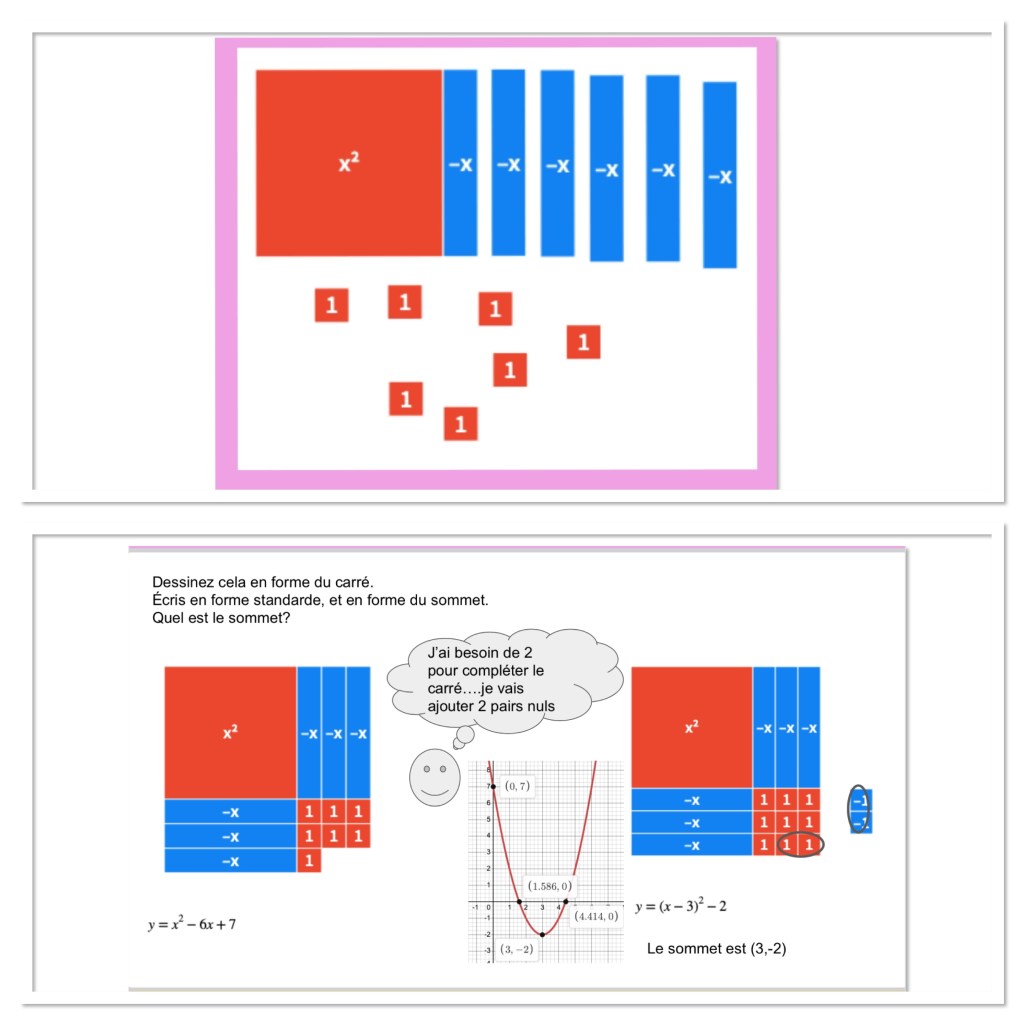
Sometimes when we don’t have enough to complete the square, we need to add more unit tiles. We have to do this carefully though, and add zero pairs. The positive of each pair can fill the square, and the negative of each pair will be outside.

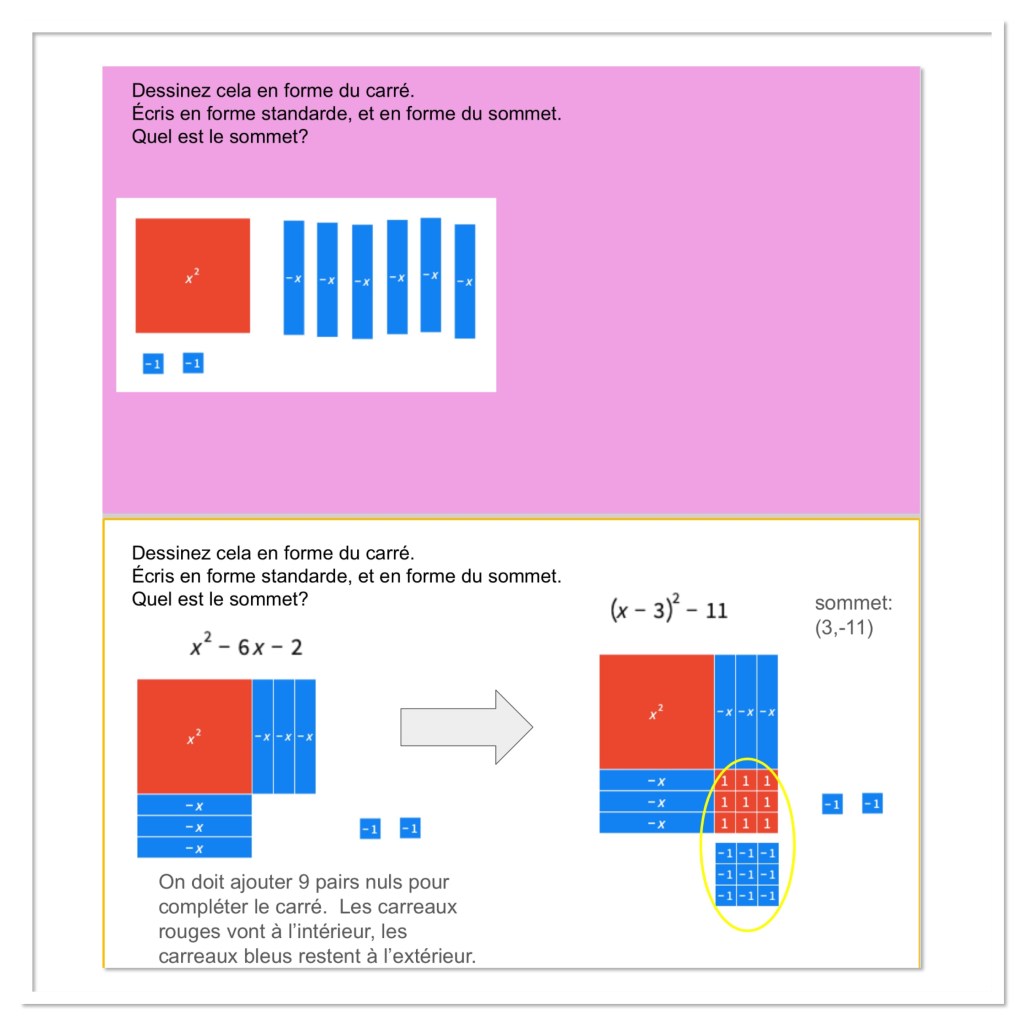
If there are only negative unit tiles they can’t go in the square, so we fill the square completely with positive tiles, and have the negative part of the zero pair join with the negative unit tiles.

Here we complete the squareS. This was my big algebra tile breakthrough, when I understood how to complete the square with a leading coefficient. We need to create identical squares. We do the same steps. It’s beautiful!

Students got really good at completing the square(s) and stating the vertex and direction of opening, and using their logic to see if there would be x intercepts or not.

Day 2

we did some review of day 1 material with students in random groups at the whiteboards around the room, and then I slid in a challenge to cause some productive struggle. These numbers don’t work out nicely.

students had excellent conversations about how to use all the x tiles and create squares. Once they realized that x tiles could be “cut” we had some progress! This was not an easy question, but wrestling with it helped us sew if the students were understanding what they were doing, or if they were following a rote procedure.

Next we looked at completing the square if the leading coefficient is negative. To do so, we common factored a -1 from each term, held that aside, completed the square of what remained, then multiplied the -1 back into the question.

For fun, we kept going, and explores how to calculate the x intercepts when we have the equation in vertex form. We set y=0 and used opposite operations to isolate x.

we even saw what happens when we have no x intercepts when we use this method. We’d end up trying to take the square root of a negative, which we know doesn’t work, so there are no x intercepts. It is fun to learn how to interpret situations where the math says “no”.

it was a busy 2 days with lots of good learning and participation. Many thanks for letting me join and work with the class!