Multiple Strategies

Quadratic word problems are my favourite kind of problem because there are so many strategies to solve them. Here’s an example of one we solved today.

It’s a question about when a farmer should harvest her potato crops to maximize revenue. There are initially 100 bushels that can be sold for $2/bushel. For each week she waits the price per bushel drops by $0.10, and the number of bushels grows by 100.

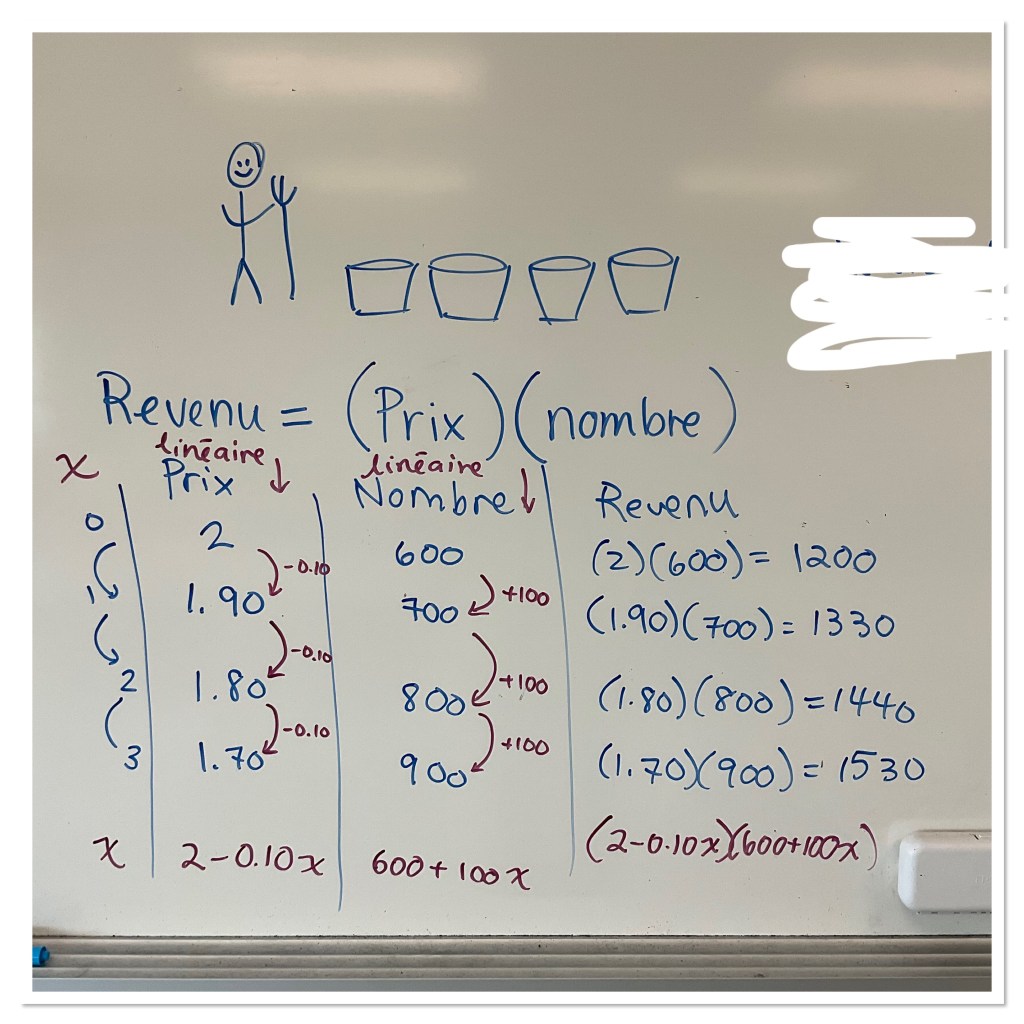
My students were unsure of how to start the analysis, so we looked at a strategy of making a table to help us organize our thoughts and generalize patterns. Some students really like making a table as a solution method. It’s time consuming, but would work eventually. We talked about how to make the solution more efficient by making an equation for revenue using x as the number of weeks that the farmer waits.

Once we modelled the situation with an equation we split into groups to try to solve for the number of weeks x to wait to have a maximum revenue.

some groups decided to multiply the binomials to start, and then did the quadratic formula to solve for the x intercepts. Most got bogged down after doing all this math and forgot that they were looking for the vertex (which falls always between the 2 x intercepts). Sometimes our solutions are looking for x intercepts, some for the vertex, we’re looking at interpreting word problems correctly and looking for words like maximum, maximize, minimum, minimize to hint at when we need to find the vertex.

Once we noticed (by looking around the room) that some groups concluded that the farmer should wait 20 weeks and others got a different, smaller, answer I prompted them to substitute in their weeks number for x and to calculate the revenue. When groups noticed that when they subbed in 20 the revenue was zero, they realized they needed to rethink some things.

Some groups noticed we had started with a quadratic in factored form, and that we could solve for the x intercepts by looking at the cases that give revenue=0

Prompting the groups to do a little sketch was helpful for them to start to find the vertex.

Groups around the room started to realize that they could get to the x intercepts in 2 ways, by solving for what makes the brackets=0 from factored form, or from the quadratic formula. Both methods require a quick calculation to find the axis of symmetry.

While these methods were percolating and spreading around the room, another group headed down the road of completing the square to locate the vertex (before getting side tracked).

While consolidating we looked at how this strategy also would work nicely. As long as we correctly managed the negative sign at the start.

In this example we can factor out -10 and the numbers are still nice to work with, so we factored -10 then completed the remaining single square, and then multiplied the -10 back in the end. This method directly finds the vertex, which allows us to find the number of weeks the farmer should wait AND the maximum revenue she’d earn.

We had a nice chance to debrief and talk about choosing efficient strategies to solve. Based on what we are given and what we are asked for it might make more sense to use one method over another, so it’s great to have many strategies in your back pocket.