How Many High Fives?

Today in grade 10 we explored how many unique high fives there were in the room. We defined a high five as unique when person A high fives with person B. If Person B then high fives person A it doesn’t count.

Some groups got right to making tables. We had 15 people in the room today.

Once the situation was explored and understood, we clarified thar one could not high five themself…that’s called clapping… we kept working on the problem.

some groups drew it in pictures. Each line represents a high five.

Other groups wrote out all the high fives that would happen in a list, then totalled them up.

They noticed some patterns, and were able to make an equation for the pattern.

Another group modelled what would happen with a small group. We know that with 1 person there are no high fives, and with 2 people there is 1, and with 3 people there are 3, and with 4 there are 6. We kept adding more people to the group and they did the high fives and counted. Eventually a pattern was noticed, and identified as quadratic since the 2nd differences are all 1.

Some new learning today is that the “a” value is going to be half of the common 2nd difference.

The table could be extended backward to find the constant, c, 0 persons have 0 high fives, so the constant is 0. Next a point was subbed in for x and y and b was calculated.

There were some neat graphs that were made. This group showed the number of high fives per person, and total.

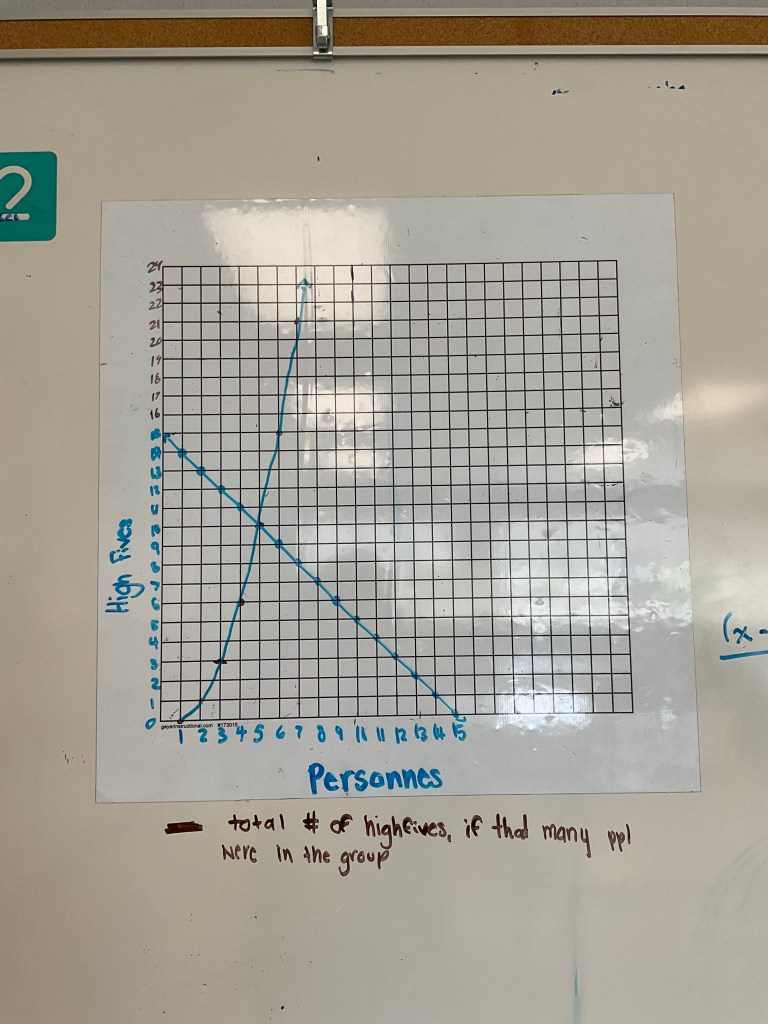
Others were looking for different patterns relating the high fives to the square of x.

It’s fun to look for and explore patterns, and practice expressing them in multiple ways.

Following this task we practiced a bit of modelling of visual patterns, and a few tables. Here’s one where you can model it in standard form, and again in vertex form, depending on how you view it.

We’re getting ready for our culminating task which uses tables to analyse the trajectory of a catapulted pompom. We’re going to be ready!