Building Exponent Models

Today in grade 10 we built exponent models out of toothpicks and plasticine.

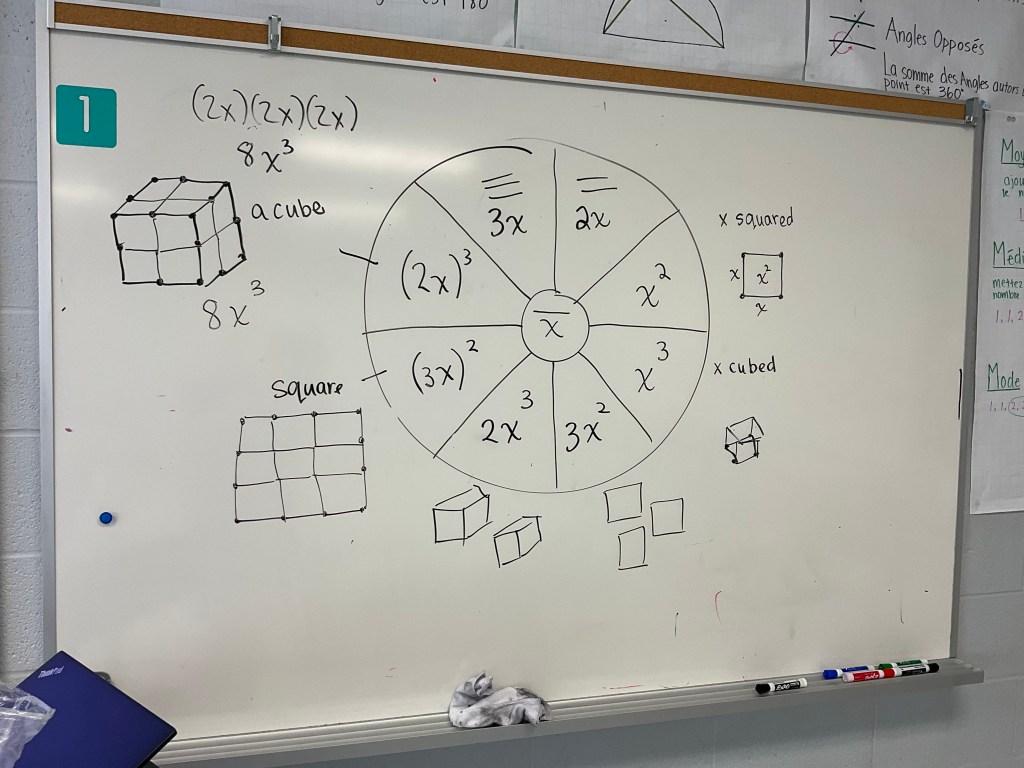
We are working on understanding that anything squared can be physically represented as a square, and anything cubed can be physically represented as a cube.

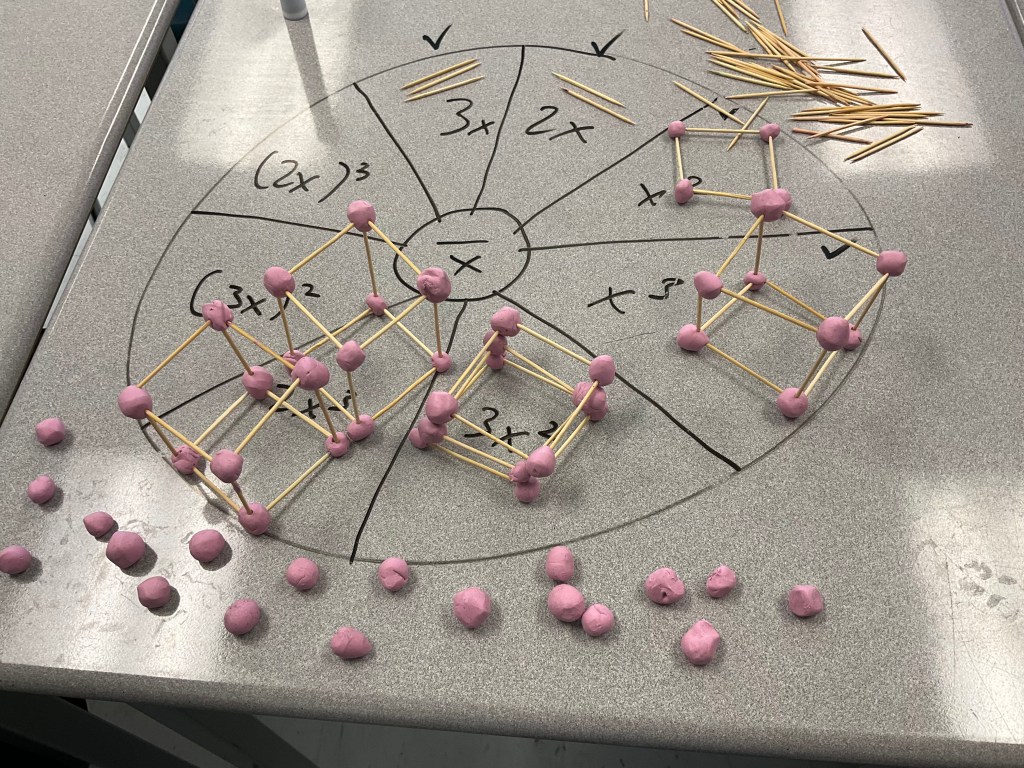
We noticed that the coefficient of the x squared or x cubed tells us how many there are.

If there’s a base that is a bit complicated, like (3x) squared, it means that the side of the square is 3 toothpicks long. That means when we build it we can see that there are 9 little x squareds inside. This means (3x)^2=9x^2

This group made one that wasn’t asked for, the little squares. The base of the exponent in that case would be (1/2 x) and the exponent would be 2 because they are squares. Since they made 4 of them there’d be a coefficient of 4 in front of the expression. We also can see that the 4 put together are equivalent in area to one x squared.

Here’s a good example of (2x)^3, and below there’s an attempt in progress of (3x)^3, which is always a big challenge to build.

We can use this kind of math understanding to help us when we convert square or cube units. Here’s an example: One cubic yard is equal to 27 cubic feet. We can understand this by knowing that there are 3 ft in a yard, and 9 cubic feet on each of the 3 layers of the cube to make 27 cubic feet.

We will be using this knowledge when we do volume and surface area questions in the future.