Knot Tying Task

I was invited to join a grade 10 class today to try out the knot tying task I had done a few weeks ago. This time through it was with an academic class, so we added more algebraic aspects to the investigation.

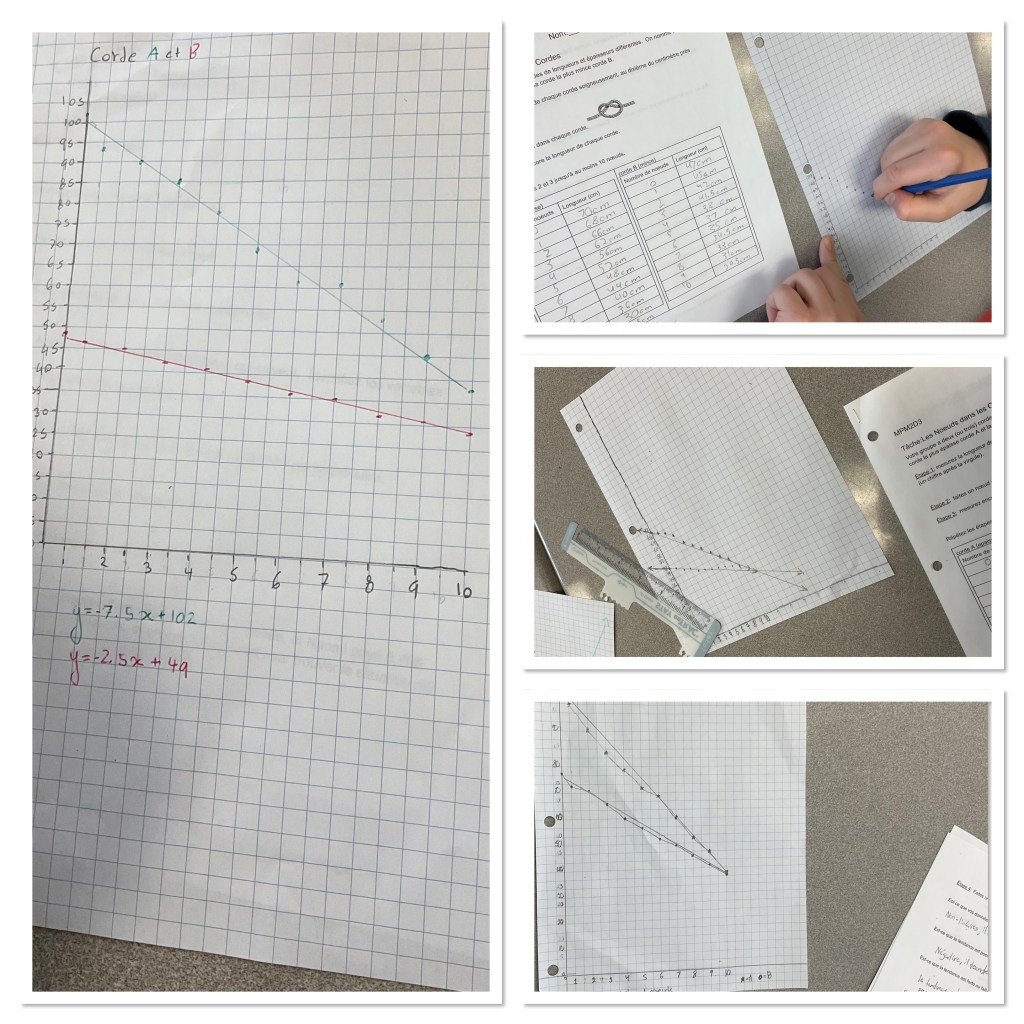
Each group chose 2 ropes. There were longer thicker ropes and shorter thinner ropes and shortest thinnest ropes. They measured the ropes to start with, then tied a knot, then measured, then tied a knot then measured until 10 knots were tied.

They made graphs of their data, made lines of best fit for their data and then made the equations for the lines of best fit.

They needed to determine if there was a number of knots that would make both ropes the same length. This could be solved graphically, but we wanted them to practice their new skill of substitution, so they substituted to solve for the intersection point.

We consolidated in the middle about how to draw a line of best fit, then again a bit later we consolidated how to find the slope and y intercept of this line.

At the end the consolidation mostly focused on what the solution to the system meant, and why it made sense to do substitution. We know that the x represents the number of knots and the y represents the rope length. If we want to know when the ropes are the same length we set the y values equal. That means that the mx+b parts of the equations are also equal. We can solve for the x that makes this true (which represents the number of knots associated with the intersection point). Then we figure out the length of rope associated with that many knots by substituting back into the rope length equation.

It was neat to see lightbulbs go off when students recognized that each knot was shrinking the ropes by approximately the same amount each time, and that the rate of change of the rope length per knot was the slope, and the initial rope length was the y intercept. Having a context to connect the ideas to was really helpful for many students. I look forward to trying this task with another group.