The Most Special Triangles

I had the opportunity to teach a lesson in a colleague’s MCR3U class, a course that I have never taught yet, so it was fun to explore a sequence of steps to learn about special triangles.

Here’s my sequence of prompts.

We noticed that all of the hypotenuse calculations resulted in the side length multiplied by root 2. We noticed that the sine cos and tan of 45 all simplified to be the same, regardless of the side length of the initial square.

We worked through a similar task to develop our next special triangles.

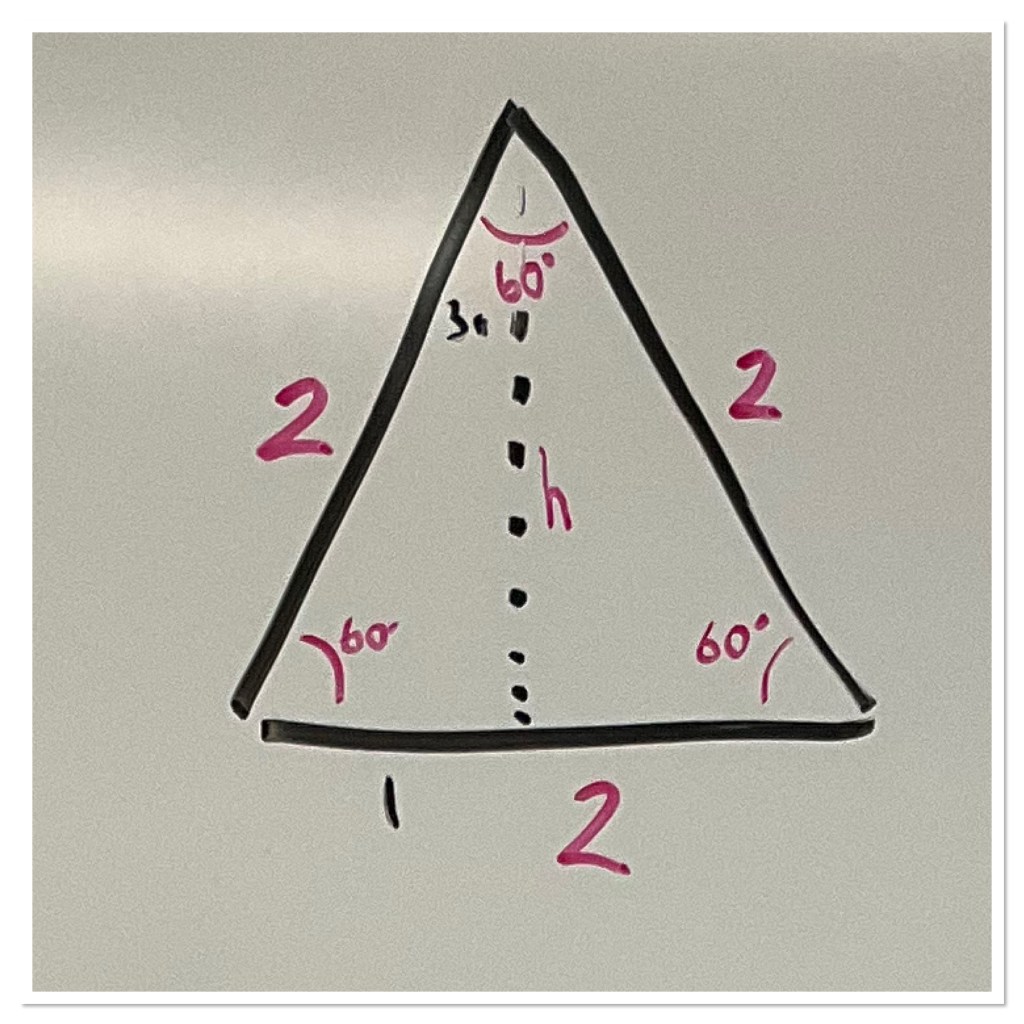
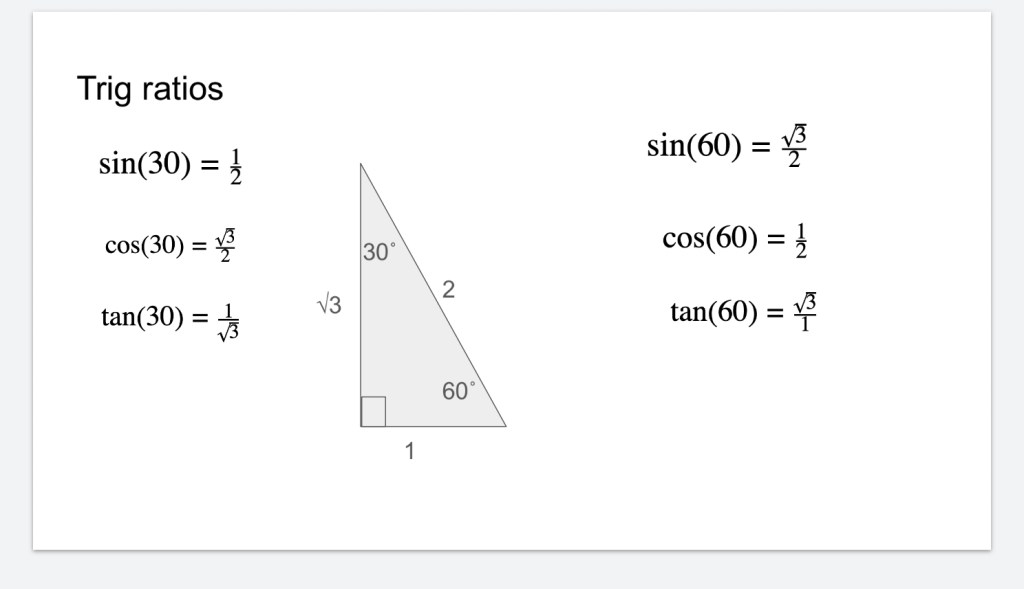
We calculated that the height is root 3. And we see that sin30 and cos60 are the same, and sin60 and cos30 are the same because when the reference angle changes the opposite and adjacent sides now refer to different sides. The adjacent to the 30 degree angle is root 3, and that is the opposite to the 60 degree angle.

Next step was to do a task. This challenge came from Peter Liljedahl’s old website of good problems for teachers.

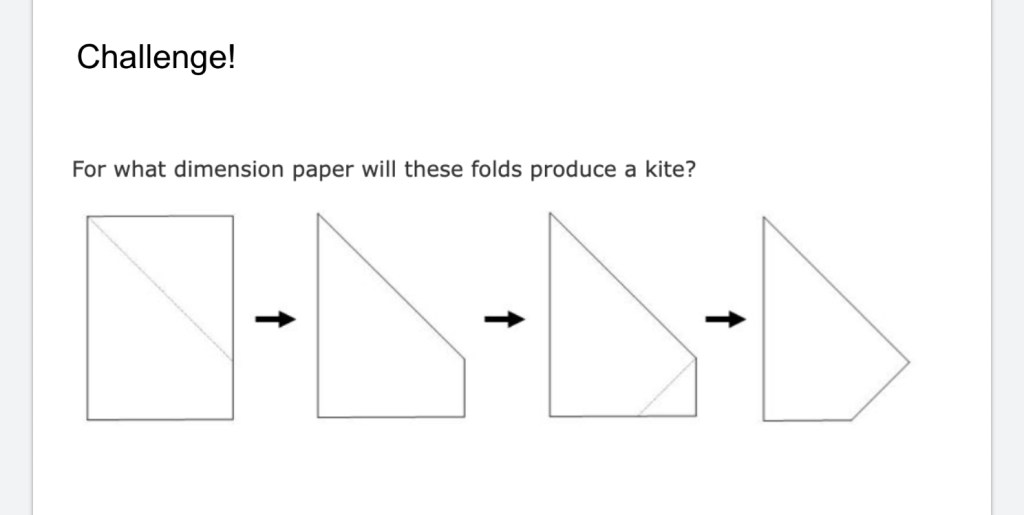
Students worked hard to represent their thinking. We had some physical representation, some calculations of angles and sides, and some use of the new special triangle learning.

It was neat to see which direction various groups took, and whether we all arrived to the same place in the end.