Learning Our Thinking Routines

My grade 9 class learned several thinking routines today. We did a 3 act task, where we started up at the boards in random groups. We did a “notice and wonder” chart as we watched act 1.

We watched it a few times until each group had at least one notice and one wonder.

We debriefed the list of notices and wonders and then set off to determine how many post-its it’d take to finish the picture. Students felt they could do it with the limited information they had, so gave it a good try. I was impressed at their ideas and estimating skills. They weren’t sure of the answers they got, and eventually asked for some more clarifying information.

I wait until students ask for more information to give them the “act 2” material. Here are the dimensions of the post-it and the board.

They got back to work again, figuring out how this information helped. I was purposefully not helpful, hanging back to watch how they tackled the problem, and only coming around to get people to stay on task and stay thinking. There’s a lot of good energy, so I didn’t do much but watch the action unfold.

We gathered to the centre of the room, and I consolidated from the edges, we noticed that most groups drew a diagram and labelled it well. Some groups showed their mathematical thinking, and others only wrote some numbers down before arriving at a conclusion. I added some titles or formatted their numbers to be in equations to show how we can improve our communication, and I also pointed out how some groups solved it by doing area calculations and then dividing, while other groups divided dimensions of the board by dimensions of the post-it and then multiplied those values to find the answer. There were 2 solid approaches, and both were shown.

We sat down and then watched the final act

We had succeeded in our first 3 act task. We will be doing more of these over the term, and the process of getting into groups, up at the boards, noticing and wondering, asking for information, calculating and communicating, and consolidating will get better each time we practice.

We next looked at the thinking routines used for number talks. We did several dot talks today (images from here)

Each of these images were shown for about 3 seconds with the prompt: how many dots are there, and how do you know?

We mostly got the right answer, but that’s not the point. Looking at how we got the answer allowed us to see that different brains process the visual information in different ways. Using the projector markers we outlined how different people viewed the information in different colours, and in the end we saw that we can see things in different ways and that’s cool. Our different approaches can help others see the situation differently as well, so it’s important to share our ideas and viewpoints. We talked about subitizing and also being able to take a visual snapshot and keep it in your head to process when the image is gone, and how those skills can be worked on too.

The final image with the dice led to some conversations about multiplication and how we could represent the process we used to get the answer with algebra. Many did 4×5+4×8, but others did 4×5+4(2×4), and others did 4×8+2×10. Some even saw each dice as a 5 to start since counting by 5 is easy so they did 12(5)-8. Again, it was neat to see different approaches, and also to see how the enthusiasm to share their approach was building in the class.

We looked at the “which one doesn’t belong” routine as well, to spark conversation and get everyone keen to participate.

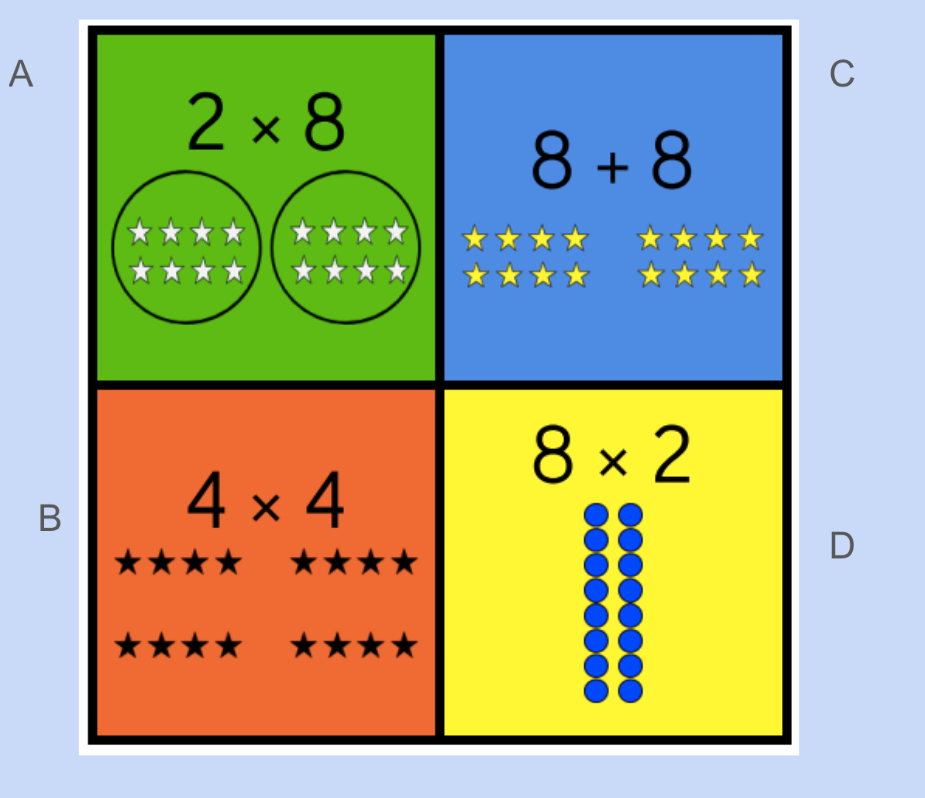
We noticed that there was multiplication and one addition, so maybe corner C didn’t belong. We noticed that each corner had an 8 except corner B, so maybe it didn’t belong. We saw that corner A identified 2 distinct groups, in circles, so maybe A didn’t belong, and that corner D has an array, and also we’re counting circles not stars, so maybe D doesn’t belong. There are reasons for each corner to not belong, and we can debrief ideas like “groups of” and repeated addition and multiplication and arrays. We had a lot of participation in the thinking and sharing of ideas, which led to lots of participation in our next number talk: “how many eggs”?

These talks are not so much about the answer, but about how we get there, and appreciating and sharing our thinking. Some immediately saw an array 4×9, but others said they counted groups of 8 (4×2 seen vertically) and there are 4.5 groups of them. I took the opportunity to show the skill of “doubling and halving” and how we could double the 4.5 and halve the 8 and arrive at the 4×9 multiplication as well. Others were keen to show how they counted by 2s, or counted by 4s, or how they subdivided it into 3 dozens. (2×6), (2×6) and (3×4) which again was lovely as a way to see how arrays of 12 can have different dimensions. As we debriefed, I was trying to touch on some multiplication fluency, as we will be embedding fluency as we proceed most days when we can.

Finally, since there was some time left, we got back to the boards and did the 4 4s challenge. Using only 4 copies of a number 4, and all the mathematical operations, and any exponents, and brackets, we were trying to create expressions that have a value of 1,2,3,4,5,6.7,8,9,10. I started them off with 4+4-4-4 as my example of how to get 0.

We had so many great conversations about if brackets are needed, and where to put them. Students were talking about BEDMAS before I got the chance! I love it when that happens. I just need to echo their “bedmas” realizations out loud to the class when I hear it as they work at the walls, and then so many memories are jogged, and they are all discussing what order to write things, or where to place brackets.

In the final moments of class (I am amazed at how much we covered) there was time for one of my favourite songs.

What an earworm!

Looking forward to more fun tomorrow. We’re building the routines we will use all term. So far it’s going great!