Inverse Functions

Today my grade 11s were working on inverses of functions. The activity requires a single hole punch, and some creative folding. Here it is to download if interested. I was inspired by a post on social media which I have now misplaced.

Step 1 was to draw the line y=x

Step 2 was to fold along the line y=x

Step 3 was to use the hole punches to make holes along the given function.

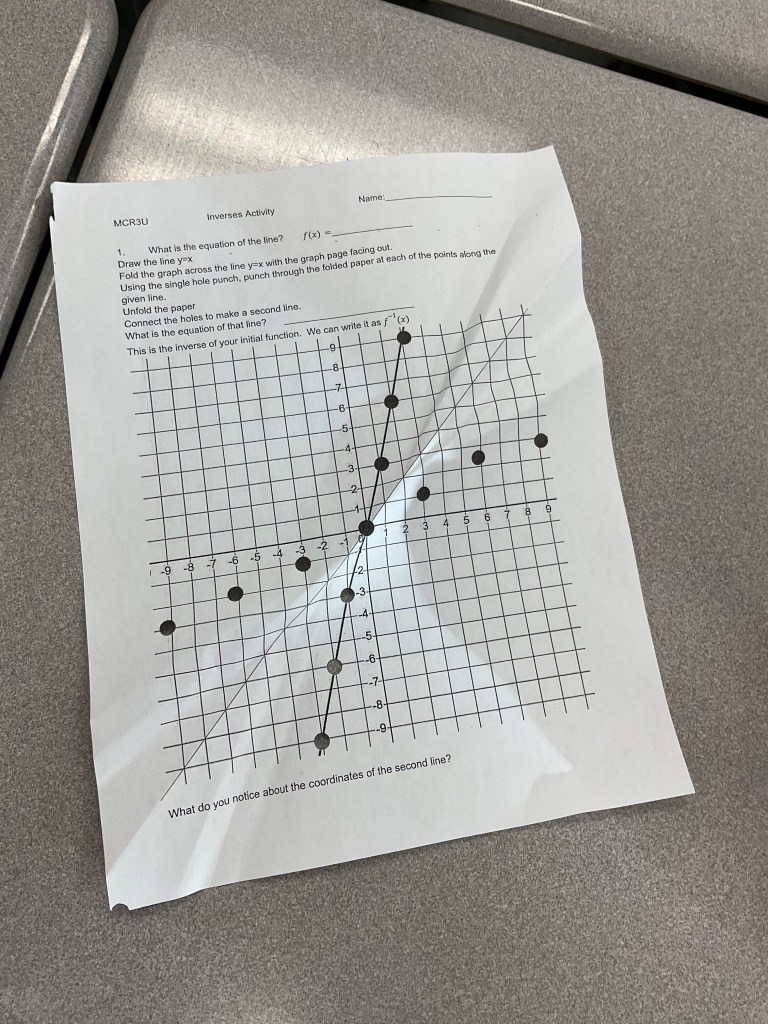
Step 4 was to join up the new dots to make a different line/curve.

We were able to debrief a lot of things through this task. We saw that the lines have coordinates thar have reversed values, e.g. (1,3) will correspond to (3,1) on the new graph. The two are also reflected across the line y=x. We can also see that the first line has a slope of 3 and a constant of 0 so the output is input times 3. For the 2nd graph the slope is 1/3 and the constant is 0 so the output is input times 1/3 or input divided by 3.

We can see how the function and its inverse will undo each other. The operations of times by 3 and divide by 3 are inverses. If the output of the function is used as the input of the inverse you’d get the initial input back again.

We needed some creative folding to get the hole punch to reach the dots sometimes.

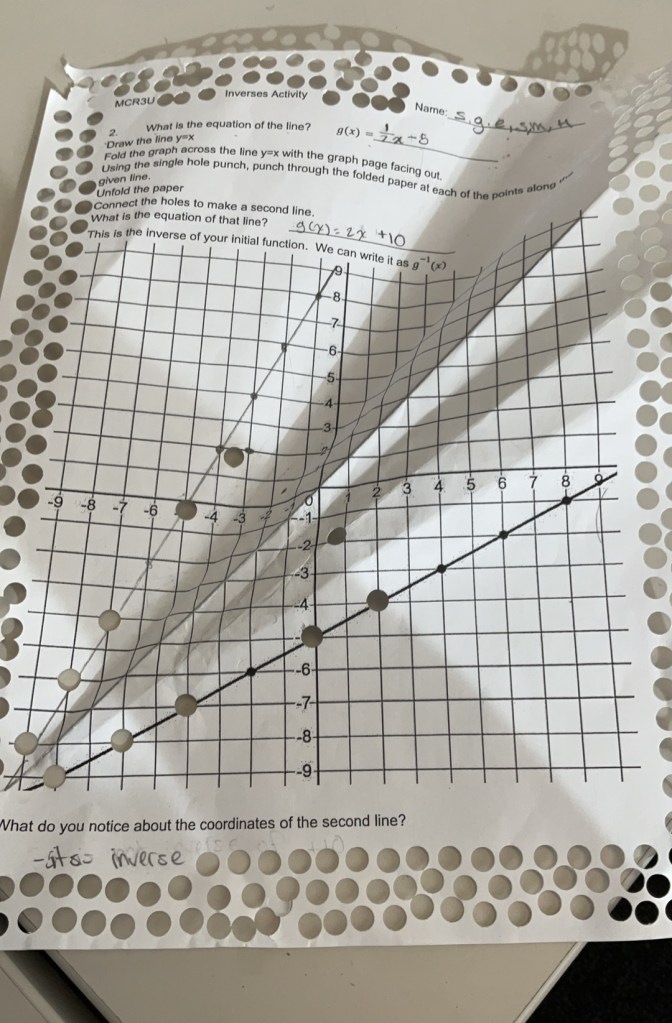
This one has a function of y=1/2x-5 and the inverse is y=2x+10

we were able to switch x and y in the function and then by using opposite operations we could isolate the y. Y=2(x+5) which is the same as the inverse if we expand.

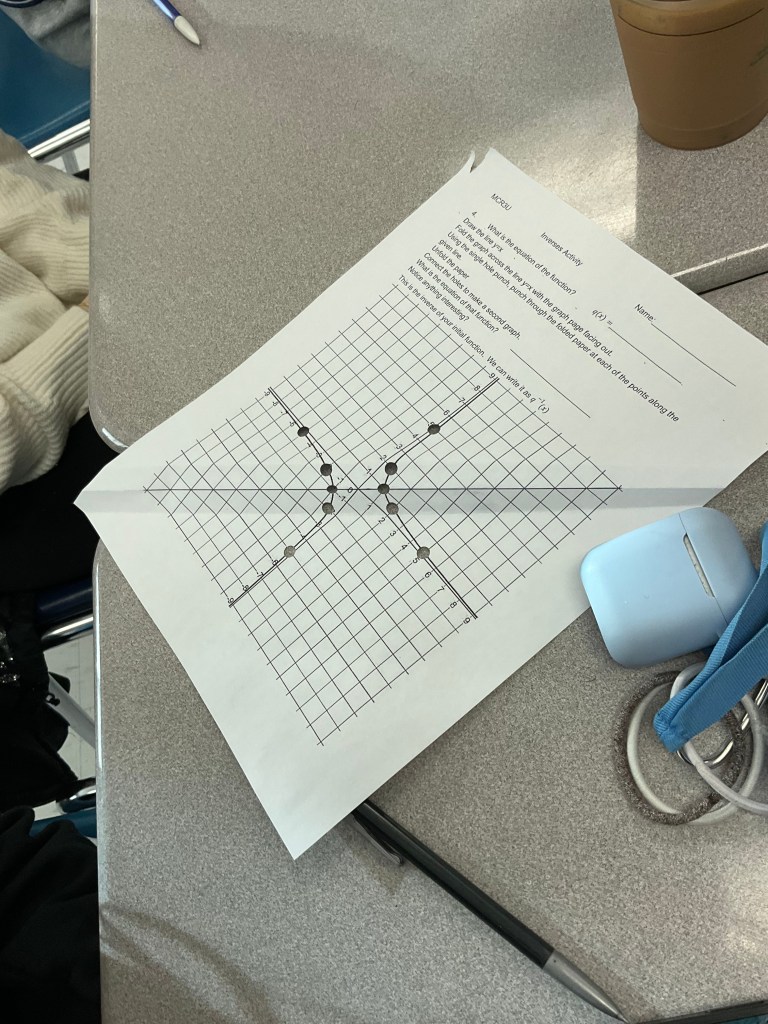
We saw that some functions are their own inverses. We showed how that works with algebra.

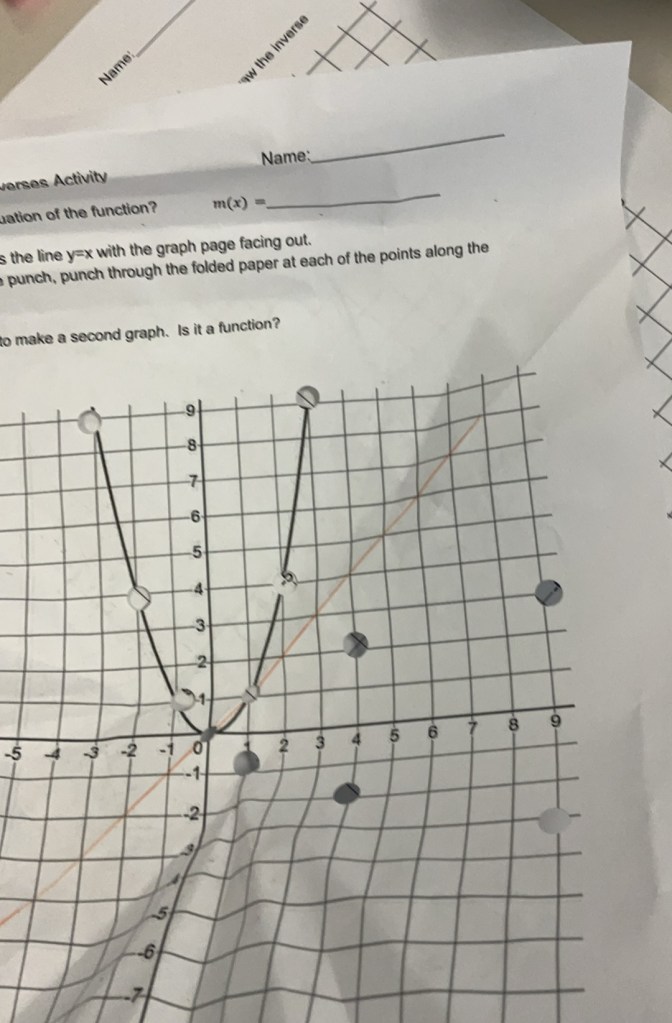
We also saw how this function is not invertible. If we follow the process we don’t get a function in the end. The original function needs to pass the horizontal line test for it to be invertible. We can restrict the domain of the function to make it invertible.

I think we have laid the groundwork conceptually, visually, and algebraically and we will be able to practice more as the course continues.