Volume of Pyramids and Cones

Today we looked at the volume of pyramids and cones, and developed the formulae using water.

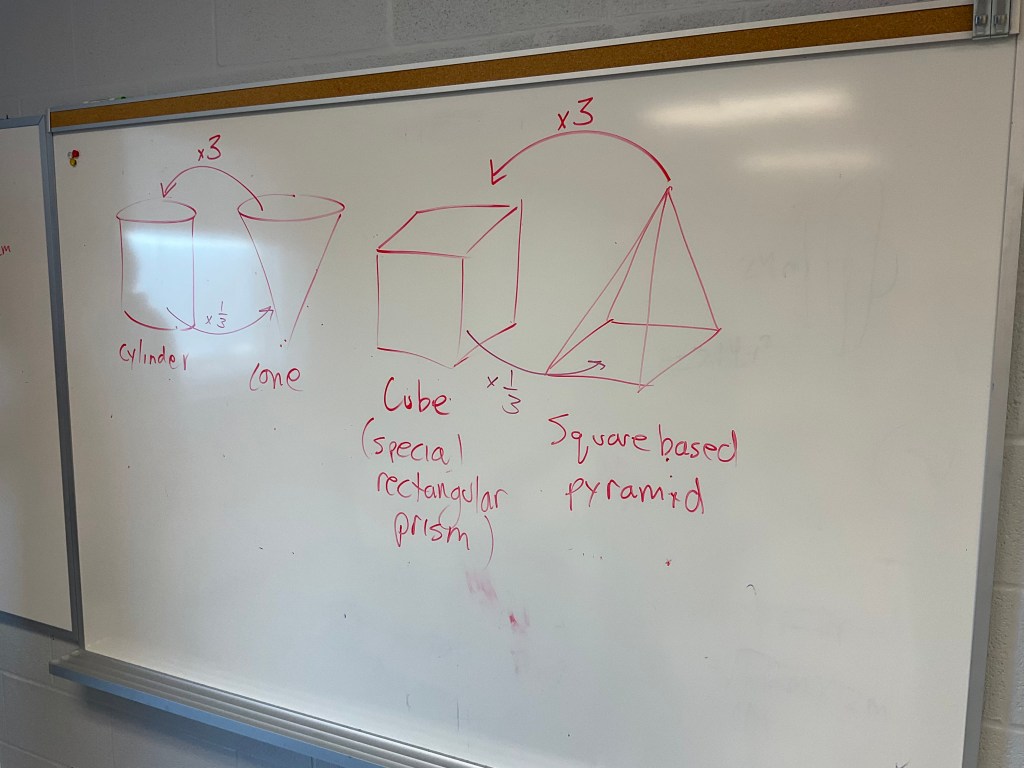
By using the geometric solids we discussed the properties of prisms and pyramids, and then guessed how many cones it would take to fill a cylinder with the same base and height. Many students guessed 2, 2.5, 3, 4 as possibilities. After the cone was filled once, and dumped into the cylinder, students were prompted to look at it and refine their guess if needed. Most converged on an idea of 2.5 or 3ish.

Finally, everyone could see that it took 3 cones to exactly fill the cylinder to the top. The same process was repeated for square based pyramids and a square based prism, and then again for a triangle based prism and triangle based pyramid.

In the end, students saw that it took exactly 3 pyramids to fill a prism with the same base and height. (Note: if you are doing this activity be very careful not to overfill the pyramids since a meniscus would affect the volume).

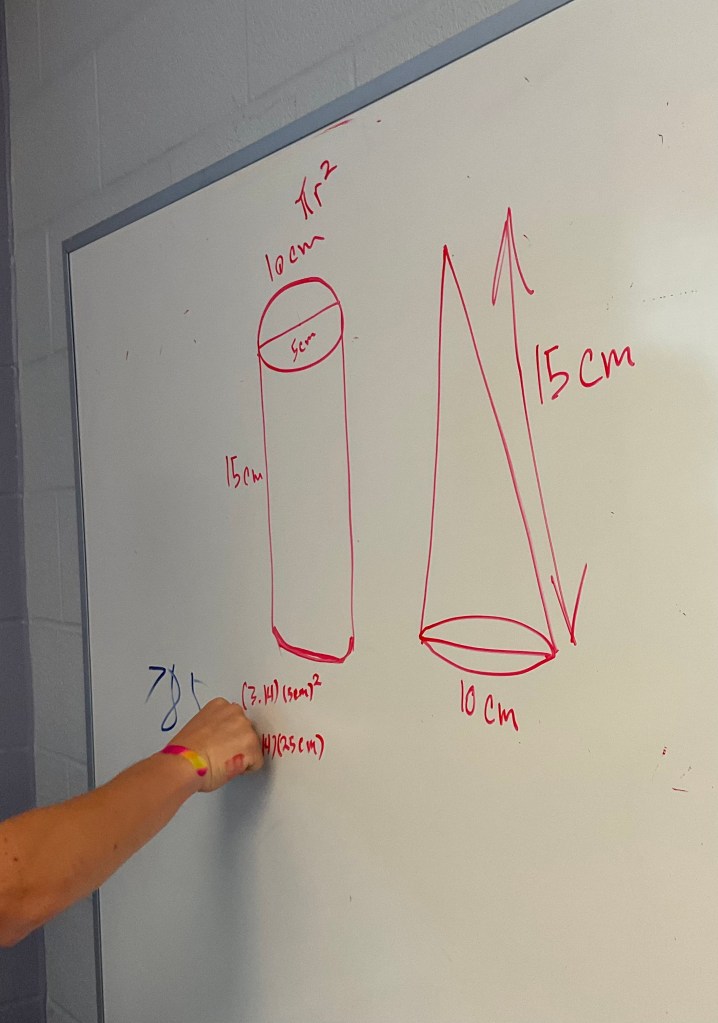
Next, the idea of working backwards from cylinder to cone means that we multiply by 1/3. A cone contains 1/3 of the water that the cylinder did.

From there, students were up at the boards in small groups working on calculating the volume of pyramids and cones, and cylinders and prisms.