Math Club For Grown Ups

We had our 3rd meeting of our math club for grown ups. Many thanks to all who attended and enthusiastically solved (or attempted) problems together.

We looked at 3 problems. The first was sourced by one of our students who needed a good challenge after their work was complete one day. We were led by a colleague who prompted us to think about our feelings as we were faced with this challenge.

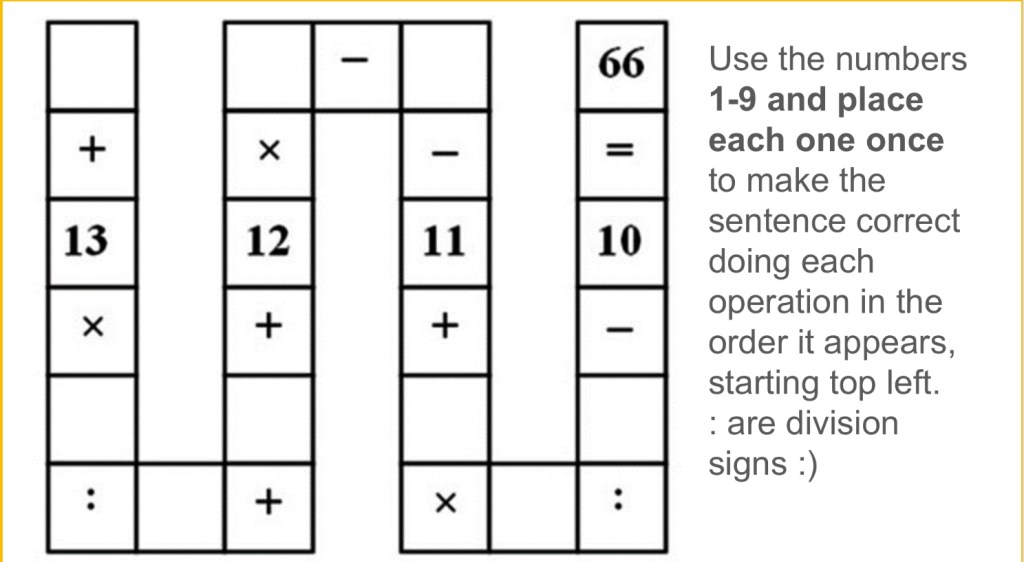
We worked at it in small random groups for quite a while. I know that my group struggled with where to start, and if to work forwards or backwards, and we kept getting confused because we were instructed to NOT use BEDMAS which is hard.

We took a pause after about 30 minutes of struggle, and during that moment where we were considering our feelings, one of our groups solved it! (Spoilers ahead)

We next tackled the pirate question from Peter Liljedahl’s site.

We took time to explore the problem, and figure out how to keep track of our data and how to extend the patterns that we saw. Some groups didn’t want to start with 10 pirates, they started with a smaller case of 4 or 5 or 6, which in this case doesn’t clarify the situation as much as might be hoped. One group started off with a general case of n pirates which is quite an overwhelming task.

We made good progress, and left with people who were worried they’d wake in the night with new solution ideas!

The final task we looked at is how to use cup stacking in grade 9, 10, and 11/12 math as a way to explore and model linear, quadratic and cubic patterns.
Cups stacked in a single tower are a great linear model. Cups can be stacked from a desk to get a “b” value. If the cups are stacked in a nested fashion from the desk, and an upright/inverted fashion from the floor, you get a linear system that could be solved.

If cups are stacked in a triangle, it’s a quadratic model. Some good prompts would be: “How many cups are needed to make a triangle stack that’s a meter tall?” or “as tall as me?” or “how tall of a triangle stack could you make with 300 cups?”
The modelling could be done by hand for a 2D class or with desmos (there’s a nice regression button available now) for a 2P class.

If the stack is a pyramid (either square or triangle based) the model is cubic. This would be a good question for grade 11/12 functions or advanced functions to explore by hand and confirm with desmos.

It’s fun to be able to see and feel the model that you are making. There’s more sense making when you can see that there are so many more cups needed to make an additional row in quadratics compared to linear, and even more when using a cubic model.

I can see extensions where a cubic, quadratic, and linear model are all explored, looking for intersections. Different types of stacks could be built starting on desks or shelves or the floor to include different vertical translations.

I also brought in paper cups which are exactly half of the red cups (total fluke), but it brings about a nice conversation about the vertical transformation that occurs. The graph has a vertical compression, because each cup is half, so the entire stack would be half the height of the stack made with the red cups. I look forward to the chance to try this with my next sr. math class.