Thinking about Factoring
In grade 10 today we were looking at what value of “k” would make expressions factorable.
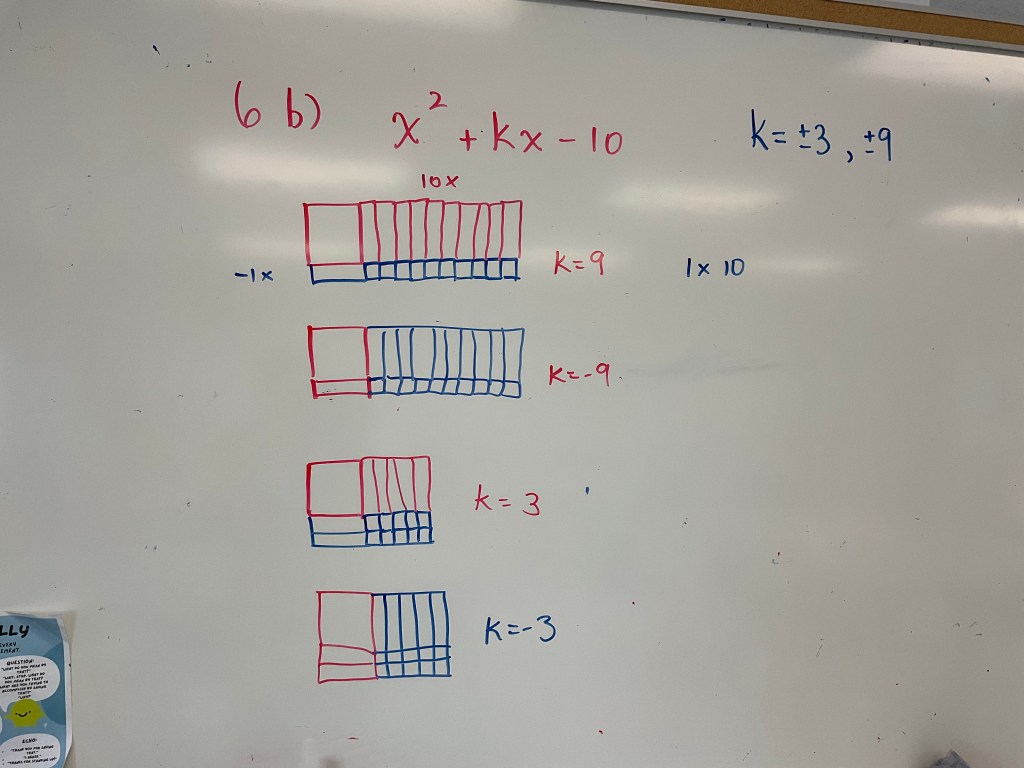
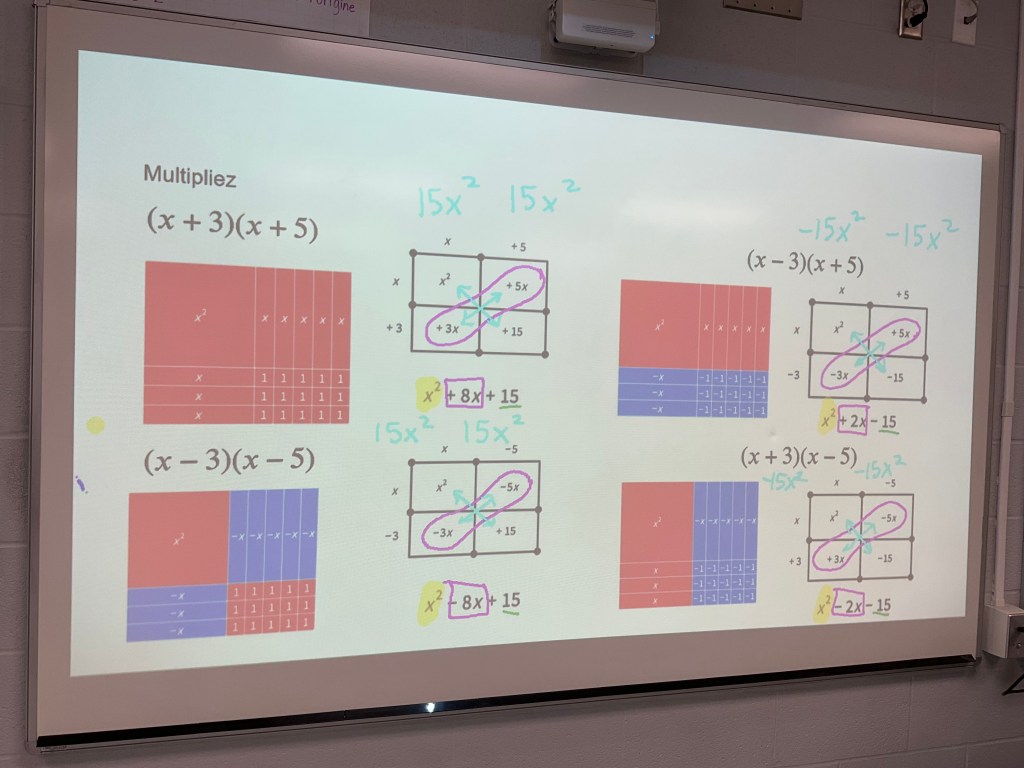
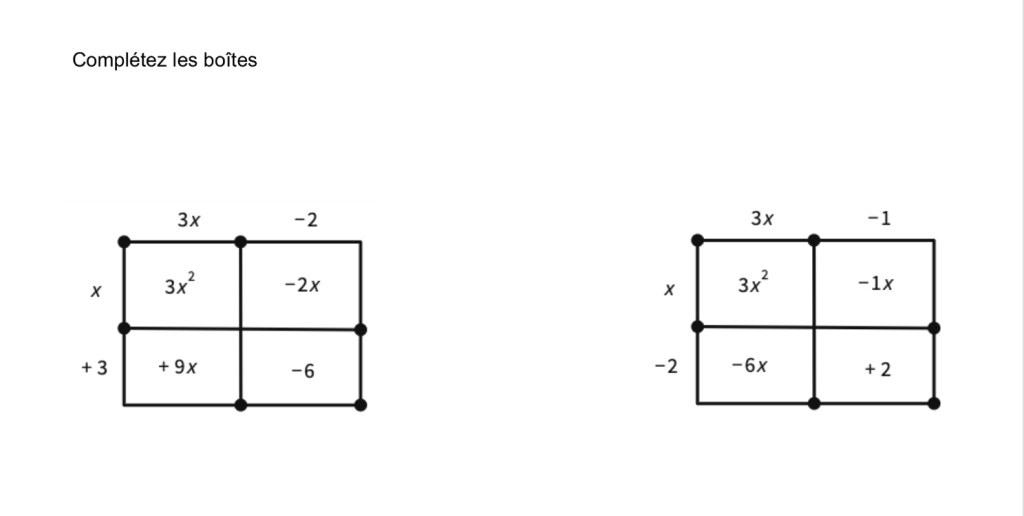
We used our logic and understanding of algebra tiles to build all the rectangles we could. We can change the number of x tiles we have, that’s all.
After working through several examples, we looked at a mix of factoring questions.
We’re getting much better with practice! We need to work on identifying cases where we need to factor, then factor again.
Fractions Boot Camp Day 2
Today was a short class, but we worked on representing and comparing fractions using relational rods. We had a concept diagram, with a 1 being defined as 12 units long (a 10 rod and 2 1 rods). Students worked to represent each fraction in the wheel by comparing the lengths to the central fraction as a help.
We recognized that the numerator was the number of pieces we needed, and the denominator was the number of pieces that equalled the “1”.
We noticed that some of the fractions were equivalent lengths!
we had some groups wanting to try to do something similar with the pattern blocks, so we tried a different concept circle with that group.
At the end of class we looked a little bit at adding fractions together using the fraction strips.
we looked at writing fraction equivalents 2/3=4/6, and 7/3=14/6 etc.
we looked at questions like 1/3+5/6 and realized we needed to make the pieces all the same size before we could count them up. If we wrote 1/3 as 2/6 then we could add up 2/6 and 5/6 and get 7/6.
more concept circles to come tomorrow!
Intro to Factoring (box method)
We know that when we multiply binomials using the area model we will have like terms appear on the diagonal. We notice that these two terms add up to give us the central term in the trinomial. We noticed today that the diagonals in both directions have the same product. We can use these discoveries to help us work backwards.
when we fill in the boxes we multiply. When we are looking for the dimensions on the outside of the box we need to common factor. For example, the bottom row has -6x and +2 we can common factor a -2 from both terms. We place the -2 on the outside of the box, and then can fill in the dimensions at the top of the box, 3x and -1, and then the other dimension missing on the vertical side would be x. The dimensions are in total (3x-1)(x-2). The solutions are below.
We worked hard at the walls in groups to use the area model to expand and also to factor. We are going to keep working on these skills moving forward.
Fraction Boot Camp Day 1
I’m helping out for a few days with a GLS class who are working on deepening their fractions understanding and skills. Our goal is to use as many different concrete representations as we can.
We started off by creating unit fractions, by folding various strips of paper into equal sized pieces. We had some challenges with the 1/3, 1/5 and 1/10.
We noticed that the more folds made, the smaller the segments. That means that the bigger the denominator the smaller the unit fraction.
We noticed that there were a few ways to make 1/2. We can say that 3/6, or 2/4 or 4/8 or 5/10 all equal 1/2.
Our next job was to put these unit fractions on a number line. We could use the folded pieces as a ruler to help us out.
Our next challenge was to use the digits 0,1,2,3,4,5 as numerators for fractions with denominators of 2,3,4,6,8, and to create fractions to add to the number line.
We noticed that if you make fractions that have the same numerator and denominator the fraction simplifies to 1. We know 3/3 and 4/4 are equal to 1 and easy to put on our number line. We also know that if the numerator is 0 the fraction simplifies to 0.
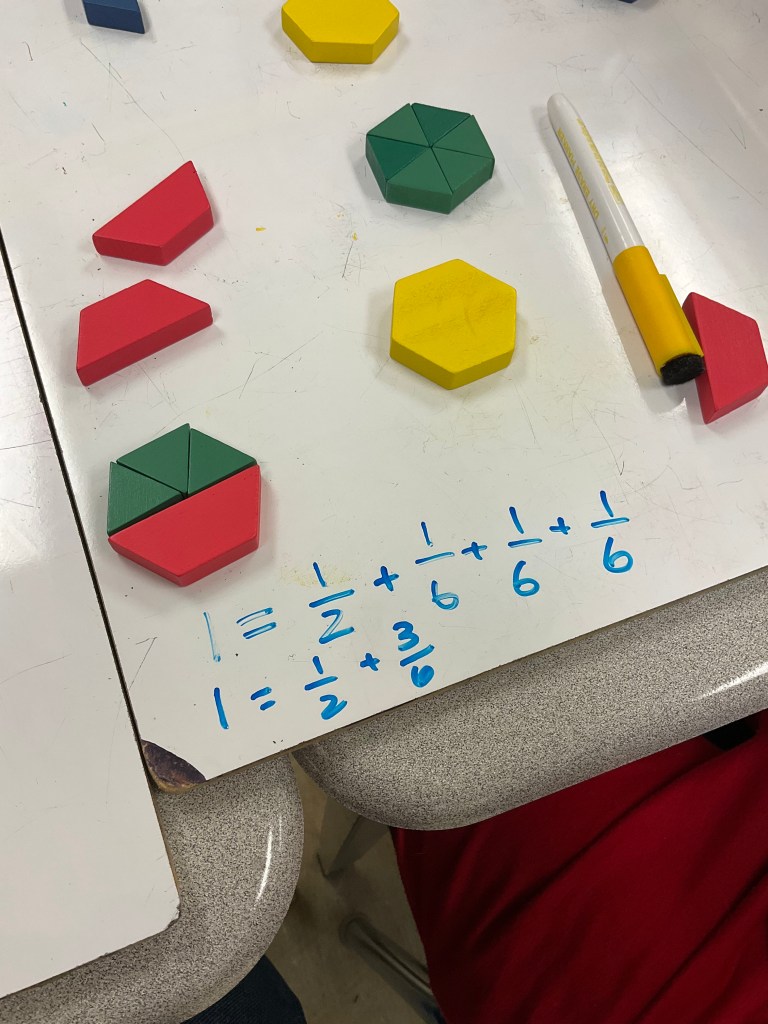
We used pattern blocks to represent fractions as well. We know that 1 hexagon can be created using 1 red block and 3 green blocks. Each red block is 1/2 a hexagon and each green block is 1/6th of a hexagon. We can write that 1=1/2+1/6+1/6+1/6
Tomorrow we will use a few new tools to represent and compare fractions.
Connecting Representations
We’ve been practicing how to model quadratic visual patterns for a while now, looking at different strategies (tables, graphs, equations, and visual representations). Here’s an example of a practice problem.
we had 2 different equations that worked based on how we viewed the pattern.
We had a summative task this week where students were exploring 2 different patterns, and comparing the equations of area and perimeter and using the patterns to solve various problems. It was in the middle of prompting a student that I had the idea to suggest using algebra tiles to build figure x to help the student visualize what’s going on.
I’m not sure why I hadn’t considered this earlier, we use tiles all the time for lots of things! This moment changed how I will approach the scaffolding of the patterning tasks. Where I used to ask students to extend the patterning to figure 4, and then back to figure 0 (to determine the constant). I’ll now ask them after the drawing of figure 4 to construct figure x from tiles. With the representation in tiles the area and perimeter equations are so easy to determine.
It’s great to make connections between representations, and to find even more ways to use the tools that we have.
Solving Problems
We are working on solving word problems and making equations. We have so many strategies to try! Some groups enjoy making tables of values, but it’s hard to get the correct exact answer.
other groups modelled with equations and graphs
one group dove right in and used substitution, and showed that they knew that they got it right by verifying their solution.
Introduction to Substitution
We are starting substitution in MPM2D. We used a visual task to start.
4 acrobats and 5 grandmothers are tied in a tug of war.
A dog is now tied with 2 grandmothers and an acrobat.
we need to figure out which side will win the final round.
We worked in random groups up at the boards to make sense of the situations, and represent our thinking and our logic. I enjoy this problem as it allows multiple approaches, and there is usually at least one group that will “discover” the algebraic approach of substitution.
we had groups work on representing their data and organizing it in tables, and creating equations.
one group decided to say that 1 grandmother was the base unit of strength, and that an acrobat was 1.25 times the grandmother’s strength since 5 grandmothers=4 acrobats. They determined that a dog was 3.25 times the strength of a grandmother, then decided that the side with the dog would win.
this group decided that since 4x=5y that they could relate this to 20=20 so x would be 5 and y would be 4. They then calculated that the dog would be 14, and then they substituted values to decide that the side with the dog would win.
Here is what one group did, substituting the value of (1a+2g) in place of d, and then using that to solve.
We will be using substitution a lot moving forward. It was good to have such enthusiastic participation on day 1.
Algebra Tiles for Expanding and Factoring
In grade 10 we’re working on expanding and factoring quadratic expressions using algebra tiles.
We make rectangles out of the tiles, such that long sides touch long sides and short sides touch short sides. The tiles used are x^2+7x+12, and the dimensions are (x+3) and (x+4)
Since length x width = area, we can write (x+3)(x+4)=x^2+7x+12
We can start out with an area 2x^2-x-1 and build a rectangle using tiles. We need to add some zero pairs to fill out the rectangle. The dimensions will be (x-1) and (2x+1), so we know that (x-1)(2x+1)=2x^2-x-1
We are working in building understanding of multiplication and factoring, first with tiles, and then later we will use the area model to expand and factor.
Introduction to Substitution
This is a task from 50 Problem-solving Lessons Grades 1-6 by Marilyn Burns Math Solutions Press 2003, which helps introduce the idea of substitution in a less algebraic way. There is a tug of war competition between 4 acrobats and 5 grandmas and they are tied.
In round 2 a dog is tied when pulling against 2 grandmas and an acrobat
In round 3 we do not know who will win. We have 3 grandmas and a dog against 4 acrobats. We need figure out, and justify who will win.
Students were split up into small groups at the boards. They needed to figure out who would win round 3, and justify it.
some did beautiful work with sentences, explaining their thinking and logic.
others started to make equations and expressions using variables
Some got quite wound up in equations, but their solution was not easy to navigate without a map!
Others decided to make all of the relationships in terms of one variable, and use that to solve. They related 4m=5w so m=1.5w, and did the same for a dog d=w+w+m turns into d=3.25w.
There was a unique approach that I had never seen before. This group went from the equation 4A=5G and decided to place a value for A and G by relating it to an equation of 100=100 (since 100 can be divided by 4 and 5), so then A would be 25 and G would be 20
It was impressive to see the skills students were bringing to grade 10, and how they were working hard on communicating their thinking. The typical approach to solve this problem would be to substitute 2 grandmas and an acrobat in the place of a dog, and then to compare from that point. We can physically understand substituting 2 grandmas and an acrobat instead of a dog because of their same pulling force. This can help build the understanding of substituting equivalent expressions as a way to reduce the number of variables in use in a problem.
Perimeter and Area task
I visited a MTH1W class as they were working on perimeter and area concepts. They plotted their names and calculated the perimeter and area of their names. It’s a good review of the differences between perimeter and area, before moving on to look at other composite shapes.
Ms. Bearse's Site 