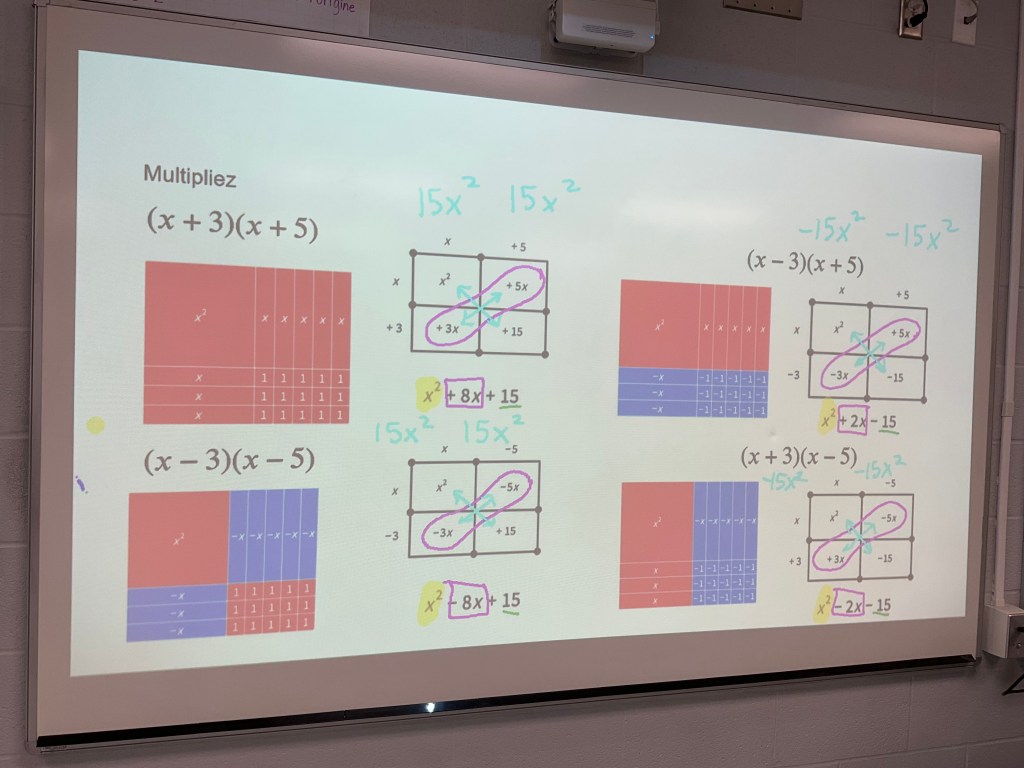
Paper Folding Fractions
I was working this morning with an MAT1L class who started a unit on fractions. The goal I set was to do a lot of work with unit fractions. We started by doing paper folding, which was quite challenging for some to get equal pieces.
We made connections that the more pieces we make, the smaller the size of the pieces, so the bigger the denominator the smaller the unit fraction.
We put the unit fractions on a number line.
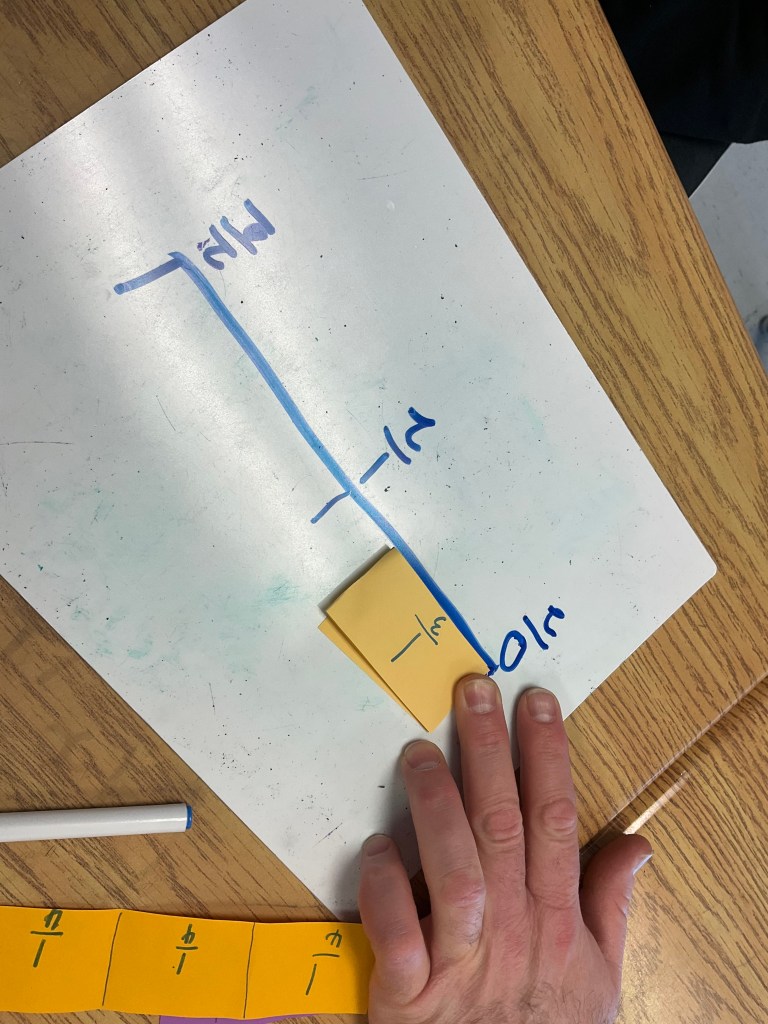
Some students put a lot of fractions on their number line. Once they have well folded unit fractions they can really get a sense of comparison between fractions.
We looked at adding up unit fractions including what happens if we make improper fractions. There was some hesitation from the students to deal with anything larger than five one fifths. We had spent so much time living in the zone between 0 and 1 so this is understandable. We were able to show that 5 one fifths add up to 1, and then we’d have 2/5 left over so we have a mixed number 1 and 2/5.
I look forward to coming back later this week to explore more fraction fun with this class.
Concept Circles for Fractions
Today in MAT1L I got to help with concept circles to explore fractions.
We used the 100 as our unit, and then had some segments of the concept circles had fractions, and some had handfuls of tiles. Students were working on writing the fraction, or building the fraction with the blocks.
We were working on counting by hundredths and also by tenths. We have some work to do, but it was a good start.
Graphing Parabolas
We graphed parabolas today for the first time. I gave an equation in factored form, y=(x-1)(x-3) and then we set out to make tables of values to see what it looked like.
Some students worked from the factored form as given, and others decided to expand first and use the trinomial.
We looked for patterns in the tables of values, noticing that the 2nd differences are the same, and also that there is symmetry in the y values.
We graphed another one: y=(x+2)(x+4) and noticed some interesting trends when we looked at both equations and graphs.
We made the connection that the numbers in the brackets are related to the x intercepts, and that the low point is always in between the x intercepts, exactly in the middle.
We looked at how the x intercept values make zero pairs with the expressions in brackets. We saw how the midpoint calculations from earlier in the course will come in handy to find the middle, between the x intercepts, and how we can substitute that value into the equation to find out where the vertex will be.
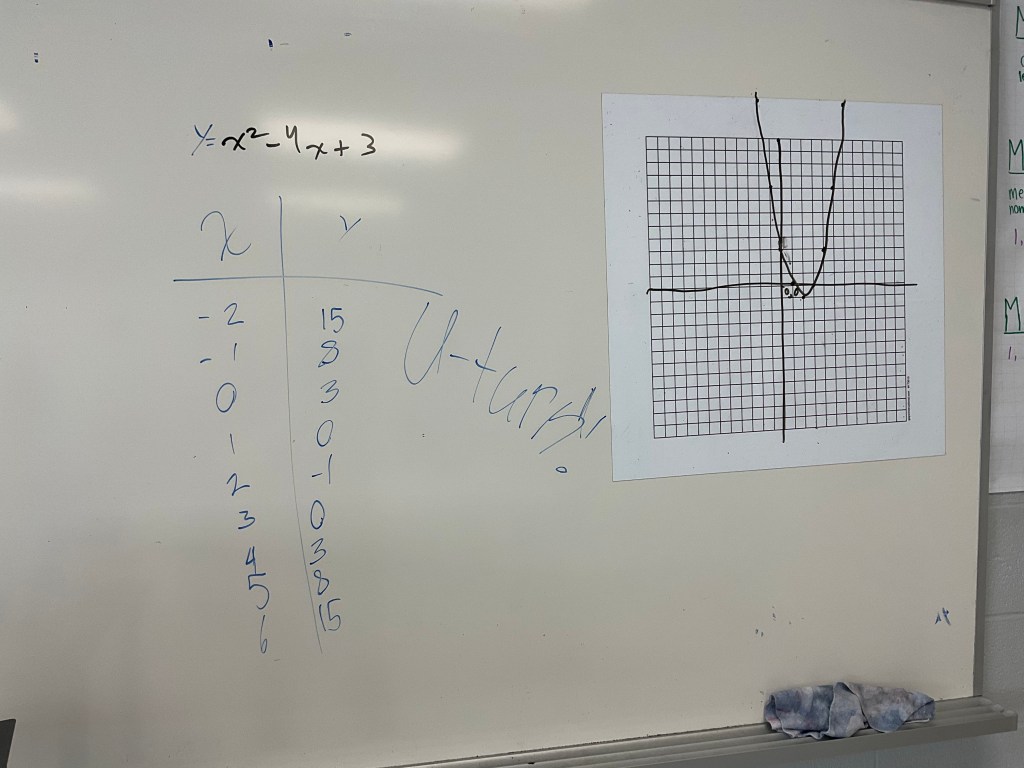
We noticed that there’s only one “u turn” in these graphs. We look forward to doing more practice with this tomorrow, and connecting our factoring skills to helping us graph parabolas.
Fraction Boot Camp Day 3
Today in our fraction boot camp we looked at visual representations of fractions
We started with a number talk looking at what fraction is shaded. There is lots to talk about in this one image. There were 3 different shaded regions that we looked at.
Next we looked at the unusual baker’s cakes problem, with this image. We stated that the cakes are all sold for 60 dollars, and our task is to determine what each piece should be sold for.
There was a lot of good discussion among groups, and good representations shown on the boards. We’ve realized that there’s lots of ways to draw fourths and halves, as triangles or rectangles.
The next task was a circuit of concept circles where fractions were represented by money, lego, pattern blocks, and base 10 blocks.
After 3 days of fractions we’re feeling kind of fractionned out, but hopefully also we’re a bit more confident with using manipulatives to represent fractions to solve problems.
Thinking about Factoring
In grade 10 today we were looking at what value of “k” would make expressions factorable.
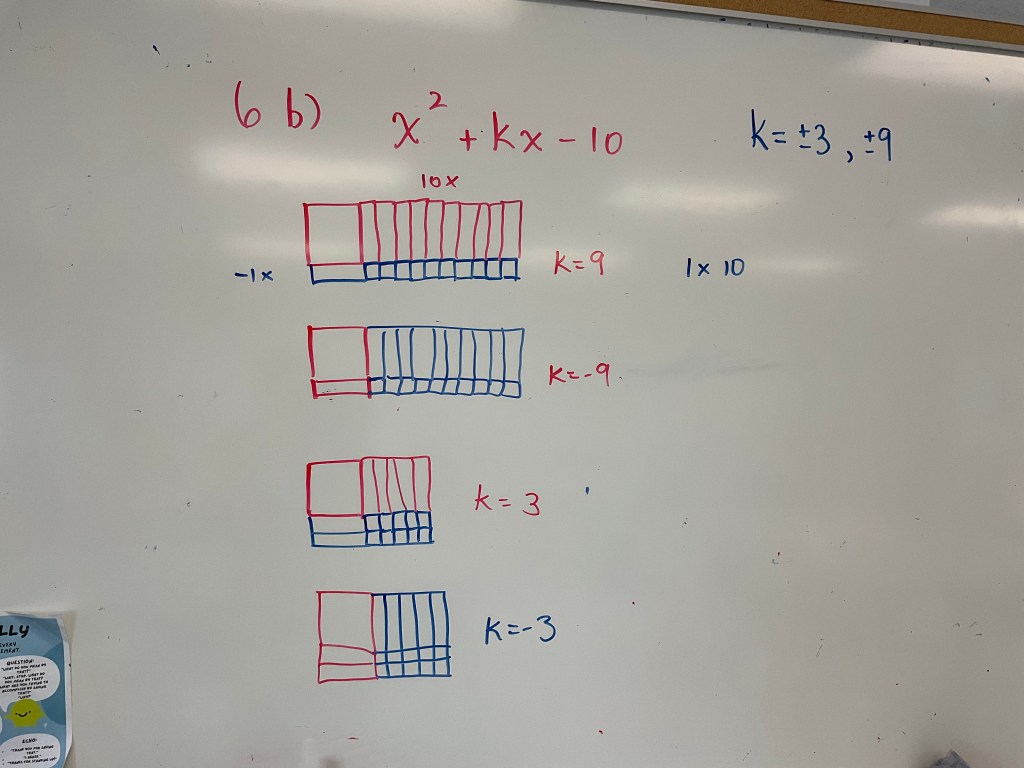
We used our logic and understanding of algebra tiles to build all the rectangles we could. We can change the number of x tiles we have, that’s all.
After working through several examples, we looked at a mix of factoring questions.
We’re getting much better with practice! We need to work on identifying cases where we need to factor, then factor again.
Fractions Boot Camp Day 2
Today was a short class, but we worked on representing and comparing fractions using relational rods. We had a concept diagram, with a 1 being defined as 12 units long (a 10 rod and 2 1 rods). Students worked to represent each fraction in the wheel by comparing the lengths to the central fraction as a help.
We recognized that the numerator was the number of pieces we needed, and the denominator was the number of pieces that equalled the “1”.
We noticed that some of the fractions were equivalent lengths!
we had some groups wanting to try to do something similar with the pattern blocks, so we tried a different concept circle with that group.
At the end of class we looked a little bit at adding fractions together using the fraction strips.
we looked at writing fraction equivalents 2/3=4/6, and 7/3=14/6 etc.
we looked at questions like 1/3+5/6 and realized we needed to make the pieces all the same size before we could count them up. If we wrote 1/3 as 2/6 then we could add up 2/6 and 5/6 and get 7/6.
more concept circles to come tomorrow!
Intro to Factoring (box method)
We know that when we multiply binomials using the area model we will have like terms appear on the diagonal. We notice that these two terms add up to give us the central term in the trinomial. We noticed today that the diagonals in both directions have the same product. We can use these discoveries to help us work backwards.
when we fill in the boxes we multiply. When we are looking for the dimensions on the outside of the box we need to common factor. For example, the bottom row has -6x and +2 we can common factor a -2 from both terms. We place the -2 on the outside of the box, and then can fill in the dimensions at the top of the box, 3x and -1, and then the other dimension missing on the vertical side would be x. The dimensions are in total (3x-1)(x-2). The solutions are below.
We worked hard at the walls in groups to use the area model to expand and also to factor. We are going to keep working on these skills moving forward.
Fraction Boot Camp Day 1
I’m helping out for a few days with a GLS class who are working on deepening their fractions understanding and skills. Our goal is to use as many different concrete representations as we can.
We started off by creating unit fractions, by folding various strips of paper into equal sized pieces. We had some challenges with the 1/3, 1/5 and 1/10.
We noticed that the more folds made, the smaller the segments. That means that the bigger the denominator the smaller the unit fraction.
We noticed that there were a few ways to make 1/2. We can say that 3/6, or 2/4 or 4/8 or 5/10 all equal 1/2.
Our next job was to put these unit fractions on a number line. We could use the folded pieces as a ruler to help us out.
Our next challenge was to use the digits 0,1,2,3,4,5 as numerators for fractions with denominators of 2,3,4,6,8, and to create fractions to add to the number line.
We noticed that if you make fractions that have the same numerator and denominator the fraction simplifies to 1. We know 3/3 and 4/4 are equal to 1 and easy to put on our number line. We also know that if the numerator is 0 the fraction simplifies to 0.
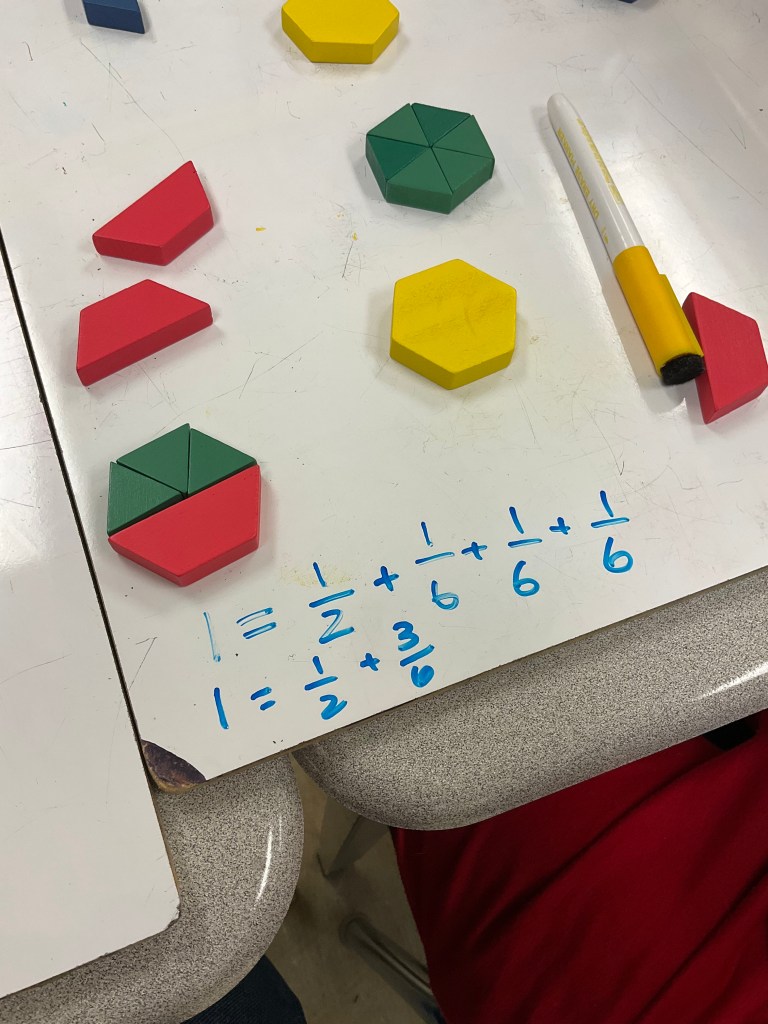
We used pattern blocks to represent fractions as well. We know that 1 hexagon can be created using 1 red block and 3 green blocks. Each red block is 1/2 a hexagon and each green block is 1/6th of a hexagon. We can write that 1=1/2+1/6+1/6+1/6
Tomorrow we will use a few new tools to represent and compare fractions.
Connecting Representations
We’ve been practicing how to model quadratic visual patterns for a while now, looking at different strategies (tables, graphs, equations, and visual representations). Here’s an example of a practice problem.
we had 2 different equations that worked based on how we viewed the pattern.
We had a summative task this week where students were exploring 2 different patterns, and comparing the equations of area and perimeter and using the patterns to solve various problems. It was in the middle of prompting a student that I had the idea to suggest using algebra tiles to build figure x to help the student visualize what’s going on.
I’m not sure why I hadn’t considered this earlier, we use tiles all the time for lots of things! This moment changed how I will approach the scaffolding of the patterning tasks. Where I used to ask students to extend the patterning to figure 4, and then back to figure 0 (to determine the constant). I’ll now ask them after the drawing of figure 4 to construct figure x from tiles. With the representation in tiles the area and perimeter equations are so easy to determine.
It’s great to make connections between representations, and to find even more ways to use the tools that we have.
Solving Problems
We are working on solving word problems and making equations. We have so many strategies to try! Some groups enjoy making tables of values, but it’s hard to get the correct exact answer.
other groups modelled with equations and graphs
one group dove right in and used substitution, and showed that they knew that they got it right by verifying their solution.
Ms. Bearse's Site 