Introduction to Substitution
We are starting substitution in MPM2D. We used a visual task to start.
4 acrobats and 5 grandmothers are tied in a tug of war.
A dog is now tied with 2 grandmothers and an acrobat.
we need to figure out which side will win the final round.
We worked in random groups up at the boards to make sense of the situations, and represent our thinking and our logic. I enjoy this problem as it allows multiple approaches, and there is usually at least one group that will “discover” the algebraic approach of substitution.
we had groups work on representing their data and organizing it in tables, and creating equations.
one group decided to say that 1 grandmother was the base unit of strength, and that an acrobat was 1.25 times the grandmother’s strength since 5 grandmothers=4 acrobats. They determined that a dog was 3.25 times the strength of a grandmother, then decided that the side with the dog would win.
this group decided that since 4x=5y that they could relate this to 20=20 so x would be 5 and y would be 4. They then calculated that the dog would be 14, and then they substituted values to decide that the side with the dog would win.
Here is what one group did, substituting the value of (1a+2g) in place of d, and then using that to solve.
We will be using substitution a lot moving forward. It was good to have such enthusiastic participation on day 1.
Algebra Tiles for Expanding and Factoring
In grade 10 we’re working on expanding and factoring quadratic expressions using algebra tiles.
We make rectangles out of the tiles, such that long sides touch long sides and short sides touch short sides. The tiles used are x^2+7x+12, and the dimensions are (x+3) and (x+4)
Since length x width = area, we can write (x+3)(x+4)=x^2+7x+12
We can start out with an area 2x^2-x-1 and build a rectangle using tiles. We need to add some zero pairs to fill out the rectangle. The dimensions will be (x-1) and (2x+1), so we know that (x-1)(2x+1)=2x^2-x-1
We are working in building understanding of multiplication and factoring, first with tiles, and then later we will use the area model to expand and factor.
Introduction to Substitution
This is a task from 50 Problem-solving Lessons Grades 1-6 by Marilyn Burns Math Solutions Press 2003, which helps introduce the idea of substitution in a less algebraic way. There is a tug of war competition between 4 acrobats and 5 grandmas and they are tied.
In round 2 a dog is tied when pulling against 2 grandmas and an acrobat
In round 3 we do not know who will win. We have 3 grandmas and a dog against 4 acrobats. We need figure out, and justify who will win.
Students were split up into small groups at the boards. They needed to figure out who would win round 3, and justify it.
some did beautiful work with sentences, explaining their thinking and logic.
others started to make equations and expressions using variables
Some got quite wound up in equations, but their solution was not easy to navigate without a map!
Others decided to make all of the relationships in terms of one variable, and use that to solve. They related 4m=5w so m=1.5w, and did the same for a dog d=w+w+m turns into d=3.25w.
There was a unique approach that I had never seen before. This group went from the equation 4A=5G and decided to place a value for A and G by relating it to an equation of 100=100 (since 100 can be divided by 4 and 5), so then A would be 25 and G would be 20
It was impressive to see the skills students were bringing to grade 10, and how they were working hard on communicating their thinking. The typical approach to solve this problem would be to substitute 2 grandmas and an acrobat in the place of a dog, and then to compare from that point. We can physically understand substituting 2 grandmas and an acrobat instead of a dog because of their same pulling force. This can help build the understanding of substituting equivalent expressions as a way to reduce the number of variables in use in a problem.
Perimeter and Area task
I visited a MTH1W class as they were working on perimeter and area concepts. They plotted their names and calculated the perimeter and area of their names. It’s a good review of the differences between perimeter and area, before moving on to look at other composite shapes.
Visual Patterns
We started a new semester today, and we hit the ground running in grade 10.
we continued the pattern, made tables of values and equations, and figured out how many’d be in figure 13.
We worked at the boards in small random groupings, sharing a marker, and working together on these tasks.
Some students saw this and ignored the colours. They saw a large square and a small square overlapping.
The larger square is (x+1)^2, and the smaller square is x^2, and they overlap, so they overcount the 1 square that is contained in both, so that’s why there’s a subtract 1 at the end.
others used the table of values to find the common 2nd difference of 4. We had already see that this is double of the “a” value. We can see that the constant is 0, so the next step is to calculate the b value.
A potentially easier way to find the equation is visually. We see in figure 3, when x is 3, there are two 3×3 squares, in other words, 2x^2, and there are also 2 groups of 3 (2 groups of x) remaining. The equation is y=2x^2+2x.
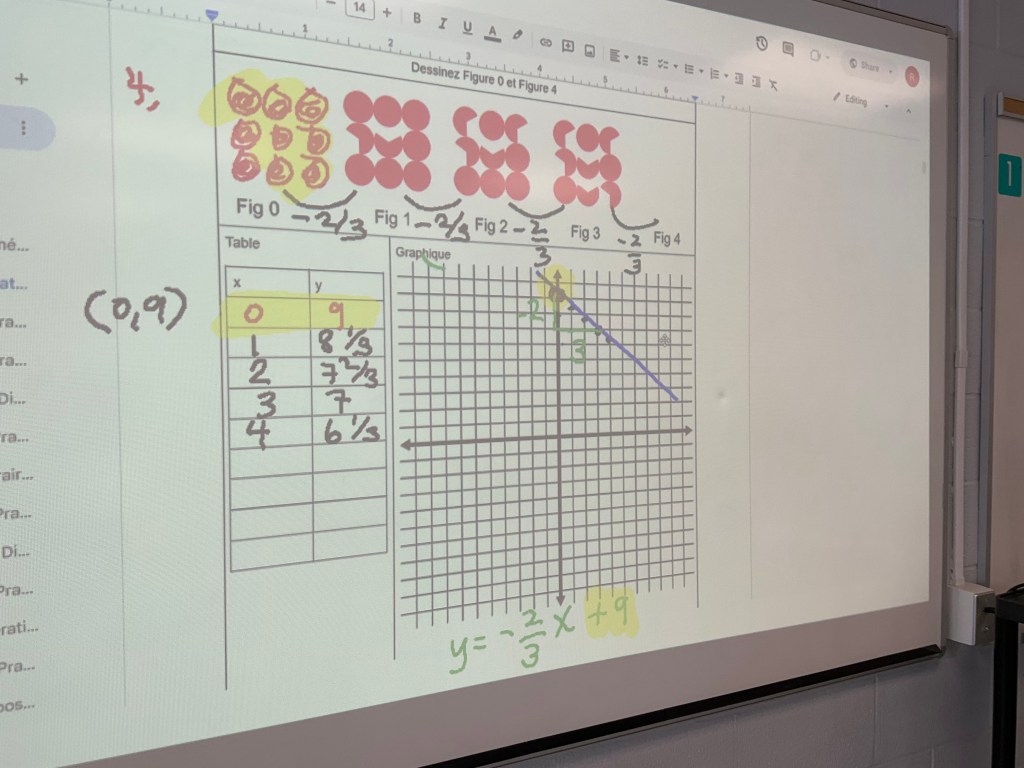
We also had a look at what linear patterns look like (this is a review from grade 9). Our goal was to make a table, graph, and equation for patterns presented. Some patterns were linear, and some quadratic.
We worked on our math skills and our groupwork skills, and have a little bit of practice to do tonight.
well done grade 10s! A good start to a new semester.
EQAO day 1
Grade 9s worked really hard today on the first part of their provincial testing. Tomorrow is day 2.
Monopoly
Today in MAT1L students were preparing for their exit interviews, and some who were done interviews played monopoly with me!
We had good conversations about making change, and adding and subtracting, and if it’s a good idea to buy things if we don’t have a lot of money.
Professional Development Session
I was honoured to lead a professional development session with our in-house feeder school. We looked at various ways to use manipulatives in math class.
We made a concept circle to show various representations with money.
A similar strategy can be used with base 10 blocks to represent integers
We can change what’s in he middle as well and look at fractions decimals and percents
We then used toothpicks and plasticine to build models of exponents, and see how x squared, x cubed, and x are all very different and can’t be added or subtracted.
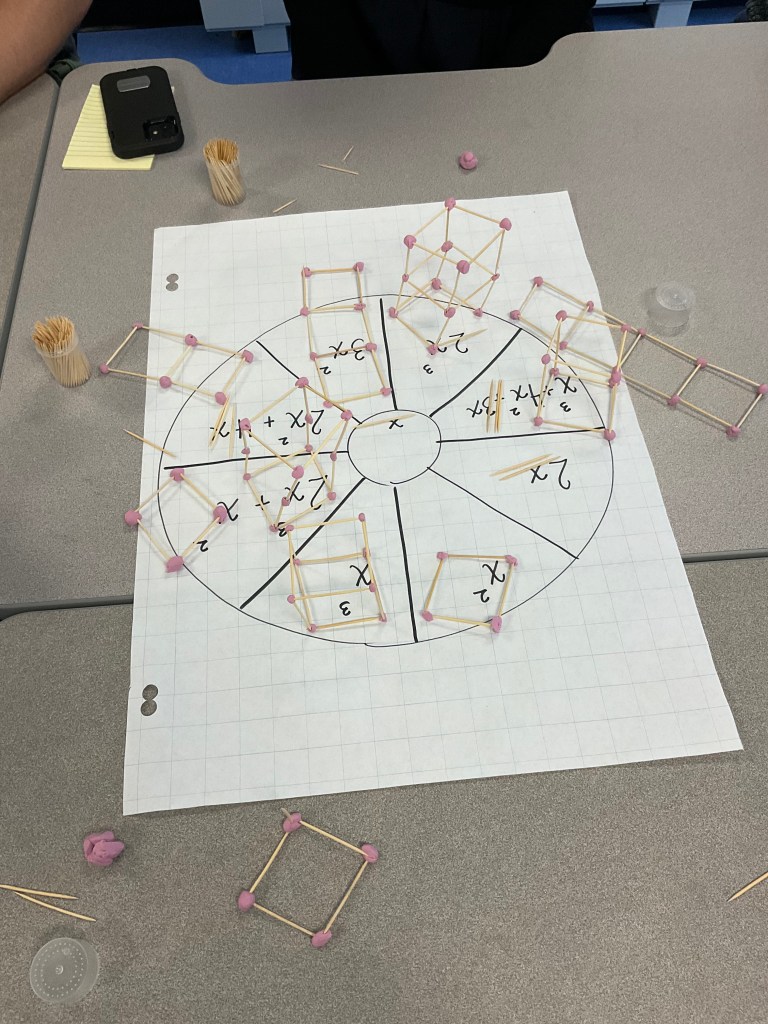
next we introduced algebra tiles as another way to show algebra.
we took a bit of time and worked with tiles and the “bucket of zeros” for adding and subtracting and multiplying integers. Then we also spent time using tiles ro solve equations.
my presentation is listed in the professional development tab on this site if you want to see more! It was a pleasure working with such enthusiastic educators. We look forward to doing something similar next term with our other local feeder schools.
Catapult Culminating
In grade 10 we’ve been working though our culminating task where we build catapults to launch pompoms.
We use the app Visual Physics to help us analyse the trajectory of the launch.
We can identify the axes, the scale, and then locate the pompom over time.
The data can then be interpreted with another app, which can pull the data points into a table of values, and/or a graph which can be smoothed.
Students then determine the vertex, the x intercepts, the y intercept from the table and the graph, and use this to answer questions like where should a target be placed, or if the catapult is launching from a chair or a desk of different height, where should the target be located on the floor.
Exploring Sine Law
Grade 10s today had a look at relationships in triangles. We measured sides and angles as accurately as we could, and then we looked at ratios.
We compared the ratios of sinA/a and cosA/a and tanA/a and the same for B and C. We noticed a lot of things when we looked at the values.
we noticed that tangent is the only ratio that can have values greater than 1. We looked at why that could be the case. Sine and cosine are ratios of opposite and hypotenuse, and adjacent and hypotenuse. The hypotenuse (always the longest side) is always the denominator, so the fraction will be between 0 and 1 when divided. Tangent compares opposite and adjacent, and sometimes the adjacent is the big side, and sometimes the opposite is the big side, so tangent can be any value from 0 to infinity.
We also noticed that the ratios of sinA/a=sinB/b=sinC/c, and we formalized that this is the sine law. We then started using it to solve problems with non-right angle triangles.
Ms. Bearse's Site 