Solving Systems By Graphing
I had the pleasure to be in a MTH1W class that was working on solving systems of equations with tables and by graphing.

In small random groups students tackled the problem with many strategies. Some made equations, then graphed directly. Some groups rewrote 1.5 as 3/2 to show the slope in a fraction form to help graph more easily.

Some made tables and equations and graphs which all showed that there’s a cross over point, or point of intersection at 4km and $11.

A follow up question was regarding the planning of a birthday party. At Tony’s Pizza they charge $150 for the party room and $12 per guest, and at Joey’s Hamburger it costs $180 for the party room and $10 per guest.
Some groups made equations, then used tables and calculated values until they could see a cross over point.

Groups that tried to graph directly from equations had a struggle with the scales, and plotting rise and run accurately. Lines started to look almost parallel, even though we know that the rates are not the same. The point of intersection would be way off the graph in this case.

Student are getting confident applying their skills to solve problems with linear equations, and to work together in groups and communicate their learning.
Building Pyramids and Confronting Misconceptions
We’ve had 2 inclement weather days to start the week. It threw off our schedule a bit, and caused us to do some tasks in a different way. This allows for some interesting observations.
First of all, each class can react very differently to a given task depending on many factors (personalities, willingness to take risks, time of day), so these observations may be based on many factors.
Usually I do a day 1 task of “build me a rectangular prism with a volume of 300 cubic centimetres”. This allows students to have an introduction to building things, working in groups on an open task, and reminds them of volume calculations from their prior learning.
Because of timing, students did some work on the inclement weather days on volume and surface area of prisms, and then today we started our building task.
After watching and participating in the demo with water
The challenge is then given to build a square based pyramid with a volume of 300 cubic centimetres. Groups flocked to whiteboards to plan, and it was interesting to see what aspects were challenges.

After some productive struggle the connection was made between the water demo and the task. The volume of a prism with same base and height would be 900 cubic centimetres. Many groups drew on the work on the whiteboards for inspiration, and there were lots of pyramids with sides of the base that were 6cm. They knew that (36)(25)=900, and they took the square root of the 36 to get the side lengths of the square. They then decided to take the square root of the 25 to get side lengths of the triangles, which was an interesting misconception that took off around the room.

We had some groups make their pyramids and bring them to me for verification. They were adorable pyramids, but did not have the correct volume.

Groups were sent back to the drawing board to make the volume bigger, with sides of the base being 6cm and the height of the pyramid as 25cm.

Eventually we had some that were closer. These were just a bit short though! The students measured the desired height of the pyramid as the height of each triangle, which causes the pyramid to be too short. This can be remedied by using the Pythagorean theorem to calculate the slant height of the pyramid, as shown with the pipe cleaners on the wireframe model.
Other groups had some unique ideas for dimensions: this one had a base of 9.65 cm by 9.65 cm and a height of 9.65cm. They needed a Pythagorean adjustment to make theirs work in the end. It was neat that they used the cube root of 900 to get their dimensions.

Here’s another that found a new misconception. They made the base of the pyramid 10cm by 10cm and then measured the side of the triangle as 9cm. It was much shorter than they had anticipated, and went back to the drawingboard to make it taller.

Some groups were able to confront their misconceptions and rebuild, and other groups had major issues with even starting the task once. There is something to be said about struggling through an iterative design process! This task has never taken this many turns before, and it makes me wonder whether it was the fact that they didn’t build prisms the day before, or whether it was first period back after a weekend prolonged by 2 snow days.
Courageously Solving Equations with Fractions
We summoned our courage on a Friday afternoon and worked on solving equations with fractions in MTH1W.

We worked up from solving equations without fractions, to equations like x/2=4, where we understand that the fraction just means x is divided by 2 and the answer is 4. We can undo that division by 2 by doubling each side.
Next we looked at solving equations with binomial numerators like (x-3)/2=4, and we used the same strategy of doubling each side as a first step to solve.
We then looked at solving equations with variables on both sides like (x+5)/4=3x
Next we looked at questions with fractions on both sides, and variables on both sides. We now needed a new strategy of “make a common denominator” and then we can multiply both sides by that denominator to get rid of it.
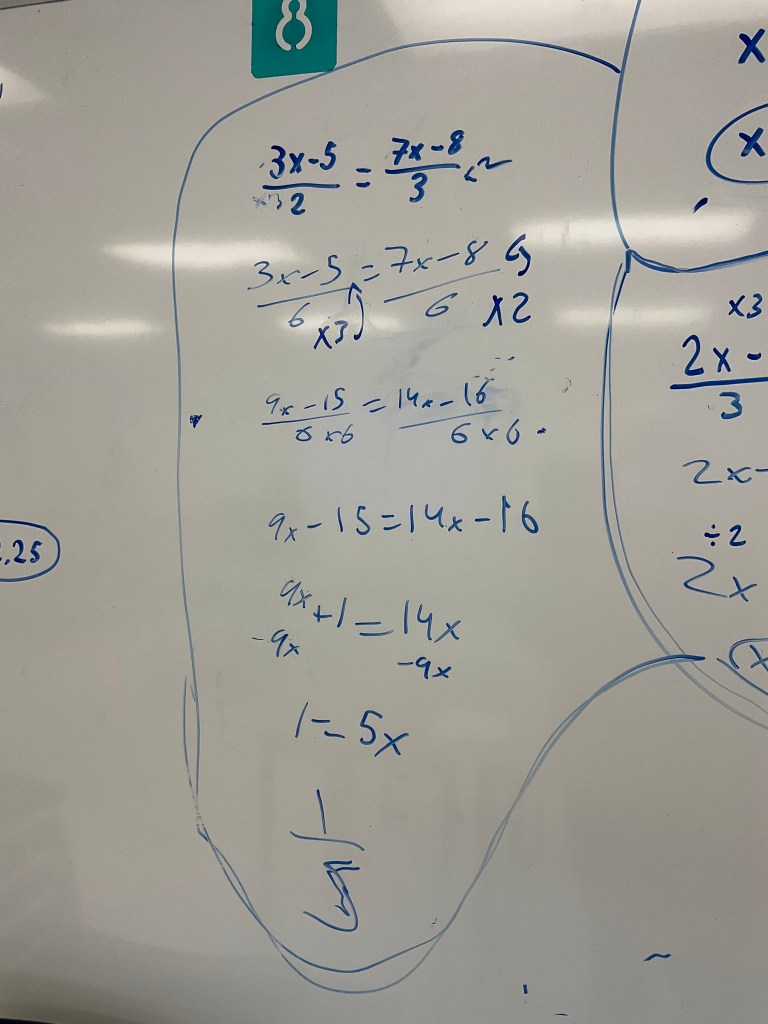
We need to work a bit on our notation, but we’re working through the process of solving in a way that makes sense.
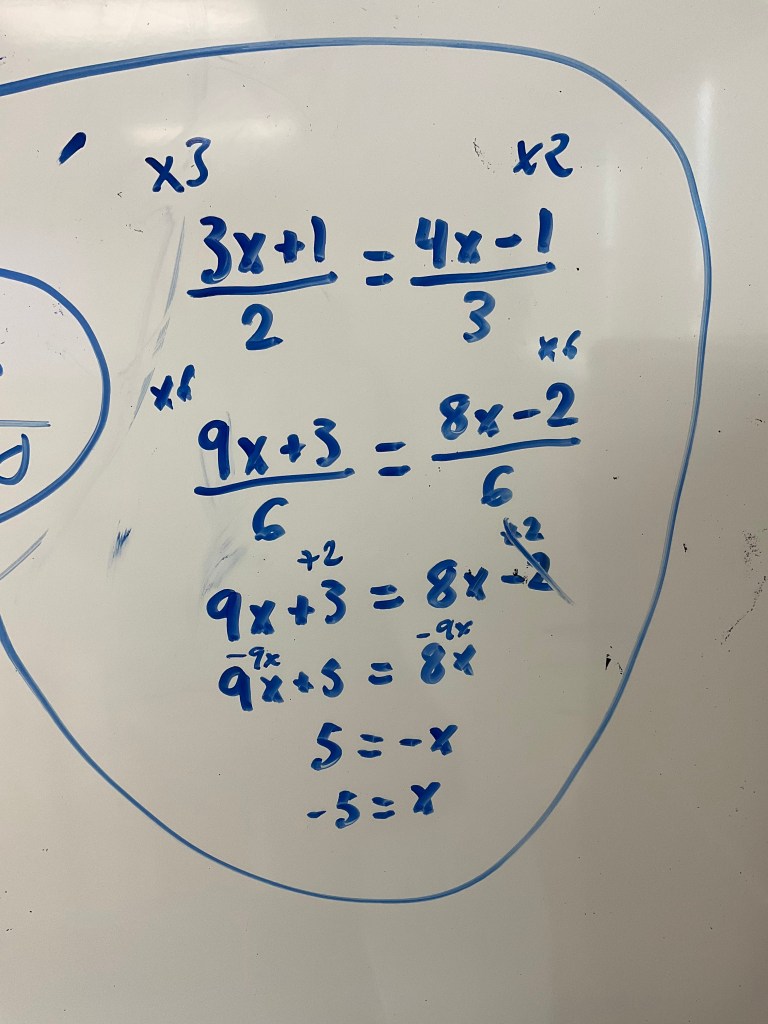
We even figured out how to solve when some terms are in fractions and some are not. We turned the 7x term into a fraction by writing a denominator of 1 before progressing.

It ended up being a very productive class where we bravely solved some pretty complicated equations. I hope we did enough practice to retain the skills until next week.
Introducing Trig Ratios
Today I had the chance to co-teach a lesson introducing trigonometry with a 2P math class. The students started out up at the boards learning how to label right angle triangle sides and angles with lowercase and uppercase letters, and the words hypotenuse, opposite and adjacent sides.
Next they worked through some examples of calculating sides with the pythagorean theorem.

The next challenge was on graph paper: they needed to draw a 90 degree angle on their page. Then draw a right triangle with one angle that is 30 degrees. We estimated the other acute angle, then measured it to be sure. Just to prove to them that angles in a triangle add to 180 we did this demonstration (but I forgot to get pictures).

photo source
Next we used rulers and measured the side lengths of the triangle, as precisely as possible.
We put the values in a table to compare. And I magically was able to judge the accuracy of their triangle skills and accuracy of measuring.
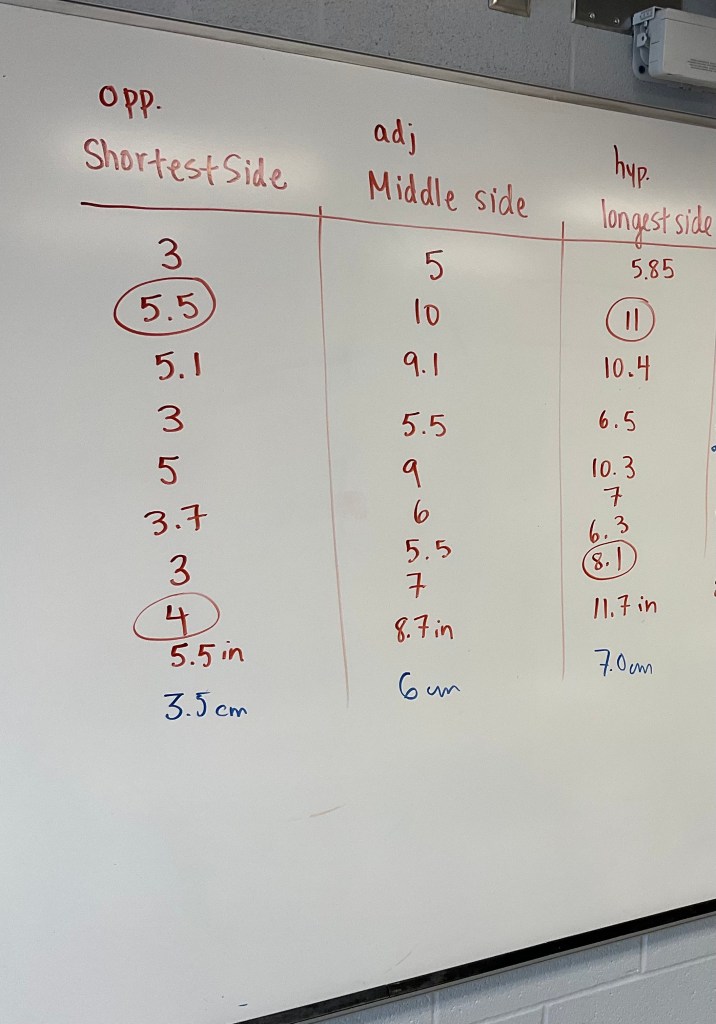
We talked through what was special about the ones that were done “perfectly”. Students identified that the short side was half of the long side for those cases.
From there we explored the primary trig ratios and how to remember them with the acronym SOH CAH TOA.

Citrus Week Consolidation
Today grade 9s consolidated the work for citrus week. The class worked together to place the weight of their fruit on the number line.

We noticed that the smaller fruits had smaller amounts of juice and the bigger fruit had more juice. The orange had the most juice even though it was not the biggest fruit.
The class challenge was to use their information to predict the amount of juice that could be made from 10 oranges.

The class used the information from Gerald the Orange to make predictions. The estimate was that 10 times Gerald would be 3240g which would make 1800mL of juice.
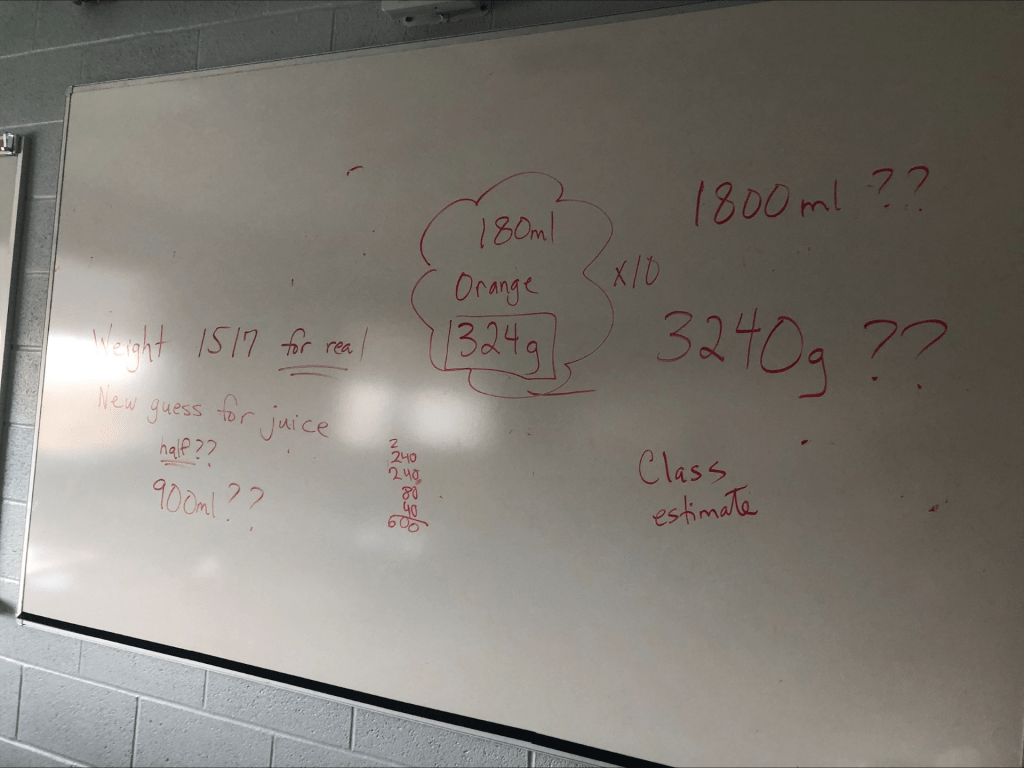
These oranges from today had a weight of 1517 grams which is about half of what the guess was. So maybe the new guess for the juice would be 900mL.
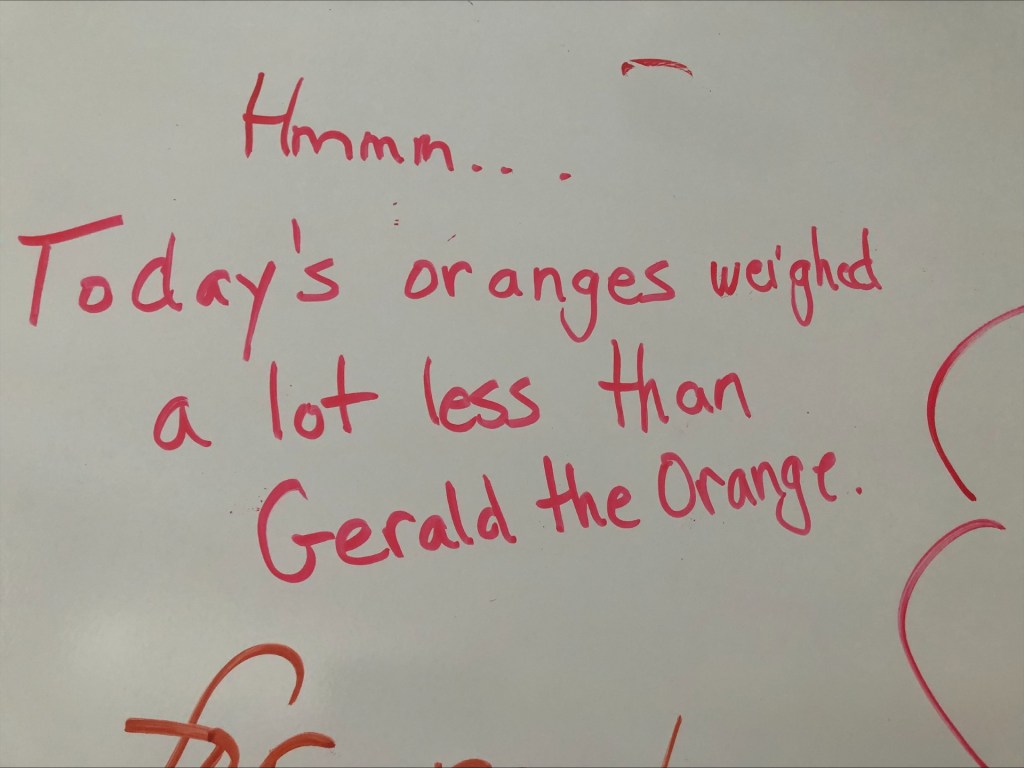
When the oranges were all juiced there was a lot of pulp left in the juicer

There was a lot of juice.

The juice was measured out, and added up. There was a total of 600mL of juice. Less than expected.


There will be more citrus adventures next week!
Citrus Week Day 4
Today we did a lot of juicing. Here’s the juiced lime, which was super sour.

The juiced clementine, which was a much sweeter juice.

and the juiced grapefruit, which made almost 3/4 cups of juice.

Gerold the orange had 80mL plus 80mL plus 50mL of juice which made 210 mL. We had a neat strategy for adding up the mL and showing our thinking.

Citrus Week Day 3
Today we continued to estimate and measure our citrus fruits.
We noticed that the lemon peel can fill 5 lemon sized circles

and the lime peel almost fills 4 lime sized circles.

We measured the peeled lime dimensions

Our clementine had a busy day! It was weighed today.

And we measured the volume as well.

“bumpy” the lemon got juiced today. We found a few seeds.

We tried to drink the juice, it was pretty sour.
Citrus Week (Day 1 and 2)
In MAT1L this week students have been investigating citrus fruits. There are 5 teams, each with a different fruit to explore.
On Day 1 students did a lot of work with estimating and measuring the whole fruit. Groups named their fruit, and drew faces so we know how to orient them when we take measurements.

We estimated and measured dimensions (length, width and height) in inches and cm, we estimated and measured the weight. We estimated and measured the volume in cups and in mL. We used a displacement tank to find out the volume. Here is Gerold the orange having a bath in the displacement tank.

Next we peeled the fruit, and looked at how many circles the peel would fill in. We made circles the same size as the original fruit. It’s pretty cool that the peel will fill 4 circles. The surface area of a sphere is 4(pi)(r^2) which is 4 times the area of a circle with the same radius.
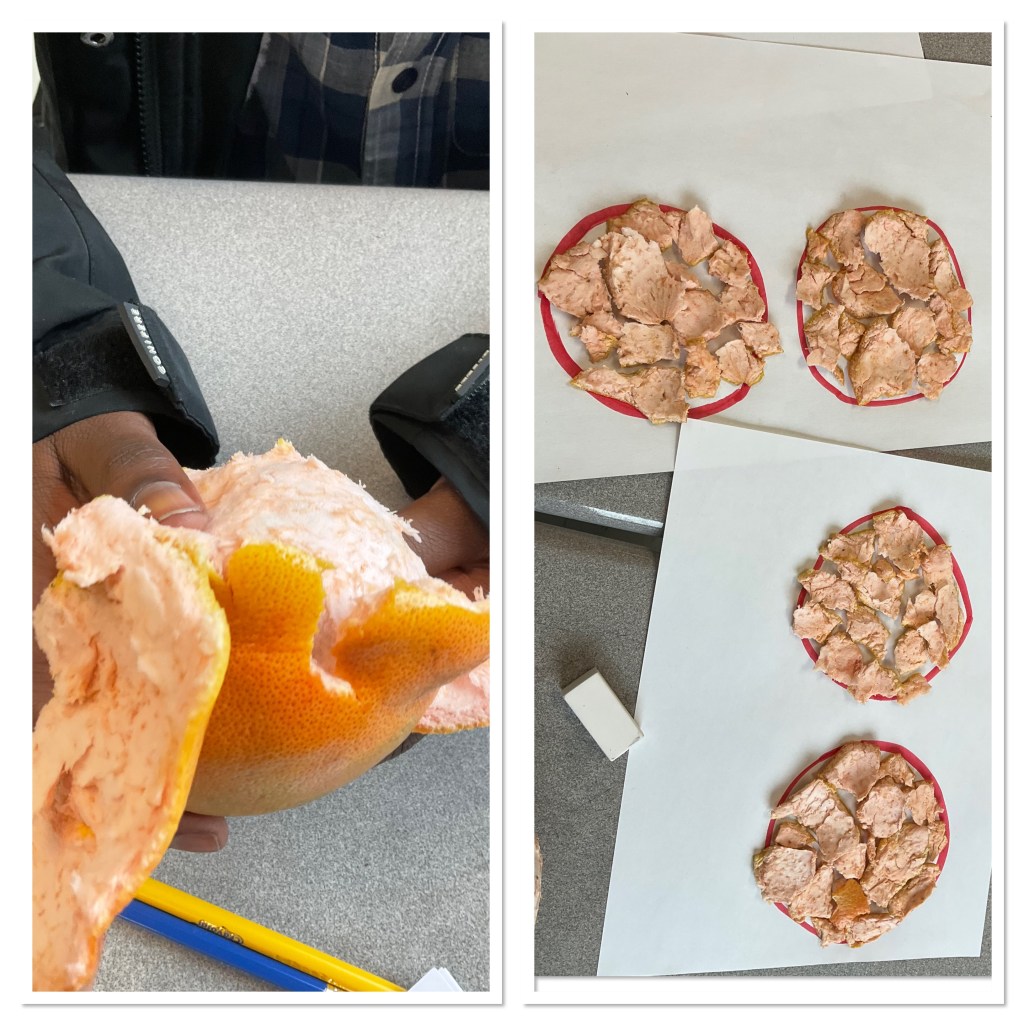
We estimated and measured the thickness of the skin, and the dimensions of the peeled fruit. Then we measured the volume of the peeled fruit.

We will continue exploring as citrus week proceeds! We’ll be looking at the number of segments, and seeds, and then finally juicing the fruit.
Building Pyramids
Today in grade 9 we were looking at the volume of pyramids and cones, compared to their prisms of the same height.
We used water to see that a pyramid can be filled and poured 3 times into a prism, just like the video shows.
We then had the challenge of building square based pyramids with a volume of 300 cubic centimetres.
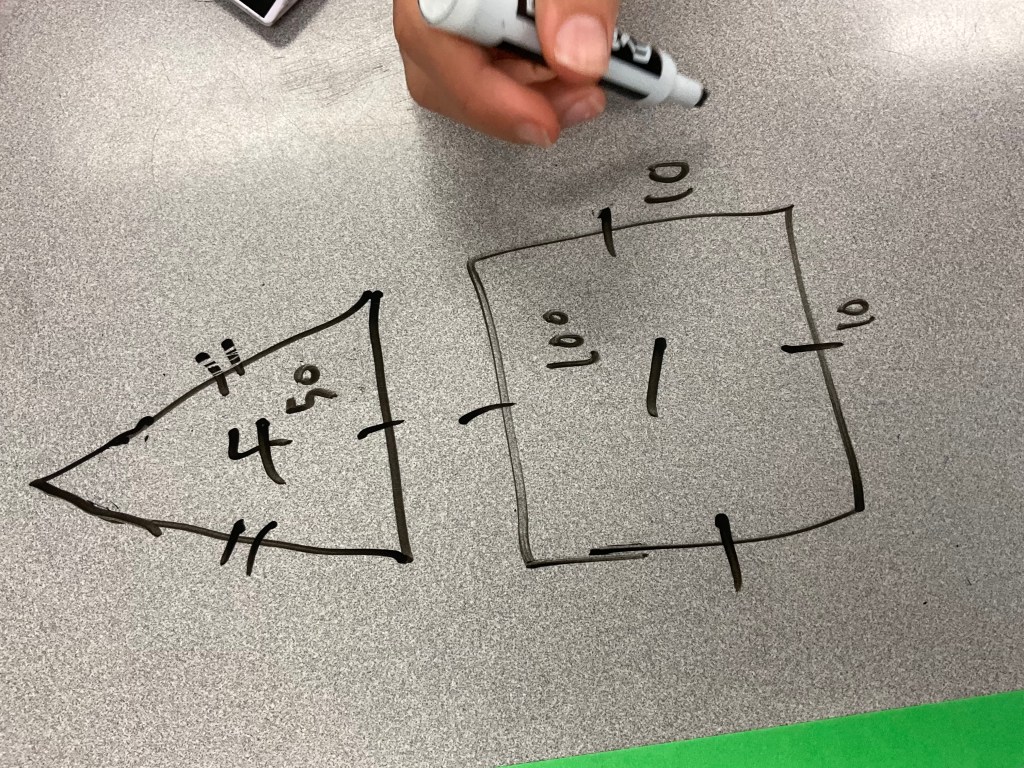
We know that the volume of the prism with same length, width and height as the pyramid would be 900 cubic centimetres.

We noticed that many groups made pyramids that were shorter than they had planned.

Many groups had not considered that the slant height is different from the pyramid height, and we need to use the pythagorean theorem.

There was a good amount of productive struggle in each group as we needed to readjust our triangles a few times to achieve the correct height for the pyramids.
Surface Area and Volume of Rectangular Prisms
Today in grade 9 we built rectangular prisms with a volume of 300 cubic centimetres. There was a lot of freedom of choice. Students could choose the dimensions that they wanted to, as long as the volume worked out.

They then used cardboard to create their prism.

Some groups had interesting strategies for coming up with their dimensions. One used the box that they had, because it was already a rectangular prism, and they just needed to determine the height, and cut it to size.

It was 19.5cm by 16cm, which already is bigger than 300 when multiplied.

there was some excellent trial and error involved in calculating the height of the prism, and that it needed to be between 0 and 1.
Groups worked on building their prisms, and then calculating the surface area when they were finished. Some groups who were up for a little extra push got the challenge of building a cube, or building a second prism with a larger or smaller surface area.

This was our time to review what prisms are, and how to use the formulas to calculate volume and surface area, and also to introduce the idea that an object with a specific volume can have a different surface area depending on the dimensions.

Students have already done these calculations in elementary school, but they may not have seen that there is such a variety of possible prisms for the same volume, nor how different the surface area can be.
We took all the finished prisms and put them in order by surface area.

Cubes have the smallest surface area, and the more worm-like, or plate-like prisms had the largest surface areas.
We connected the idea of surface area and volume to packaging problems, where you could spend less money on packaging if you use a cube as a box. We also talked about how cells divide when they get too large, to maintain the optimal surface area to volume ratio, how worms can breathe through their skin because they have a big surface area compared to their volume, and how we have a large surface area in our lungs for gas exchange.
We also talked about how you can find the dimensions of the cube with volume 300 cubic centimetres, by using the cube root on a calculator.
We will build on our prism knowledge and next week tackle the fun challenge of building a square based pyramid with the same volume.