Introduction to Loom Beading
We are happy to have the Indigenous Program team with us this week as we do loom beading with 2 of our grade 9 classes. Today we started with an introduction to loom beading, and the sharing of teachings. We learned to keep a good mind while working, and to put positive intentions into our work.

We talked about the different math that can be explored through beading. Concepts like symmetry, rotations, reflections, area model, percent that is a certain colour, lines, parallel lines, slopes, intersections, shapes, angles, proportional reasoning about how many red beads to add for each pattern repeat of 3 rows etc…the list goes on!
Students then designed their patterns, and started beading.

We learned the process for getting started. Thread 11 beads onto the needle. Bring them under the work. Pop them up through the strings with one bead between each pair of strings, and then thread the needle back through, on top of the strings this time.

it was impressive to see the progress students made in one period!

Thanks to our guests who shared their knowledge, experience, and teachings with us today.
Speed Dating Review
We’re working on reviewing material for our upcoming test next week. Today we looked at algebra: simplifying with exponent laws and also expanding and simplifying polynomials with distributive property, and collecting like terms.

Partners sat across from each other and solved the question together. Then one side of the partnership stayed as the expert, and the other side stood up and moved one space to their right. They then attempted the new question with help from the expert that remained.

They then stayed as the expert and the other side of the table moved to their right. Students have the opportunity to work in multiple partnerships, and they work through each question twice, once as a beginner and then again as an expert.
It’s a pretty fun way to do review!
Thin Slicing: Solve By Factoring
Grade 10s are working on applying their factoring skills. We have looked at how we can graph parabolas from factored form, and now we are looking at how to solve quadratic equations by factoring. This is the sequence I used to develop the skills today.
(x)(6)=0 and (8)(x)=0

Then we included coefficients. Some groups really clicked into the idea that if the product is 0 one of the factors must be 0.

The next question was interesting, as there were 3 representations of solutions.
(11)(x+1)=0
One group did the area model to expand, another used the distributive property without the area model to expand then solve, and there was one group who knew that (x+1) would need to be 0 and solved quickly.
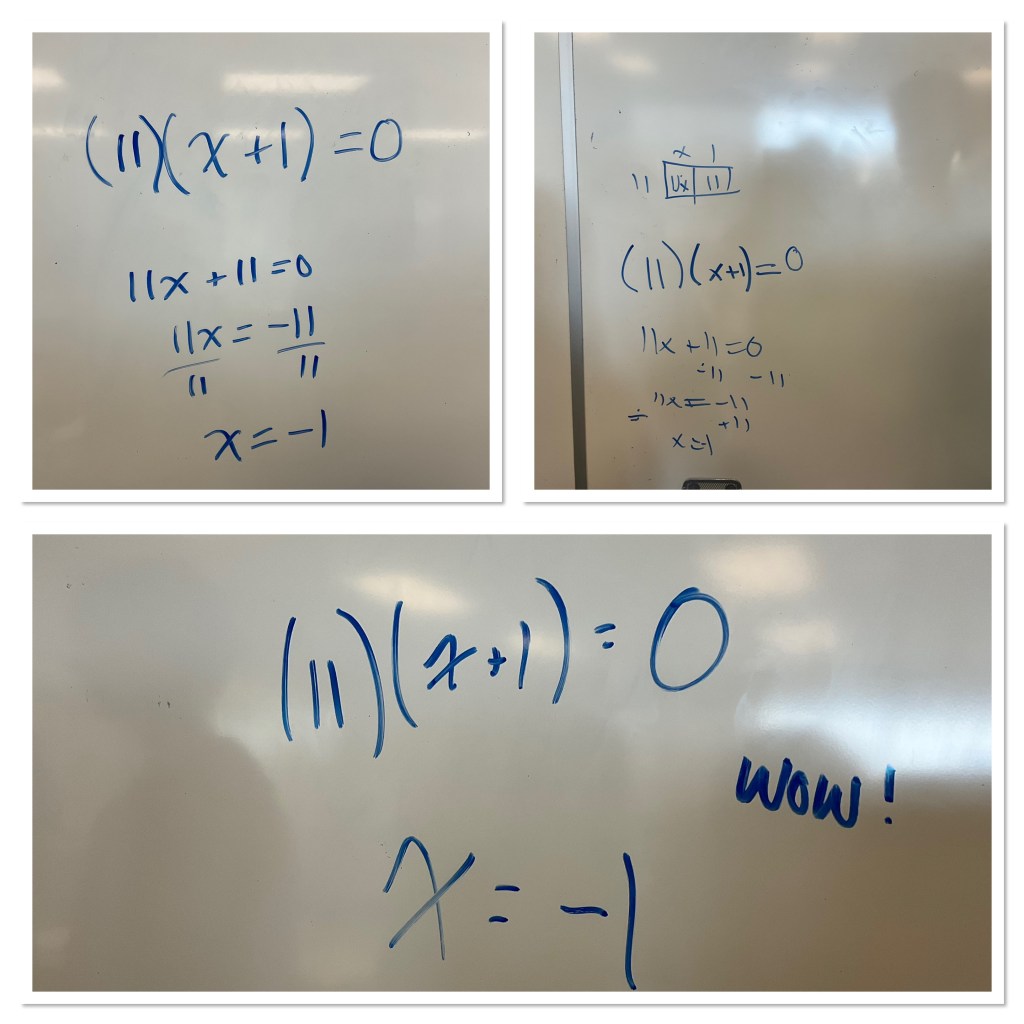
We practiced a few more examples and many groups latched onto the idea of solving without expanding.

The next introduced a coefficient, and it was interesting to see how students approached it. Some realized that we multiply 2 by 2.5 to get 5 which is the zero pair of -5 which is in the bracket. Others approached it as if it was x-5 in the bracket the x would be 5. Since it’s 2x in the bracket then the x must be 2.5.
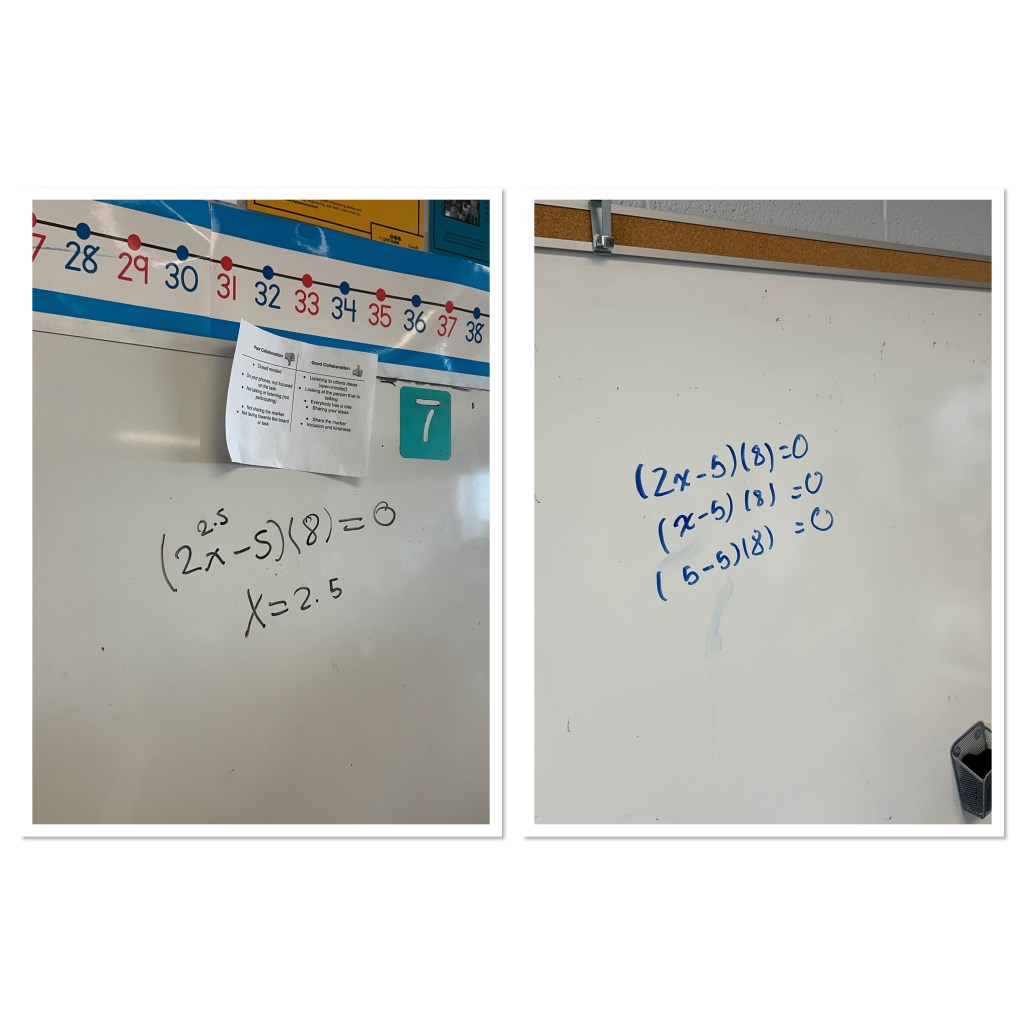
Our next step happened after students were comfortable solving by setting brackets equal to 0. We tried (x-1)(x+2)=0

It was neat to see how they were ok with their being 2 answers. We made the connection to a parabola passing through the x axis twice, so it’s ok to have 2 answers.
I wanted to avoid students always thinking that the constant in the brackets is connected to the answer, so I introduced coefficients quite quickly to enforce the idea that we need to fin the x which makes the bracket equal to 0.
Next we looked at what happens if we are not given factored form, but instead a trinomial equal to 0. We need to factor first and from there it’s all the same as before. We use the area model for factoring because it connects so well to algebra tiles and how we expand polynomials too.

The next step sequentially was to start with an equation without 0 on one side. Students knew to use zero pairs to create an equation equal to 0 and then to factor and solve.

The sequence worked really well, and I hope that students will continue to be able to apply their skills to solve quadratic word problems next!
3 act Task: Taco Cart
Grade 9s have been working on learning the pythagorean theorem. We’ve had a look at this video:
We know that the sum of the squares of the perpendicular sides of the right triangle is equal to the square of the hypotenuse. We then used that knowledge to help us with the 3 act task:
For 3 act tasks, students are working at the walls in random groups of 3 with one marker between them. They start by making a “notice and wonder” table where they list the things they notice and wonder while watching the act 1 video clip.
Next students try to determine who gets to the taco cart first. To do so they need more information which is withheld until they ask for it. Students will need the dimensions of the pathways, and also the speed that they walk in the sand and on the road.
Here are the images to help fill in the details, and for Act 2 the students work together to solve the problem.


Students worked together to solve and show their work
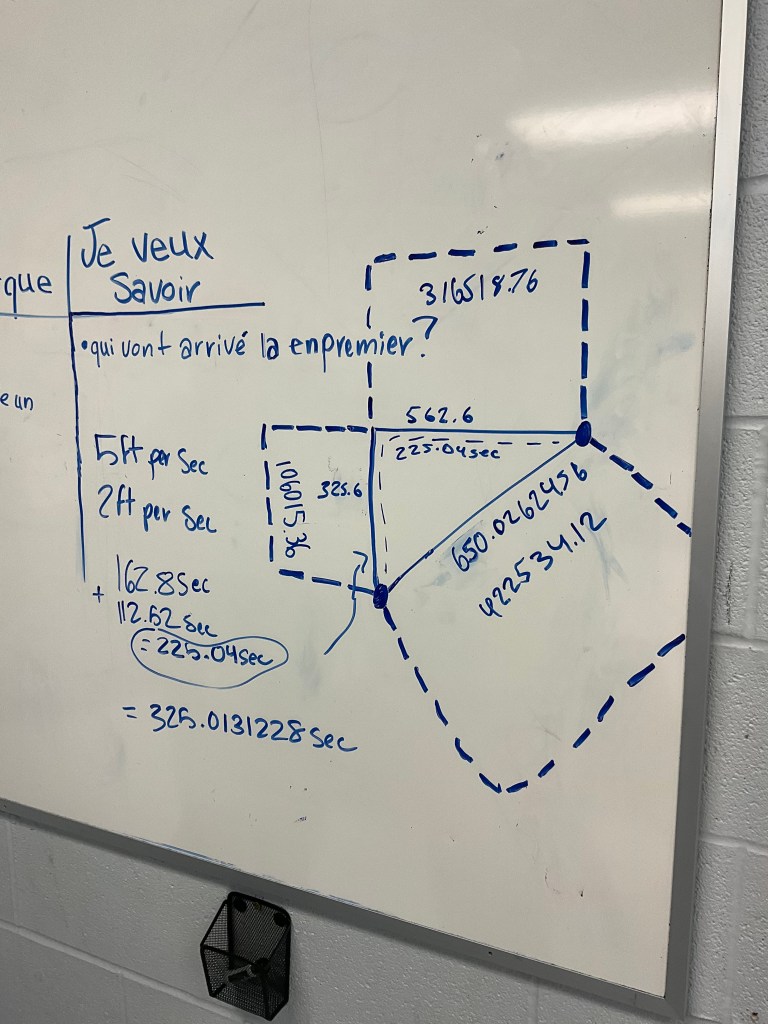
Extensions I asked were: what’s the time that it takes in minutes? How far ahead was one compared to the other?
For Act 3 we had a look at the features of the various student solutions. The use of a clear diagram, and showing calculations and explaining a bit about how to think through the rates of ft/s and how that affects the answers, and then how to convert to minutes. We then watched the 3rd video and saw how close we came.
Students are getting really good at working together. We have been practicing all term and it is great to see progress and increased confidence.
Fractions, Decimals, Percents
Grade 9s are going to be working with fractions and decimals and percents coming up. Today we worked on putting them in order, as a diagnostic collaborative activity. I’m uncertain which gaps exist in this class due to what work would have been missed during COVID lockdowns years ago. There have been different gaps this year that I have noticed, with perimeter, and I wondered if fractions may have also fallen through the cracks more than in the past.
Students worked in their randomly selected table groups. Groups were given a handful of assorted cards. White cards are fractions, green are percents and yellow are decimals. They needed to work together and use their strategies to sort the cards from smallest to biggest.
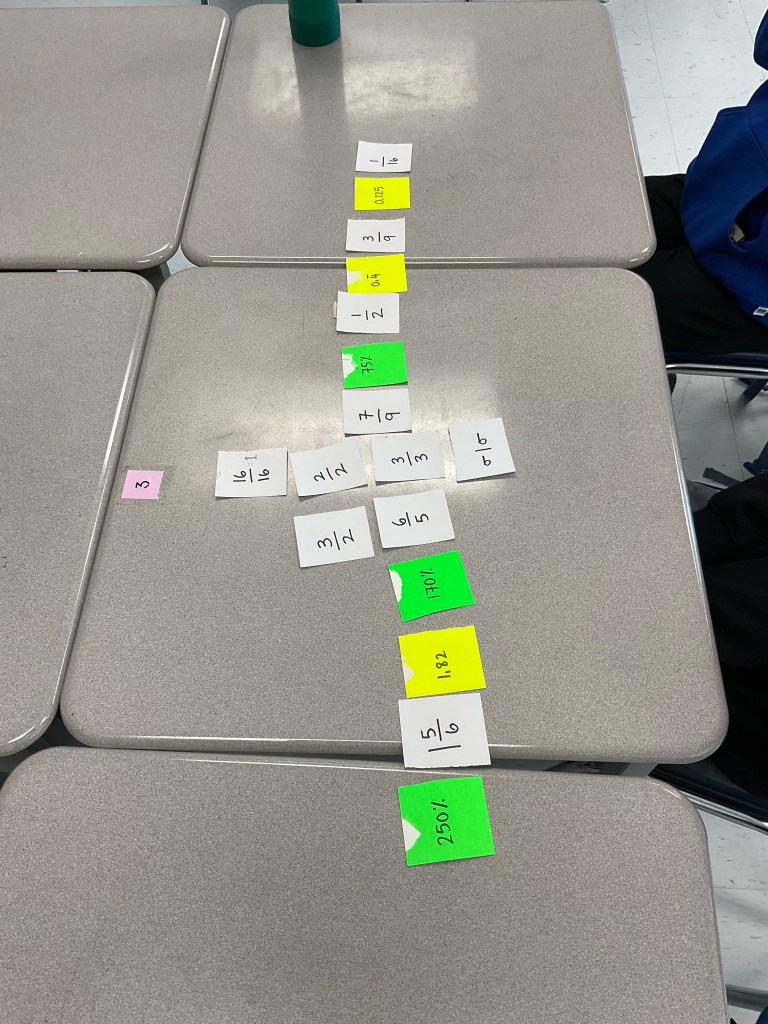
Groups chatted about how to tell if fractions were big or small (if they were in mixed numbers they looked for the whole numbers, they also looked for improper fractions where the numerator is bigger than the denominator). They were very confident ordering decimals, and ordering percents, but putting decimals and percents together took some thinking.

Each group then sent a volunteer with their smallest value to chat and decide what the smallest smallest value is, and we started a communal number line. They sent a different volunteer with their largest values to chat about which one was the largest largest value and put the other end point of our number line on the board. Next everyone placed their cards in order, and made sure the number line made sense.

We talked a bit about what fractions mean, and how to represent them, and we chatted a little about what numerators and denominators are. We learned that if we divide numerator by denominator we can make a decimal, so we can convert fractions to decimals and compare the numbers nearby. We also noticed that decimals and percents differ by a factor of 100, so to convert decimals to percent we multiply by 100% and to change percent to a decimal we divide by 100%.
We talked about comparing fractions as well. If the fractions have the same denominators we know that the unit rectangle is split into an equal number of pieces (the denominator) but we are discussing different quantities of pieces. E.g, 3/5 compared with 2/5 we know that the unit rectangle is split into 5 pieces. One fraction talks about 3 of the 5 pieces, and the other fraction talks about 2 of the 5 pieces. I know 3/5 is bigger than 2/5.
If the numerators are the same and the denominators are different we can compare them easily as well. E.g. 3/8 compared to 3/9. I can imagine a rectangle split into 8 pieces and a rectangle of the same size split into 9 pieces. If it’s split into more pieces the pieces are smaller. If I have 3 larger pieces compared to 3 smaller pieces, I can conclude that 3/8 is larger than 3/9.
We then worked on correcting the order in the number line.

The final challenge was to space our numberline properly. We set benchmark values of “friendly numbers” like 0, 0.5, 1, 1.5, 2, 2.5 and then each table group sorted and spaced one of those sections of the number line.

We have some work to do, but during this activity students were able to explore and try and reactivate ideas from years ago. Some expressed that they were very unsure of fractions in general. We will work on these topics for a while, then try a similar task later and see if they feel better about the strategies we have learned.
I captured photos of their finished numberline. We may look back at these photos next week and see if we can find things to correct, or discuss.





Math Outside!
It has been such lovely weather that we decided to do math outside today! My grade 10s joined with the grade 9s from across the hall, in intermixed groups and we represented algebra with toothpicks.

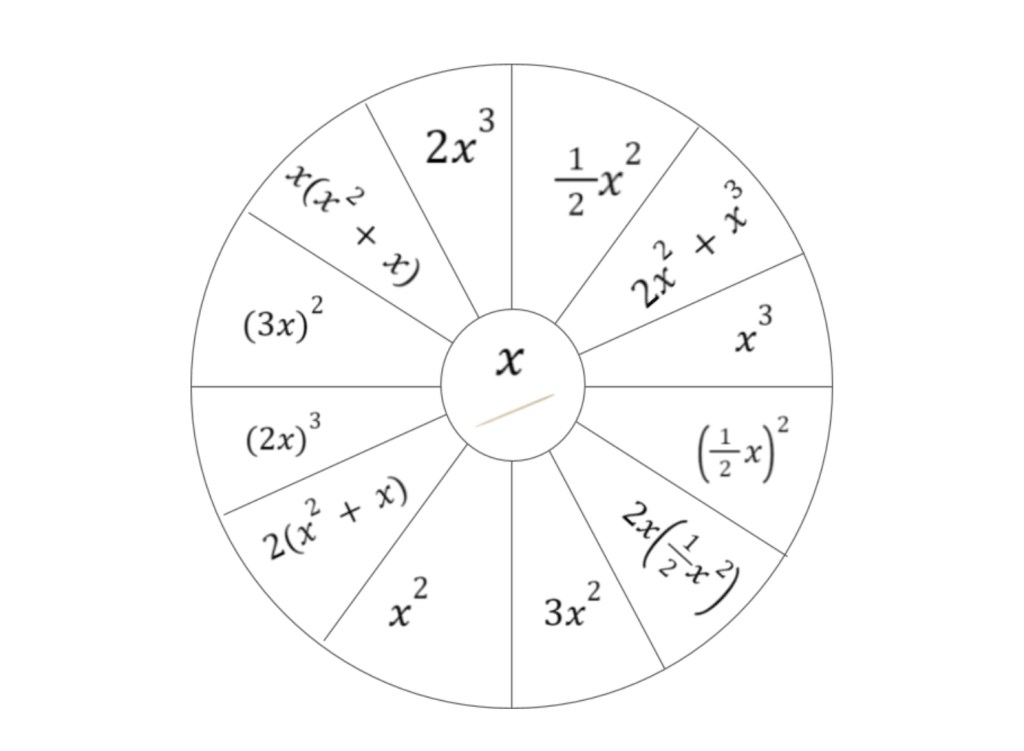
We provided each group with a page that had written expressions, then groups built physical representations and showed them on a concept circle.

It was great to see the grade 9s and 10s work together to build their models. Students were problem solving and challenging each other’s misconceptions. We had a lot of interesting discussions about what brackets mean, and what (2x)(1/2x^2) would mean. Would it be just the same as building an x cube, since if you multiply it that’s what it gives you, or if you need to build a rectangular prism with the base area as (1/2x^2) and the height of (2x) (as seen above).

Since we were working outside we had loads of space, so we made our concept circles bigger, but also contain more slices. Here is the total circle.
We had a spicier one ready to go, but didn’t need it.
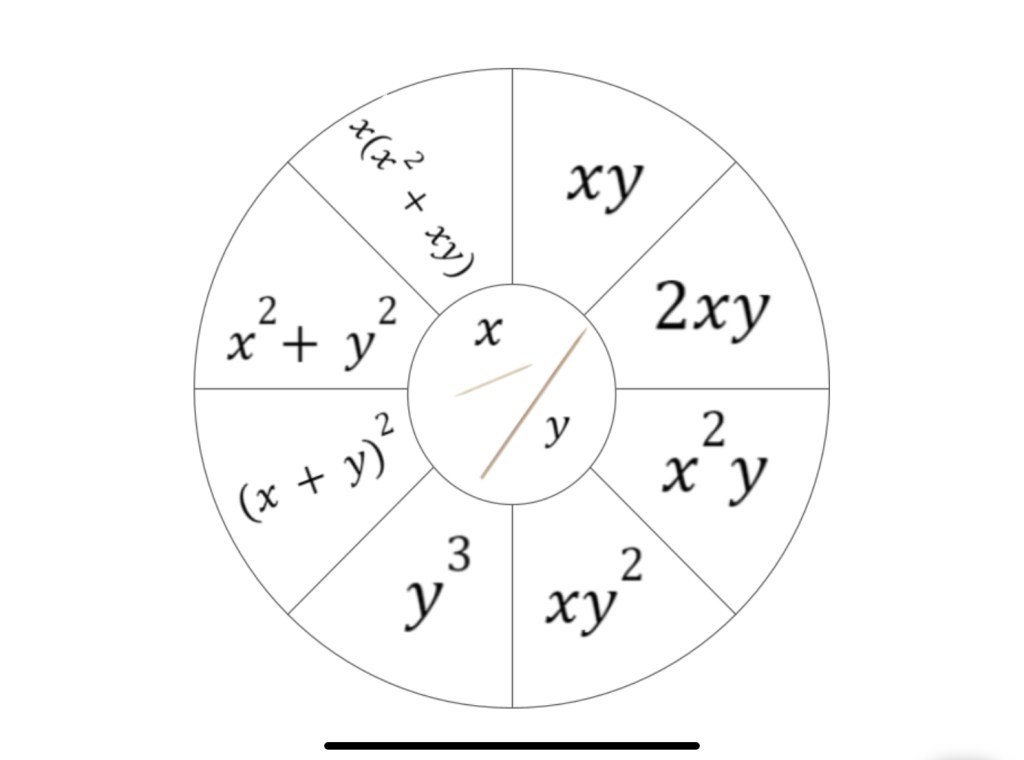
We also had ideas of asking as an extension to build an (x+y)^3 which I think would be fun to see.
Thanks for the great fun and collaborative work today students!
Exponent Laws Continued
Today grade 9s finished working on exponent laws. We looked at power of a power today. We noticed that you could write out (5x^3y)^2 as (5x^3y)(5x^3y) and then use the multiplication law to get to the answer.

After a few questions it got a bit boring to write things out long form, and we noticed some patterns. We need to apply the outside exponent to the coefficient in the brackets. We also can multiply the outside power with the inside power to get to the answer.

We got really good at this and then upped the spice level to try some questions with power of a power AND multiplication as well. This picture was taken partway through the problem. The final answer is 432x^10y^6.

We’re practicing how to simplify using a mixture of the laws now.
Exponent Laws Continued
Grade 9s were hard at work today continuing on their exponent laws journey.
We explored some examples with numbers.

We learned that if we have a fraction with the same numerator and denominator it simplifies to 1. Each of the circled pairs will simplify to 1. We can now express the answer as an exponent. When we divide and the bases are the same, we can subtract the exponents.
This works if the base is a variable as well.
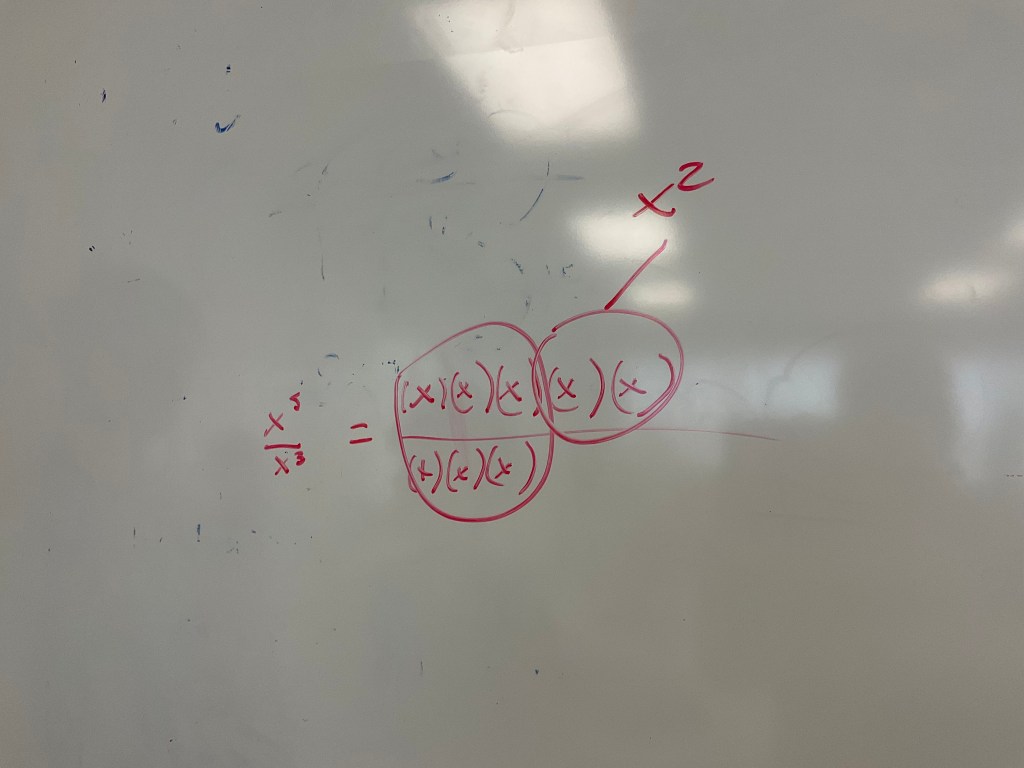
The next example includes coefficients and 2 variables. We know that we divide the coefficients as normal. 12/6=2. We look at the xs next. We have x^(4-2) which is x^2, and something neat happens with the ys. We see that when we subtract the exponents we get 0. We also see that we can circle the y^3 in the numerator and denominator and that this fraction will equal 1. Anything to the power of 0 will be equal to 1.

The next example leads us to explore negative exponents. We can easily manage the fraction and the as, but when we have b^(4-6) that leaves us with b^(-2).

We explored how to write negative exponents another way. When we have a negative exponent, it has come from a case where the exponent in the denominator is higher than the exponent in the numerator. If we write it in developed form and circle all the fractions that equal 1, then we will be left with variables in the denominator. a^(-2)=1/(a^2)

We consolidated our work, and made a note in quadrants. Students made their own examples, and we co-created a list of things to remember and write down.


I sent a mass email to students and families with this homework task: Students should explain how to do this question tonight or over the weekend.

Exponent Laws Introduction
Today grade 9s were working hard to represent multiplication in many ways. Here’s a sequence of questions that led us to the exponent law for multiplying.
Represent 4 times 2 times 3:
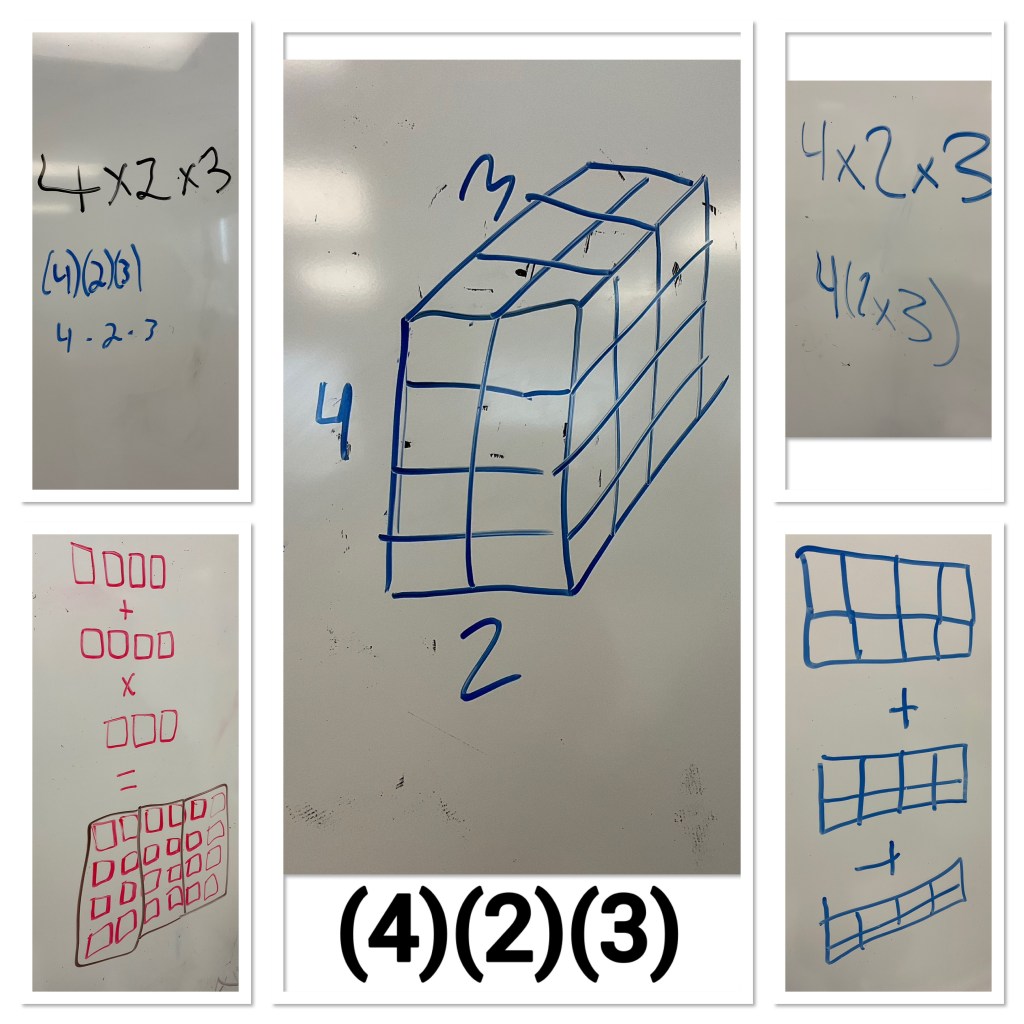
Students showed in many ways that they understood what (4)(2)(3) is.
Represent 3 squared.
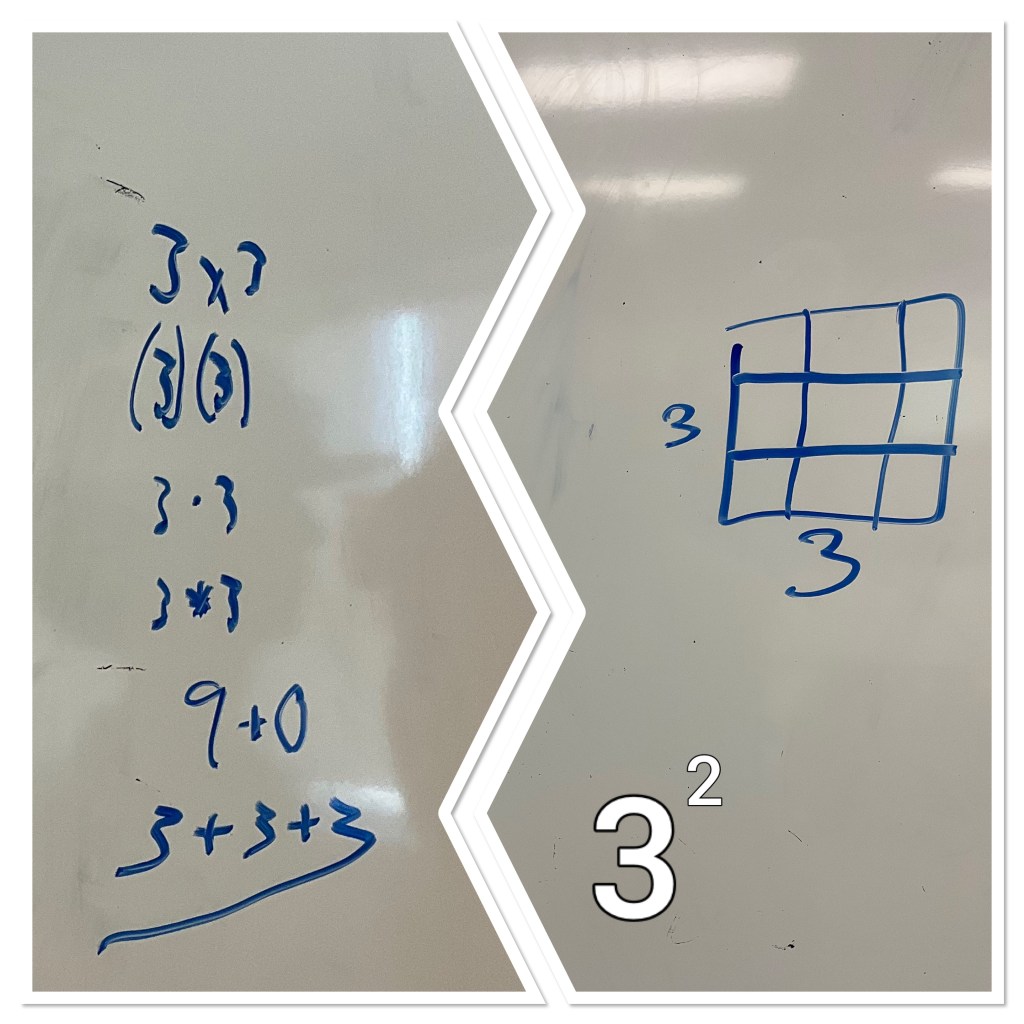
Following what we did yesterday, we know that the exponent 2 means to make a square. The side lengths are 3. We know we can write (3)(3) in many ways as well.
Represent 4 cubed:

It will take 64 little cubes to build a 4x4x4 cube.
Represent x squared.
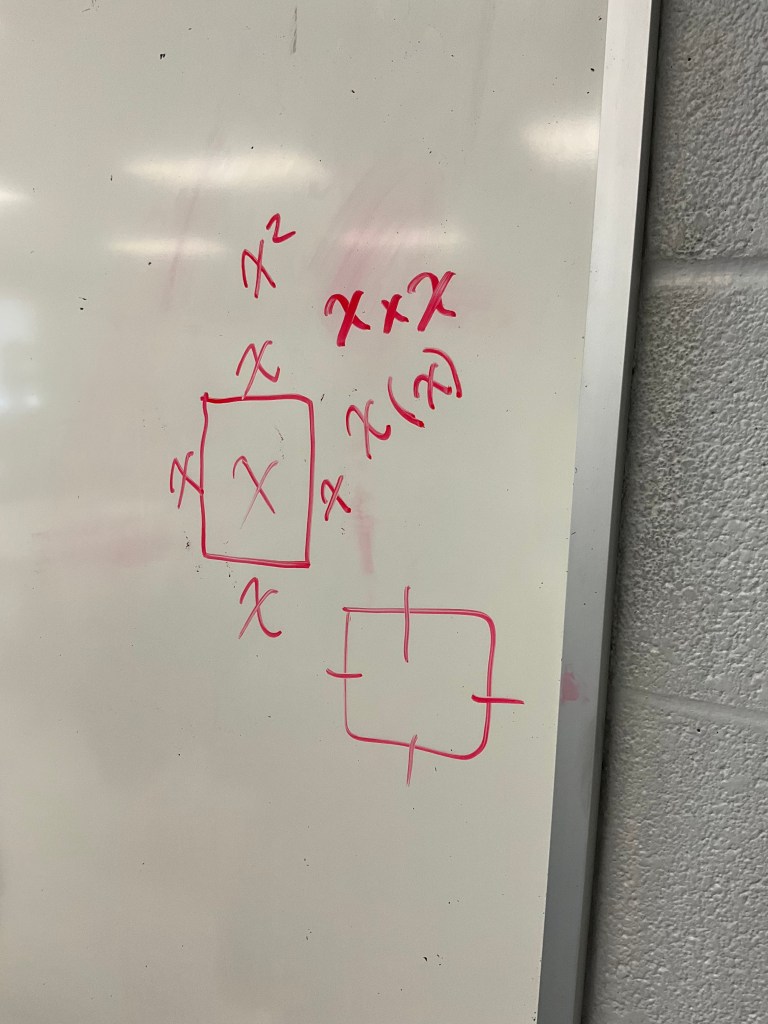
Represent 2x^3

2(x)(x)(x) is another way to show it.
Represent 2x^3y^4

Represent 1/2x^4z^2p^3

We noticed that there is a hidden multiplication between all the letters.
Represent (x^4)(x^2)(x^3)

We can see so many (x) multiplied together, and we can represent this as x^9. When we multiply and the bases are the same we can add the exponents.
This next question was more challenging because we now have coefficients involved.
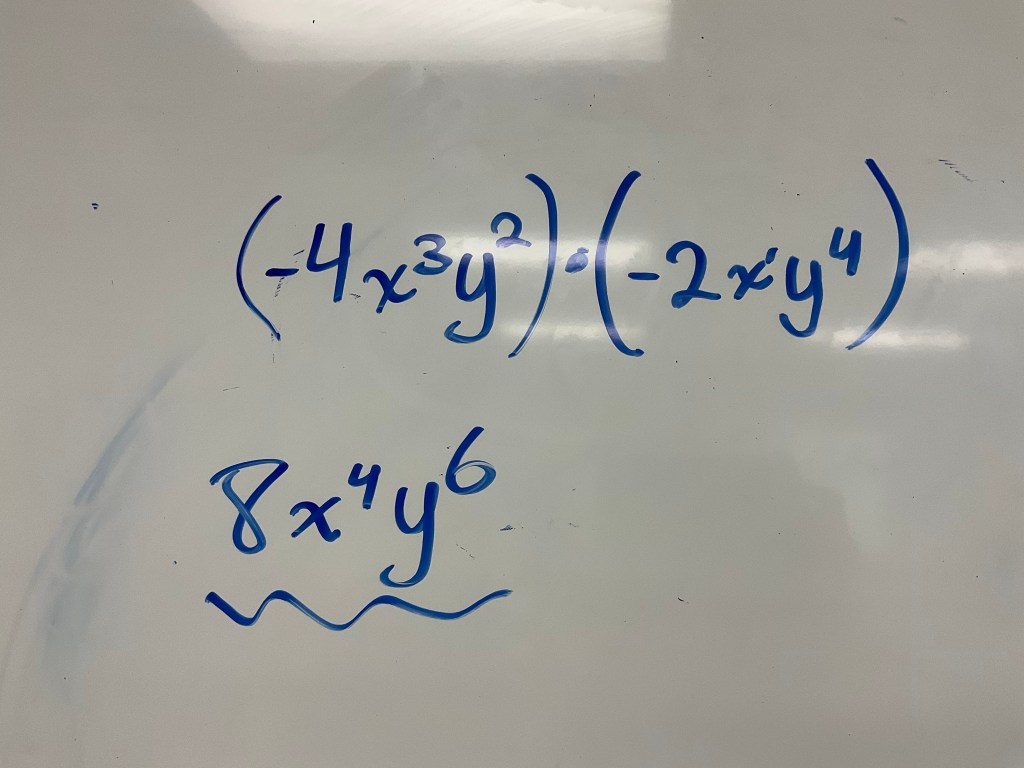
(-4)(x)(x)(x)(y)(y)(-2)(x)(y)(y)(y)(y)
this can be written as (-4)(-2)(x)(x)(x)(x)(y)(y)(y)(y)(y)(y) since the order doesn’t matter when we multiply.
It was a busy fun class today! Well done grade 9s.
Representing Exponents
Today my grade 9 class built exponent models using toothpicks and plasticine. The mild version included x^2, x^3, 2x^2, 2x^3, (2x)^2, (2x)^3, 1/2x^2 and (1/2)^2.
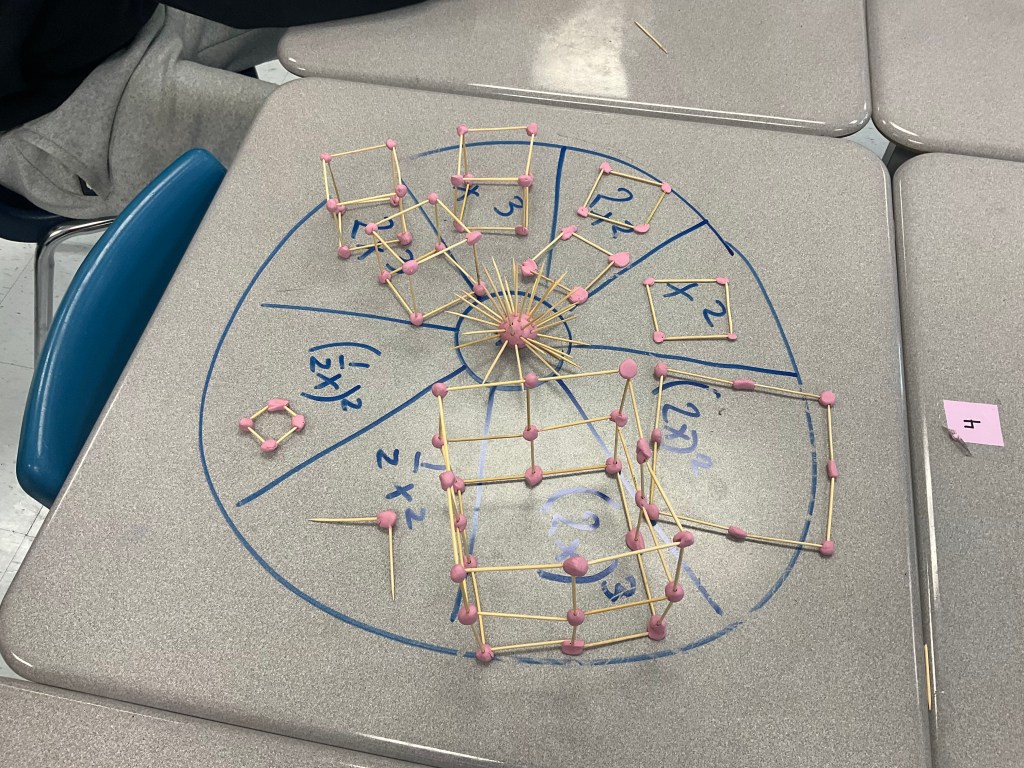
The x is a toothpick, so x^2 is a square (x by x). We made connections between the exponent being a 2 meaning we build a square, and if the exponent is 3 we build a cube. The base of the exponent represents the side length of the cube or square, and the coefficient will tell you how many to build.

We had a very carefully prepared (2x)^3. We can clearly see that it is made up of 8 little x cubes. This helps us see that if we double the side length of a cube, the volume will be multiplied by 8 (2^3=8). In the same photo you can see a (2x)^2 which helps us see that there are 4 x squares in it. When the side length of a square is doubled, the area is multiplied by a factor of 4 (2^2=4).
We moved on to a spicy concept circle, including skewers for y and toothpicks for x.

We had some interesting conversations about where to start. Some groups gravitated to the (x+y)^2 since they knew they were making a square with side lengths of (x+y).

We were able to split up the (x+y)^2 into x^2+y^2+2xy. We also showed that (x+y)^2 is NOT equal to x^2+y^2.

Other groups got into building the rectangular prisms with dimensions (x)(y)(y) or (x)(x)(y)

We noticed that an x^2y and an xy^2 were not the same. We could identify which was which based on the square that we saw. This one in the picture is an xy^2 since we see the skewers making a square.
I think we had many lightbulb moments today as we explored what exponents mean. We will continue exploring exponents for the next few days as we look at exponent laws.