Ms. Bearse's Site

We’re working on calculating perimeter and area in our 1L math class now.

Today we modelled a rectangle on the floor, and made use of the tiles to help us determine the perimeter and area.

We know that to determine the perimeter, we add up all the sides, or we can add the length and width and then double the result, or we can double the side lengths and then add the results.

To determine the area we we are working on multiplying. We know we can count the squares, or we can multiply length by width by skip counting, or by making groups.

We followed up with another area game!

We’ve got last minute test preparations happening today. We worked in pairs at the boards, and solved questions at stations around the room.

We are now able to do many skills. We can calculate the surface area and volume of spheres, cones and square based pyramids, we can optimize the surface area and volume of rectangular prisms, we can calculate the perimeter and area of composite shapes, and we can represent exponents in 3D models (using toothpicks and skewers and clay).

We’re ready for tomorrow’s test!

We played a game in 1L today to help us practice the area of rectangles.We played in pairs. Each person took a turn to roll 2 dice, and then colour in a rectangle with the dimensions of the numbers on the dice. Each person needed to then state the area of their rectangle. There was some strategy about where to place the rectangles, to mess up the future plans of your opponent.

In the end, to determine who won, we needed to determine who had the most area coloured in. We divided up the regions into smaller rectangles and calculated those areas and added them up.

Grade 9s are working on problem solving and using a formula sheet. We’re clearing up confusion before our test on Thursday.

We are working in pairs, and helping each other. We need to read questions well to be sure we know what we should be finding, and how to go about it.

We learned some new words today in 1L. We know that the circumference is all the way around the circle. We know the diameter goes across the middle of the circle from one edge to the other, and the radius goes from the center to the outside.

We traced many round containers and objects, and measured the diameters and circumferences.

A good strategy for measuring around an object is to use a measuring tape, or a piece of string.

We put all of our information into a chart, and then made a graph from our data. We noticed that our graph had all of the points in a straight line. We can use the trends that we see to help us estimate the circumference of a circle if we know the radius.

In 1L we’re working on making rectangles with a perimeter of 24. That means that if we count up the edges, we get 24 as an answer.

There are a few different ways to make a rectangle with a perimeter of 24. Here’s a rectangle that is 1 by 11. If we add up 1+11+1+11 it makes 24.

we saw some patterns when we organized all of our rectangles by size. When the length increases the width decreases. We also noticed that length plus width is always 12 in this case. Which is half of the perimeter.

So another way to calculate perimeter is to add length and width and then double the answer.

Grade 9s are working on understanding how to calculate surface are and volume these days. Today’s activity shows how to calculate the surface area of a sphere.

We measured an orange, and drew 5 or 6 circles with the same diameter.

We then peeled the orange and filled the circles, like a jigsaw puzzle.

We can always fill 4 circles with the peels. We know already how to calculate the surface area of a circle, A=(pi)(r)^2, so the surface area of a sphere is A=4(pi)(r)^2.

In 1L today we practiced counting coins, and making change for purchases.

Grade 9s are working hard to represent expressions with exponents using toothpicks and skewers. We call the toothpicks x and the skewers y. We can build shapes with volumes like (x)(y)^2 and (y)(x)^2 now and we know how they are different. We can represent the surface areas also, since we know that each side is a rectangle, and the area of each rectangle is length times width.

We are working on our understanding of how the parentheses will affect the finished model. The important thing is to understand what the exponent touches will be the dimensions of the object.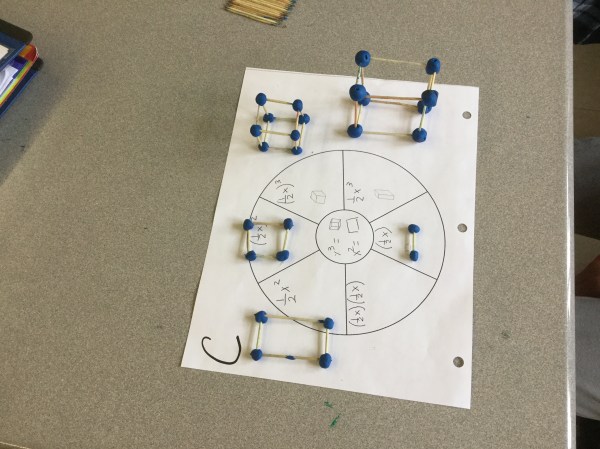We’re getting the hang of it!

In 1L we worked on fractions, and learned how there can be many representations for the same thing. We can have a visual, a numeric, and also a worded description.

We built fraction models using cards at the board. Here is an example of 4/9 or four ninths. We have nine cards total, and 4 are pink.

Fractions bingo is a game where a fraction gets called out, and then we get to decide which representation to colour in. The goal is to fill in a complete line.