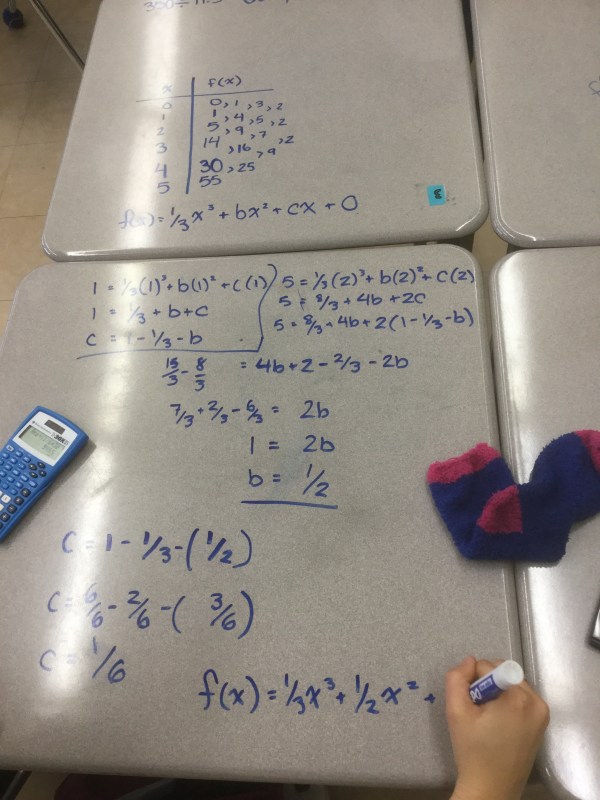Ms. Bearse's Site

Once again we were displaced due to a math contest, but we can still do lots of good quality math in the library!

We are getting much better at simplifying what look like very complex expressions.

we have been doing a lot of work on factoring and expanding….connecting trinomials to their binomial factors is a good challenge! Here we have sticks with a trinomial on one end and some factors on the other end.

Our goal is to connect all the equivalent expressions. Some went about multiplying the factors, and others factored the trinomials…

This activity has a few “tricky” (very similar) expressions, and an extra trick that one stick does not belong! This is easy for teachers to know who has just joined up all the sticks to be “done” first….or who has actually finished the activity because 9 sticks form a ring, with one left out.

Today we took a look at some EQAO questions that deal with algebra, expressions, and simplifying.

We worked up at the boards, and moved around, solving questions at each station, then checking our answers, and erasing so the next group could try.

Some of our questions were hard to do on a calculator because the numbers were so big. We used exponent laws and that helped us manage.

Our beans are starting to grow tall enough to measure them. We are tracking their growth and will make a graph comparing the growth rate of our beans.

Good luck grade 10s and 12s!

Grade 9s are working on simplifying algebraic expressions, and adding and subtracting expressions. We are using algebra tiles to help us visualize the abstract algebra concepts.

We can represent the addition of these polynomials using tiles. Red tiles are positive, blue are negative. Big squares are x squared, rectangle tiles are x, and small square tiles are 1

When we add these together some tiles will cancel out. We end up with a trinomial -x^2+5x-2

Some of us are working hard to maintain our growth mindset and dive in to analyse our recent errors on tests.  It’s not a comfortable activity to spend time with our errors.

We are completing an error analysis (adapted from mathequalslove) where we determine what type of error we made (inattention, precision, computation, problem solving) and we also correct our error.  Over time, we’ll see trends in the error types we tend to make, and we can address these errors with strategies.  Becoming aware is the first step!

Strategies:

Inattention: PAY ATTENTION!  Check that you have the right numbers written down.  Take your time.  Check each line of your solution–cover up the rest of your work with an extra page so you can focus on one line at a time.  Use your finger to follow term by term.  Look for lost minus signs.

Computation: Remember PEDMAS.  Be careful about what brackets are telling you, i.e. (-4)^2 is different from -4^2.  Be careful about working with integers and fractions, sometimes we make errors if we are working too fast in our heads.  Check work with a calculator if you are prone to making errors.  Write all your steps so you can check them again later.

Precision: Correct units are important.  Writing your solution in a way that it can be followed is important.  Be sure to write statements introducing variables, and concluding statements.  Check back to the question to be sure you are answering what is asked.

Problem Solving: Read the question at least 3 times.  Check for understanding.  Draw pictures.  Ask for clarification.  Make assumptions and write them down.  Start with what you know.  Make connections to other problems you’ve done/other concepts you know.  You don’t have to know the entire path to the solution as you start.  Sometimes you see just a few steps ahead–that’s ok, keep going.  If you get stuck, you can always use another strategy–we have so many strategies!  Check back to the question a few times to be sure you are using all the information you have been given, and to refresh the problem in your mind.  If you are really stuck, take a break and come back to it.  Working through the questions you can do confidently FIRST, while you have confidence, is a good plan.  If your confidence gets shaken in the first 10 minutes of an assessment it’s sometimes hard to get it back!

We looked at polynomials today in grade 10, we made rectangles out of the algebra tiles that represent a given polynomial.  This example is x^2+5x+6.  We can see the dimensions of our rectangle are (x+3) and (x+2).

We looked at how the numbers in the equation are related.  To be able to make a rectangle we need specific values for the constant.

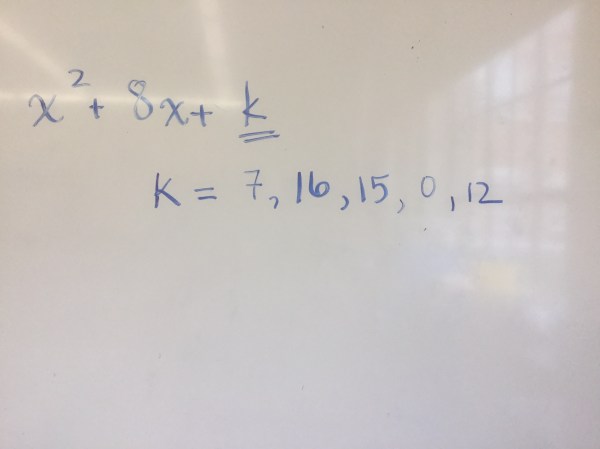
We know that the 8x can be arranged in a few ways, and each way leads to a different constant.

We can do the same if the constant is given but the number of x is unknown.  In this case, if the constant is 10, we look for the ways we can arrange 10 tiles in a rectangle.  We can do it as 1×10 or 2×5 so that will give us options of 11 or 7 x tiles to complete the rectangle.

Today is day 0, planting day!  We named our beans and watered them and are leaving them by the window.  We’ll be measuring their growth and comparing the two types of beans over the next month.

If we wanted to build a pyramid to fit inside our classroom, how many cups would be needed?

We made a function from our finite differences.  We then calculated the coefficients for each term using substitution.

We also saw how desmos can be used to do a polynomial regression

Our question today was: we have two cakes.  Period B ate some pieces of one cake.  Period C ate some pieces of the other cake.  How much is left?  Is it enough to offer to period D?

We counted 6/18 pieces eaten from one cake, and 6/16 eaten from the other.  We simplified fractions to 1/3 of one and 3/8 of the other have been eaten.

Knowing what we know about fractions and common denominators, we were able to solve the problem.  But we also looked at the problem visually.

If we divide a cake in three parts, and colour in one of those parts to represent 1/3, and the second cake we cut into 8 parts and colour in 3 of them to represent 3/8.  To compare the cakes and add up the pieces, we need the pieces to be the same size.  We divide each cake into 24 (3 one way and 8 the other).  We can then add up the 8/24 and the 9/24 to make 17/24.

We know that 17/24 were eaten, but to start with we had 2 cakes!  2 cakes have 48/24 pieces.  We know we have one whole cake left over, and 7/24ths of the other.

We looked at how to convert mixed numbers and improper fractions.

We looked at improper fractions for multiplying as well.  This visual model shows the multiplication of 3 and 2/7 by 1 and 1/2.  If you are not converting to improper fractions, you can still multiply, but you need to remember that it’s more complicated than just multiplying whole numbers and multiplying fractions together.  This grid shows all the multiplications broken down, and then added together at the end.

Good work today!