Exploring Exponents
Today grade 9s had a chance to build exponent models. We looked at representing x squared and x cubed using toothpicks and plasticine.
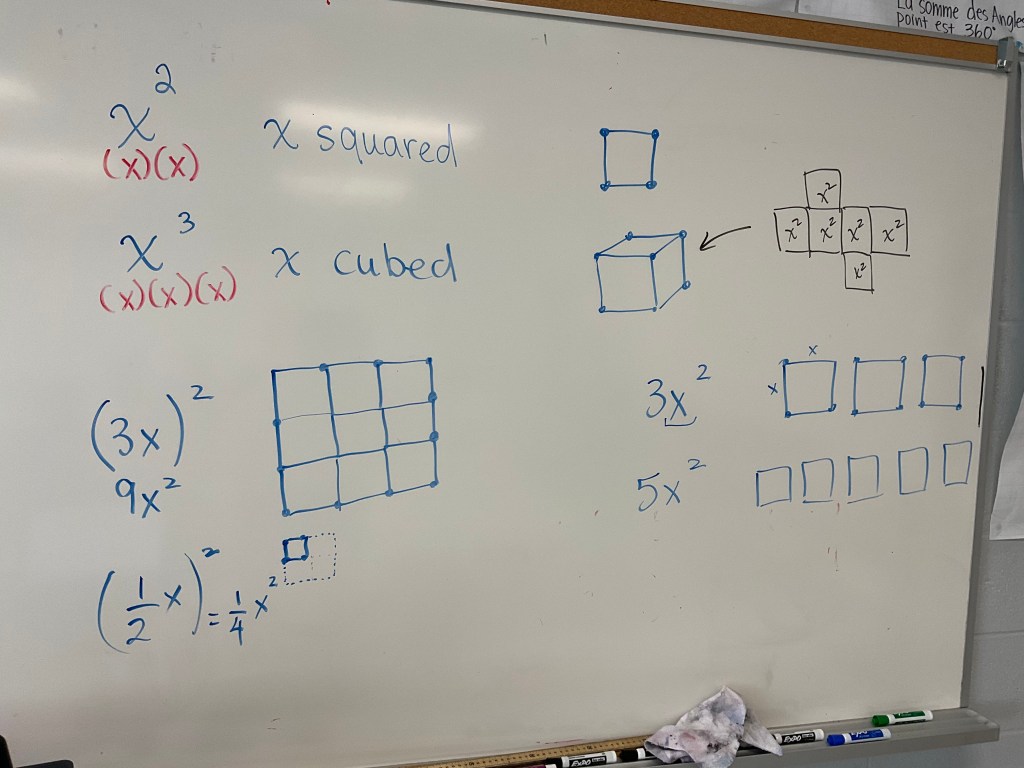
We noticed that anything with an exponent 2 is a square, and anything with an exponent 3 is a cube. We also noticed that the base of the exponent is representing the side length of the cube or square we make.
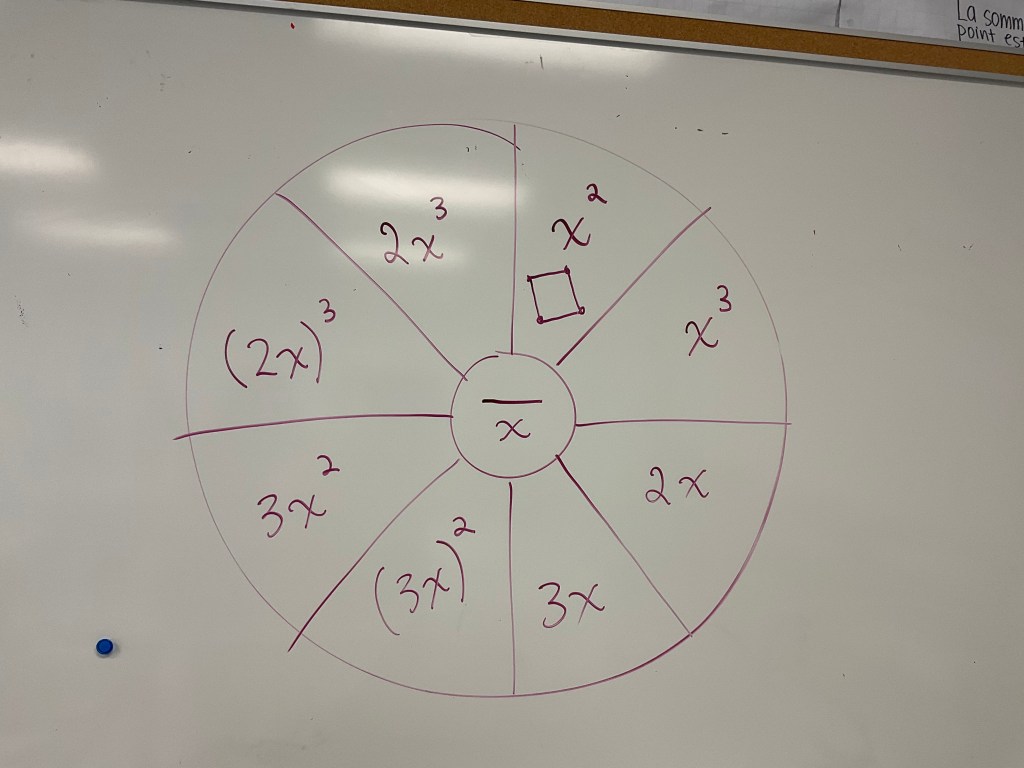
Since we were ready for a bigger challenge, I made up a spicy concept circle to try.
This one needed a bit more explaining. We looked at how x squared is a square, but also how it’s (x) times (x), how the length is x and width is x. This helped us look at (x)(y) as a rectangle with length x and width y. We introduced skewers as the y values.
We needed to talk about what an (x^2)(y) and an (x)(y^2) would be. We understood that they’d be 3 dimensional, but it took a while to realize that they’d be square based prisms, one with a toothpick square, and one with a skewer square.
We looked also at building (x+y)^2 which is something that challenges students in grade 10.
inside the (x+y)^2 we see an x^2 and a y^2 and also 2 rectangles that are both (xy). We can equate (x+y)^2=x^2+y^2+2xy.
Hopefully as we move forward with exponents and exponent laws we will have a sense of like terms, and simplifying, but also what happens if we multiply (x)(x)(x), and how we get x cubed. We’ll move from the concrete to the visual and abstract as the week progresses.
Exploring the Math of Sound
This morning I was invited to share an experiment with a grade 9 math class. It was inspired by the resonance that you get when blowing over the mouth of a bottle, and how that can change with more or less liquid (and thus air) in the bottle.
Each group needed the “sonic tools” app (free!) a bottle full of water and a ruler. They empty the bottle until they can blow over the neck and make it resonate. They record the frequency produced, and measure the height of the water in the bottle.
Then they empty a bit of water, and try again. We kept our data in a table, and then used it to make a graph.
We worked outside because it was nice out, and we could spread the groups apart a bit and we could empty the bottles on the flowers. When the class came back inside we put the data together into a big table, and graphed it on desmos. We graphed water height and frequency, and found a pretty strong positive non-linear correlation.
We looked at tuning our bottle instrument to a specific frequency, for example an A is 440 Hz, so we’d need a water height of about 17cm to make an “A” sound from our bottles.
The physics behind this is as follows: Air resonating in an air column that is closed at one end will resonate so a node is formed at the water, and an antinode at the mouth of the bottle. This will allow one quarter wavelength in the air column. The height of the air column will then be used to identify the wavelength of sound, often given the variable lambda.
We know that the speed of sound is determined by the temperature of the air it travels through, which is not changing for the experiment. The relationship between frequency and speed of sound is v=(f)(lambda). If we isolate frequency, f=v/(lambda). If the wavelength gets bigger (this happens when there’s a taller air column) the frequency will go down. This is an equation of the type y=1/x which we explore more in grade 11 math and also physics.
Converting Square and Cube Units
Our goal in MFM2P is that we will be able to convert square and cube units. We are slowly working on making sense of squares and cubes. We did a day of making squares and cubes on Thursday, and we revisited that today and made the transition from the concrete to the visual and then to the abstract.
We know that when the exponent is 2 we have a square, and when the exponent is 3 we have a cube. We know that what the exponent touches, either the x or the brackets, indicates the side length of the cube or square.
We next looked at a progression of questions involving drawing and reasoning about various cubes and squares.
We drew diagrams and looked at areas and volumes
We needed to remember prior knowledge of nets, and add to it ideas from when we built our models out of toothpicks.
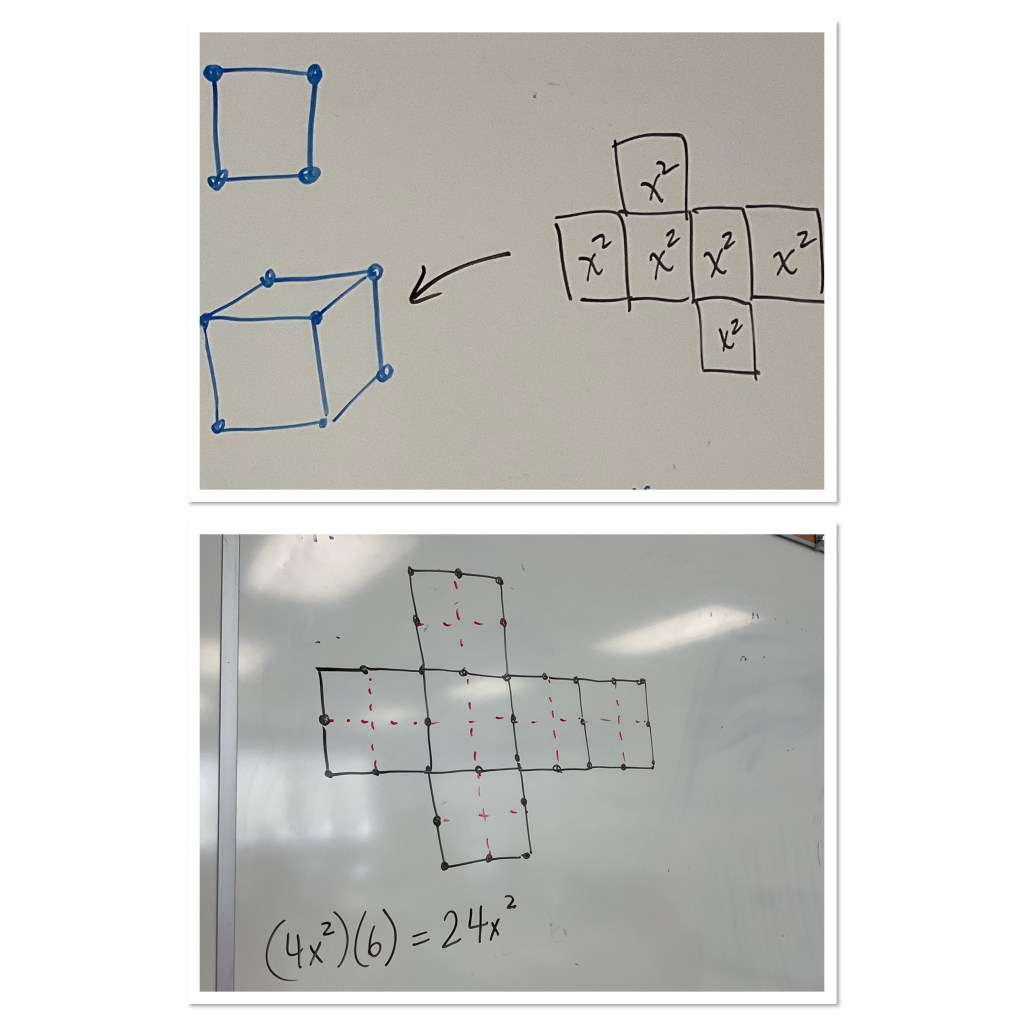
This led us to talking about how many square centimetres are in a square metre, which we can think of as (100cm)^2 since a meter has 100cm. We need to now understand that it’s 100cm by 100cm so the area is 10000cm^2.
We’ll do some more examples over the coming days during “algebra” and reconnect back to this again when we do volume and surface area calculations later on for “measurement and geometry”. Spiralling through a course allows for many chances to touch on the same material and review or solidify understanding.
Beading progress (almost done!)
We’ve finished up most of the beading, and now we are weaving in ends and gluing the hide to each side of our work.
We’ve started writing a little paragraph about the math that we see in the beadwork.
Happy long weekend! We’ll finish up the last of the work at lunch next week.
Building Exponent Models
Today in grade 10 we built exponent models out of toothpicks and plasticine.
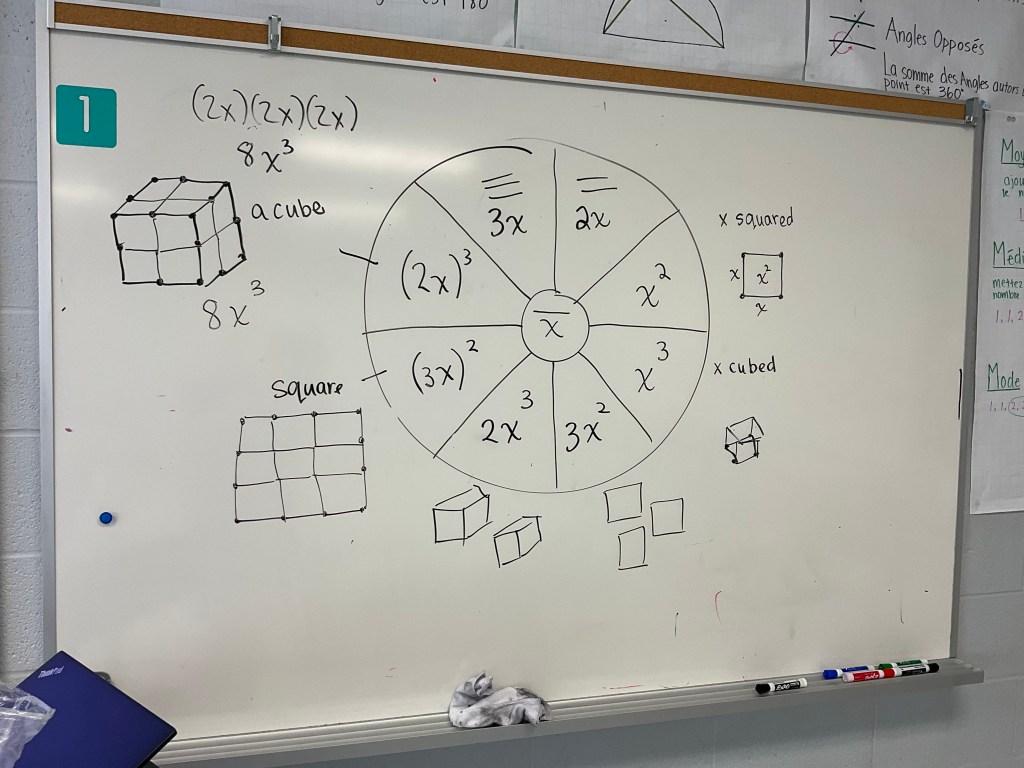
We are working on understanding that anything squared can be physically represented as a square, and anything cubed can be physically represented as a cube.
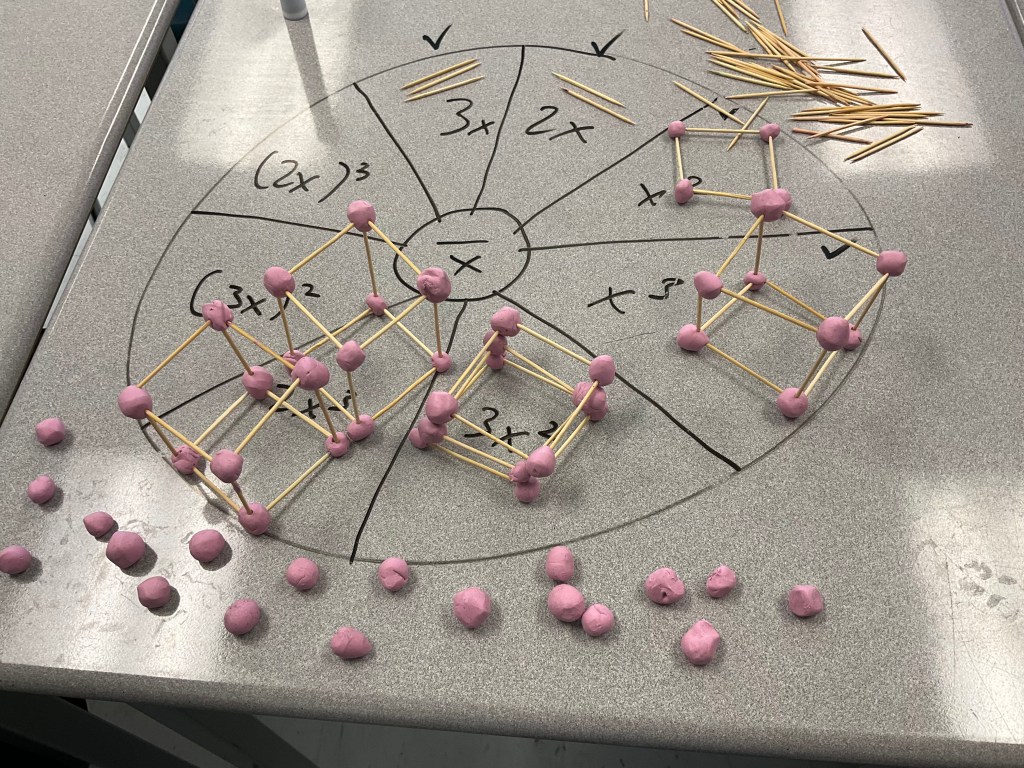
We noticed that the coefficient of the x squared or x cubed tells us how many there are.
If there’s a base that is a bit complicated, like (3x) squared, it means that the side of the square is 3 toothpicks long. That means when we build it we can see that there are 9 little x squareds inside. This means (3x)^2=9x^2
This group made one that wasn’t asked for, the little squares. The base of the exponent in that case would be (1/2 x) and the exponent would be 2 because they are squares. Since they made 4 of them there’d be a coefficient of 4 in front of the expression. We also can see that the 4 put together are equivalent in area to one x squared.
Here’s a good example of (2x)^3, and below there’s an attempt in progress of (3x)^3, which is always a big challenge to build.
We can use this kind of math understanding to help us when we convert square or cube units. Here’s an example: One cubic yard is equal to 27 cubic feet. We can understand this by knowing that there are 3 ft in a yard, and 9 cubic feet on each of the 3 layers of the cube to make 27 cubic feet.
We will be using this knowledge when we do volume and surface area questions in the future.
Angle Day!
Today we did some work with angles. We drew triangles and extended sides to make exterior angles supplementary to the interior angles. We labelled these angles then cut out along the lines.
This left us with 4 pieces. We took the triangle and cut out the interior angles, and put them all together. We noticed that for all the triangles it made a straight line, 180 degrees.
We put the exterior angles together and noticed that they make 360 degrees, or a full circle.
We did the same with quadrilaterals, and noticed what was the same and different. The interior angles of the quadrilateral add up to 360 degrees, and the exterior angles do too!
We had a look at this video to see the exterior angles always add to 360 degrees.
Next we looked at how we can solve problems involving angles. This one involved algebra!
It was energizing to see everyone involved and learning before a long weekend.
3 Act Task
Today I was invited into a colleague’s grade 9 math class for a 3 act task that we led together. 3 act tasks start with act 1 to pique the interest. Students watch the video and write down what they notice and wonder.
Next comes Act 2, where more information is shared, and students use the information to solve a problem.
In this case we are figuring out how long it takes for the candle to burn out fully. Students use the data, in tables, and graphs and use logic to attempt to solve the problem.
This class has recently been working on scatter plots, so we encouraged a graphical representation to solve. Sometimes this can be done by loudly praising the graphical representation of one group, and others will latch onto that methodology. We worked on making sure axes were well scaled, and had labels, and then groups realized that they’d need to extend the trend a bit through extrapolation and a line of best fit. Some groups needed to extend beyond their graph!
One group didn’t want to scale their axis in a conventional way. We worked with them to see how their graph could still help them solve the problem.
In the end, when all groups had sorted through their responses, we consolidated their work, pointing out excellent communication, and including vocabulary about trends that they’d been using recently. At the end of class we watched the final act video which revealed the conclusion.
This task shows the use of a graph and extrapolation to solve, which made it a great fit for the recent topics.
I look forward to working with this class again soon!
Beading Progress
We worked hard at our beading projects again today. We are making solid progress!
Now that we know what we’re doing, it’s quite a calm meditative activity. We don’t have to remind ourselves as frequently to watch our energy. We need to make sure we are doing beading with good energy and intentions.
We’re making really interesting patterns too. Each one is unique and we’ll have lots of math to discuss when we get to finishing our projects.
Tomorrow most of us will be weaving in ends and gluing to prepare for attaching hide to make bracelets or keychains.
Beading Progress
Today we learned how to get started with our beading projects. We used our patterns to decide what beads we need. We put the first 11 beads on the needle and learned how to thread them to attach them to the warp threads on the loom.
Next we gave it a go! We ran into our fair share of frustrations: a loom came unthreaded, some knots happened where we didn’t want them, beads fell off the thread, needles came undone, but all in all we made good progress, and we kept calm when things were challenging.
It’s pretty neat to see what progress can be made in one day. We look forward to continuing the progress tomorrow. If all goes well we can be finishing them up before the PA day on Friday.
Great work grade 9s!
Multiplication Fluency
We’re working on multiplication strategies these days, and we got out the base 10 blocks to model some multiplication. We did 15×6 to start with.
Some students made 6 groups of 15, and then counted. They knew they had 6 groups of 10, and 6 groups of 5, so the total was 90. Others used doubling and halving with this question. They doubled the 15 to make 30, and they halved the 6 to make 3, then they multiplied 30×3 and got 90. They then used 9 rods of 10 to build the 90, or used 100 and a negative 10 rod to get back to 90. It was neat to see the different ways students approached the problem.
We next looked at 26×15 to see if there were different approaches.
One group built a rectangle thar had dimensions of 26 and 15. We can see (top right) that this gives us a nice area model to work with. We can section the rectangle by friendly numbers and then calculate the small areas and add them up. Another group kept using the doubling and halving. They doubled the 15 to get 30, and halved the 26 to get 13 then did 13×30. Some did 13x3x10 to make it easier. Either way you get 390. One group made the 390 in a 3D shape and another made it in a flat rectangle, starting off with 400 and removing one by using a negative 10 rod.
I’m really glad my students are getting braver and are excited to share their strategies. Here’s one student’s area model. We needed a small correction, but it was a great way to show our work.
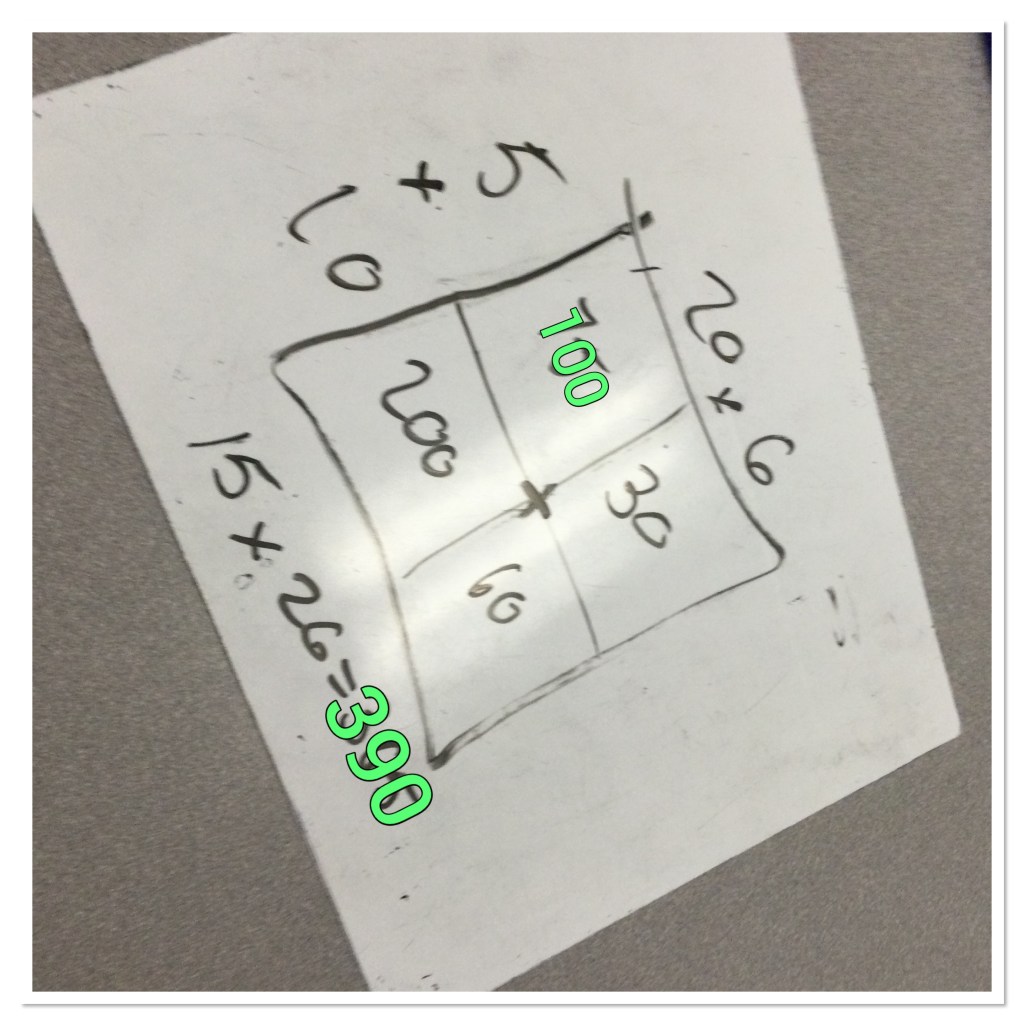
Next we used our multiplication strategies to work through a number string, doing one question at a time sequenced in an order to help us get to more complex problems by using work done in prior questions.
We’ll keep working on these strategies. It’s fun to see the learning happen!
Ms. Bearse's Site 