Introduction to Loom Beading
Today we had the pleasure of learning from Jessi from the Indigenous Program Team at the board office, who brought some historical and cultural perspectives about loom beading, and some teachings to share with us before we embark on our project.
Over the next few days we will be planning and beading a bracelet/bookmark/keychain, and then reflecting on the math that is present in the work, and the other skills that we learn during the process.
Today we got our beading templates, and started to plan. Tomorrow and Wednesday we will be doing the beading, and then we will finish things off on Thursday, and let the glue dry over the long weekend.
It is always such an exciting time to see what our students can do creatively, and then analyse mathematically afterwards. More pictures will follow in the coming days.
Introduction to Algebra
Grade 10 applied students got their first test back today, and we started learning a new topic: algebra.
We got out the algebra tiles and remembered what we did in grade 9. We built polynomials, then added them.
We simplified using zero pairs, and worked on using vocabulary words to express what we made, and what the result is.
We’ll be solving equations next week using tiles. Hope that we’ve jogged enough memories to have a solid start on Monday. It’s so good that our grade 9 classes are using manipulatives so consistently now, so I know that my 10s will all have seen and used the tiles before. We’ve worked hard to build a solid grade 9 program which we are now spreading into grade 10. It takes work, but it is so worth it!
Correlations, and beans?
My grade 9s really wanted a “fun friday” today, so we did an activity involving everyone getting up, mixing mingling and taking off their shoes. It ended up with a nostalgic discussion that was all about beans. A memorable day for all!
The goal of the lesson was to make a scatter plot and talk about correlation, and to show how google sheets can be used to make a graph and see a trend-line and an r squared value, and then be used to make predictions.
We taped ikea rulers to the wall, then took turns being measured. We stepped on rulers and measured our foot length too. Then we made a graph to see if it’s true that you can guess someone’s height by looking at their shoe size.
In our class the trend is pretty weak. The r squared value is 0.53, but we can see that height correlates a bit to foot length. The larger the foot the taller the person, in general, but we wouldn’t be very confident in the height of someone if we just saw a foot print.
We talked a bit about how this graph really only represents grade 9s, and with a small class, and some absences, it is not even a really good sample of the whole grade 9 population. We noted that grade 9s are in the middle of growth spurts, and that this likely does not represent what a graph of adult height and foot length would be.
We discussed vocabulary about trends (postivie/negative, strong/weak, linear/non-linear) and we made lines of best fit by hand, and with technology on google sheets. The final step was to chat about making predictions using our trend-line, and how some predictions are interpolation (inside the data) and some are extrapolation (outside the data).
I then told the class a story about when we were back at kcvi and had deep windowsills. My classes used to take advantage and grow beans on the windowsills. We’d turn it into quite a project. We used the dry beans to explore counting, and then we germinated the beans in paper towel and water in a baggie for a few days. We looked at the fraction that germinated and the fraction that rotted.
we planted the beans in small paper cups and cared for them as they sprouted above the soil. The plants were measured daily, and data tracked in a table. We grew kidney beans and black eyed peas, and compared their growth over the first week or so that they sprouted above the soil.
Next step was to graph the bean data in scatter plots, we could compare growth rates of different types of beans and make predictions from the data about the height of the bean at the end of a month of growing.
The trick is that the beans start off with quite a linear trend for the first week, with a very different growth rate between kidney beans and black eyed peas. These plants do NOT maintain their linear growth though. They are bush beans which have a maximum height. Students predicted bean plants that would be about a meter tall after a month of growing, but they maxed out at maybe 30cm.
By then though we were attached to our little bean garden, and we kept watering them and caring for them and many times the bean plants would flower, and then after the flower dropped off a baby bean was there, growing and producing new bean seeds inside.
After me doing some show and tell (search for beans on this site and there are lots of progress pictures), my students were disappointed in our sleek windowsills and wanted to grow beans. I happen to still have a bag of dried beans in the closet, so many went home today with some black eyed peas in their pocket and dreams of making a bean garden of their own. We’ll see if any are successful.
It ended up being a pretty fun Friday after all!
Solving with Relational Rods
Today I was invited to see a lesson about solving equations using relational rods. This approach is new to me, and it was fun to learn alongside the students. Here we represent 20, and we know that when we split it into “m” pieces, the values of the pieces is 5. So we use 2 of the ten-rods to build 20, and we see that we need to split it up into groups of 5 (the light yellow is the 5 rod). There will be 4 groups, so m is 4.
Here’s another question: 4 groups of something equals 8. We know that the 8 rod is brown. We can use trial and error to find out what rods equal 8 when we use 4 of the same. The red rod works, and has a value of 2.
Here’s a more complicated one. 2 groups of something, minus 1, is equal to 5. That means 2 groups of something is one bigger than 5. 2 groups of something is equal to 6. The 5 rod (yellow) plus 1 (white) is equal to 6 (dark green). If we need to find a rod that can fit 2 into the space of the dark green, it’s the light green one, which is 3.
Here’s another: 2 groups of something, plus 6 equals 14. We build 14 from a 10 rod and 4 one rods (lots of other options we could have done). We know that 6 is a dark green. I need to now fill on the empty gap with 2 equal blocks. We can use the purple which is 4. Z=4
Here’s one last one, that was interesting….there were 2 ways to solve. The first way involved building 27. We used 2 ten rods and a seven rod. Then we used a 9 rod (blue) and had to fill on the gap with 2 equal sized pieces. Those pieces happen to also be 9s. We know a=9.
If we had built the 27 in a different way, we can see another property. We can build 27 as 3 nine rods (blue). Then we can build the 2a+9, so we put a 9 on top. We can see that on the top and bottom we have 9s, so those 9s are not needed…and can be eliminated. Now we just need to find 2 pieces that are equal to 18 total, which we can easily see are 9 and 9.
We followed this up with a bit of practice using algebra tiles to solve equations as well. It was a great learning experience for me.
Would you Rather?
Today in my MFM2P class we did some work on being a good group member. We talked about what we do when working with a partner. We share the marker and both contribute. We use clean language that is encouraging, respectful and positive. We ask good questions and learn from each other. We write our thinking so other groups can learn from us, and we listen with our ears AND our brain.
We did some review of graphing lines, to close some gaps made visible on yesterday’s test. We worked on graphing y=2x+4, y=2x+6, y=2x, and y=-2x+3. Then we looked for intersection points.
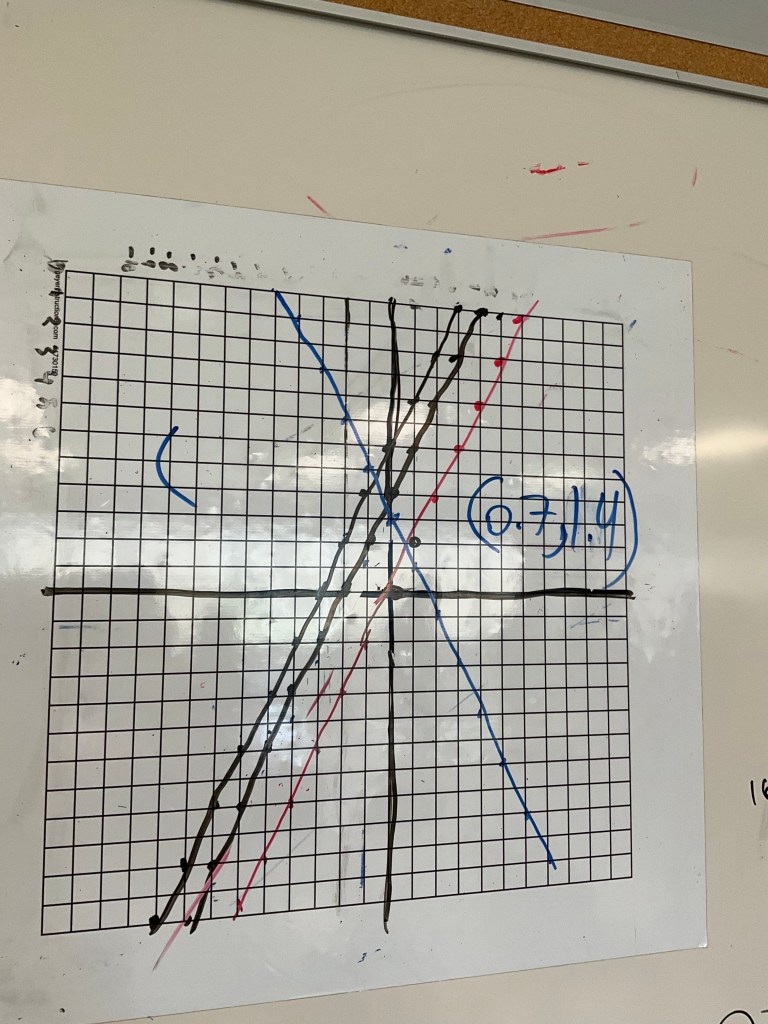
We noticed what makes lines parallel, and what positive and negative slopes look like, and what the constant in the equation means.
The next challenge we had was a would you rather challenge.
I had never tried this question before. It was a good chance to talk about what a pound is, what quarters and dimes are, and what information we’d need to solve the problem.
Students dove into the problem solving once we looked up the weight of a quarter and a dime is in ounces, and what a pound is in ounces. This task uses unit conversion and proportional reasoning. It’s fun to see how groups worked together to tackle the problem.
Spoiler: the value is about $25 in either case, which is pretty cool! We decided having that in quarters would be easier to manage.
There are lots of sites with would you rather questions prepared already, a quick google search can help you find your next mathematical challenge.
It was a good day with lots of teamwork, positive language, and participation. I hope we continue with this energy moving forward.
Solving with Algebra Tiles
My grade 9 class this week has been working on solving equations. We used algebra tiles to help us visualize what we are doing, and to help us choose our next steps. Here are some examples of the process.
We represented each side of the equation, and drew a line where the equal sign is. We know that both sides are equal. Our goal is to get the variable tile alone on one side. We can do that a few different ways. Here we decided to create zero pairs for the +2 which is on the same side as the x. This will annihilate the +2, and we will have the x alone.
We have to do the same on both sides to keep the equation equal.
Here’s another example. We have variables on both sides here, which we are not thrilled about. To annihilate the -x on the right side, we place a +x to create a zero pair. We must place +x on the left as well to keep things equal. Next we place +3 on both sides which will create a zero pair with the -3 which is on the same side as the x term.
We end up with 3x=8. The next step is to split the 3x into 3 groups. We want each x to have its own group. We split the 8 up into 3 groups too. This is tricky since it doesn’t divide equally. We will have 2, and then we need to cut each of the little blocks remaining into thirds. Each group will get 1/3 of each remaining block. Wr end up with 2 and 2/3 as our answer for x.
Another way to visualize this is to say that we have 8 blocks that we want to divide into 3 groups, and we represent x as the fraction 8/3, which is equivalent to 2 and 2/3.
We have worked on representing and solving lots of equations. Some students will use the tiles for quite a while. Others can make the connection to an algebraic representation, but the understanding remains that we use zero pairs and opposite operations to isolate x. Using the tiles helps us remember what our like terms are, and we physically see both sides all the time, and we know we must keep them equal by doing the same thing on both sides each time.
Angles in a Triangle
Today we looked at angle sums in grade 9. I don’t have a before picture, but I cut out some triangles, labelled their angles A,B,C, then ripped them up to put the angles all together to form a straight line.
We did the same thing for a quadrilateral, labelling the angles, ripping it up and placing the angles together to form a full circle, 360 degrees.
Next we looked at exterior angles, and how they always add up to 360 degrees. You can do this with paper too, but I hadn’t been careful enough when I cut out the shapes earlier. This video also gets the point across, and when played in a loop is quite calming and meditative.
We then started to solve equations to find missing angles. This is our introduction to solving, which is a change to my previous sequence. I think it’s a nice introduction since the values we are finding are all positive, and we can practice writing equations all in context of solving for a missing angle.
Test Day
Today was test 1 for my grade 10 applied class. We tried doing “test talk” for the first 5 minutes. This is a technique I saw Howie Hua talk about in this video.
we put pencils on the floor, and with test in hand have 5 minutes to look through it and talk with others in the class. This strategy helps to lower anxiety levels, encourages people to read through the entire test before writing, and also values the collaboration that we do each day. Nothing is written during this time. After the 5 minutes is up, it was back to regular test protocol, quiet individual work.
I also handed out some smooth stones which is something I’ve done for years. It’s a good fidget, and also something calming to hold onto.
Some students used tiles during the test to help with patterning. Others just wrote and drew pictures.
for a first test I think it went pretty well!
Shrinking Ropes
Today we did a task involving knot tying. We had several lengths of rope in different thicknesses. We tied overhand knots in the ripes and measured after each knot was tied.
We kept track of our data in a table, then graphed it on paper.
While not perfectly linear, it’s a really strong fit.
We answered some questions about the relationships, and related what we saw to our recent studies of linear and quadratic patterning and relationships.
I was impressed at how self directed my students were today. We were on task for almost the entire period.
Multiplication Fluency
We worked on a multiplication fluency task a little bit today. We used 24 snap cubes to build as many rectangles as we could. They needed to be solid rectangles.
It took a while to figure out how many different options there were, and why we couldn’t build one with a dimension of 5. We came to a conclusion that the length and width of the rectangle multiply to 24, and that wont work for 5.
Some groups were interested in making 3D prisms, and we made the connection that the dimensions would be (2)(2)(6) or (2)(3)(4) and in both cases if you multiply those 3 values you get 24, which represents the volume of the prism.
Another group went rogue and started building a giant rectangle, and then figured out how many blocks they’d need to build it. That took some serious multiplication skills.
We’re getting better at using manipulatives without them ending up all over the floor. We have a well established “no throwing” rule, and we are working on helping care for our materials and our space.
Ms. Bearse's Site 