Patterns to Graphs
We’ve been working on building patterns in MFM2P, showing linear growth. We are comfortable with the idea that figure 0 is our constant, and that there will be a consistant change between all the subsequent figures.
Today I gave groups a pattern rule to build. We made the patterns showing figure 0, 1, 2, 3, 4. Once that was done, we lined up all the blocks in figure 0 along the y axis of our graph. We’re using 1 inch tiles and 1 inch graph paper so that the squares line up perfectly with the grid. We make figure 0 into a stack, and then put a dot on the top left corner of the stack. We do the same thing for figure 1, making a stack right next to figure 0 and then adding a dot at the top left.

We changed colours of markers and then did the same thing for a new pattern rule, with a goal of superimposing the graphs to compare the lines. This instruction was a bit complicated for some groups to follow, but we all got 2 graphs drawn in the period, and learned a bit about the rate and the constant while we worked.
The next day we used our graphs to do consolidation. I helped with the superimposition of the graphs, sliding one graph onto the next. We then compared slopes, talked about steepness.

We talked about what negative signs do, if the rate is negative, or the constant is negative. We talked about intersection points and how to show that a point is on both lines.

We looked at making a lot of parallel lines. We repeated a lot of times that parallel means “same slope”. We noticed that we don’t have to write +0 at the end of the equation when the constant is 0. These 2 lines cross at the origin (0,0).

We noticed that if the constant is the same for 2 lines it will be the point of intersection. We also noticed how we could do the same task but with quadratic relationships. Here there are 2 intersection points between a line and a parabola.

By the end of the 2nd day we are getting really confident with out graphing skills.
Intro to Pseudocode
I had the chance to work with a grade 9 class this week to introduce pseudocode to them. Their teacher had a neat idea to start us off: write the steps for tying your shoes. We had several attempts which were not highly successful, and then edited our directions to add more details.


We followed up this task with a video of how to make a peanut butter sandwich.
Finally we started to put some pseudocode in the right order like a puzzle.

once we had the code we debriefed what the instructions meant, and what the key aspects of code are (variables and calculations and what to display on the screen).

This is a nice start to understanding code, and a preview about calculating area and perimeter. It was a fun active lesson with lots of participation and giggles.
QSLMA mini conference 2025
I was thankful to have had the invitation to present at the QSLMA mini conference this year. My presentation was about Creating Brave Spaces in your Math Classroom (slides here).
We talked about how we start our term at KSS focusing on establishing norms, and encouraging participation, including lots of examples of noticing and wondering, and using various low floor high ceiling thinking routines and tasks, like which one doesnt belong, slow reveal graphs, dot talks, 3 act tasks and more. (The slides have more information and links to these sites).
The most fun part for me was when we did a cup stacking task. The challenge was the same as I had brought to my classes this week: to build a stack of cups as tall as me.

We had a few ways to do it. It was neat to see the variety of strategies. The triangle stack extension idea had people working in different ways again. This group made a flat triangle, so each row was one less cup than the row below.

This group decided to try something I’d never tried: a triangle based pyramid of cups. (They had really wanted to have unicorn emoji faces, but my options were limited!)

We worked on modelling the growth for this stack, and based on 3rd differences being the same, we think it is cubic. We start with 1 cup, then add successive triangle numbers as each row is added. We know that triangle numbers are a quadratic pattern, so it makes sense that it is cubic. Desmos can be used to do the regression for us.
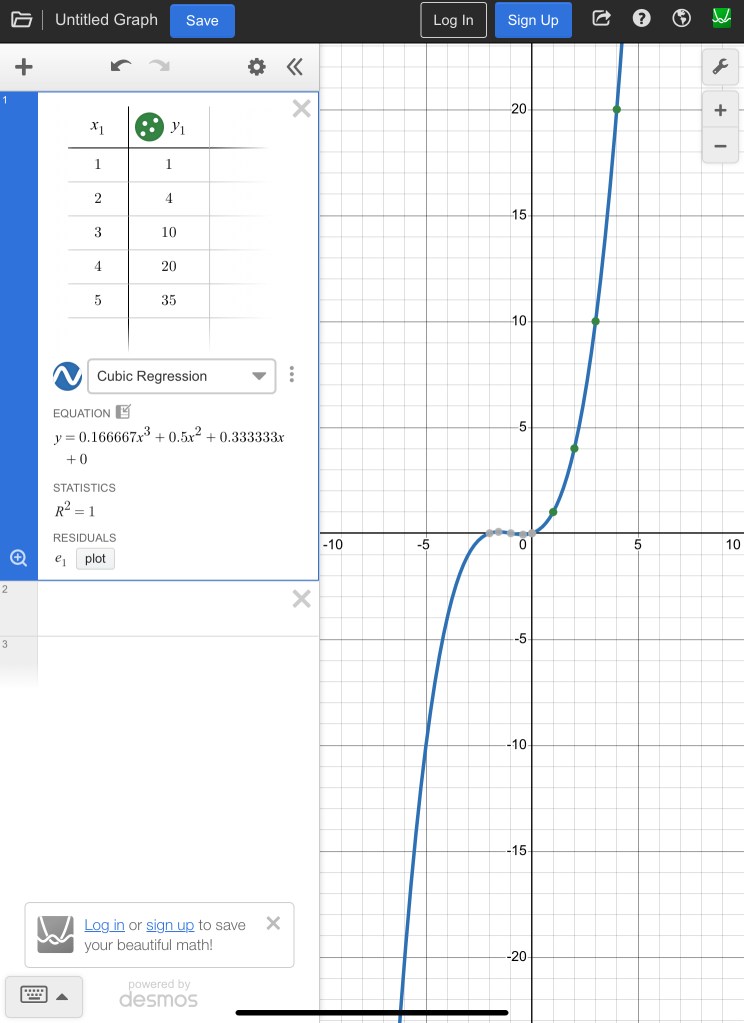
Thank you to the enthusiastic participants for the session. It was great to have so many teacher candidates in the room.
Cup Stacking Part 2
Today we tackled the challenge of building a triangle stack of cups that’s as tall as me. I’m 5’6” which we converted to 66”. Since the table is 30” tall the stack needed to be 36” tall.
We used our prior knowledge that the cup is 4.3 inches tall and divided 36” by 4.3” to know that there should be 8 rows of cups in a tower as tall as me.
We also noticed from experimenting that a triangle stack of cups has the same number of cups across the base as the number of rows high.

There will be 8 in one row, then 7, then 6, then 5 all the way to 1. Some knew a quick way to add these numbers up.
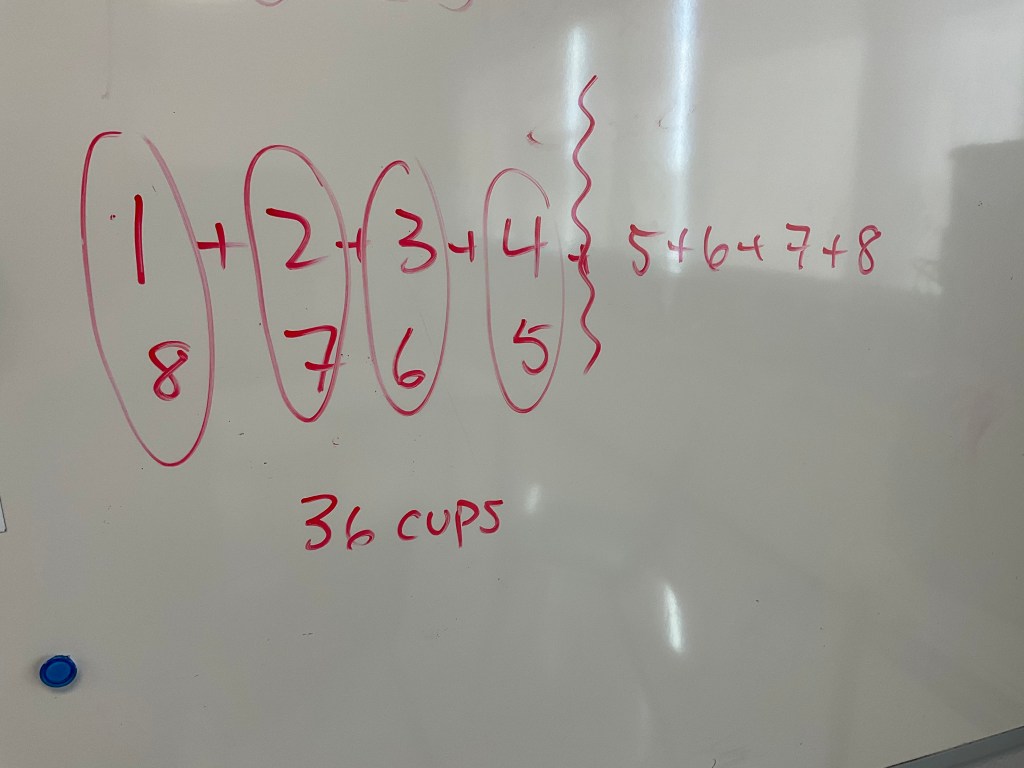
The next challenge was to build a triangle tower from the floor to be as tall as me. There were some quick calculations by some, and some intense stacking by others. It turns out that we needed way more than the initial estimate of double the number of the desk tower.



While the building was going on in one corner of the room, the rest of us were exploring what Desmos could tell us about the pattern we noticed.
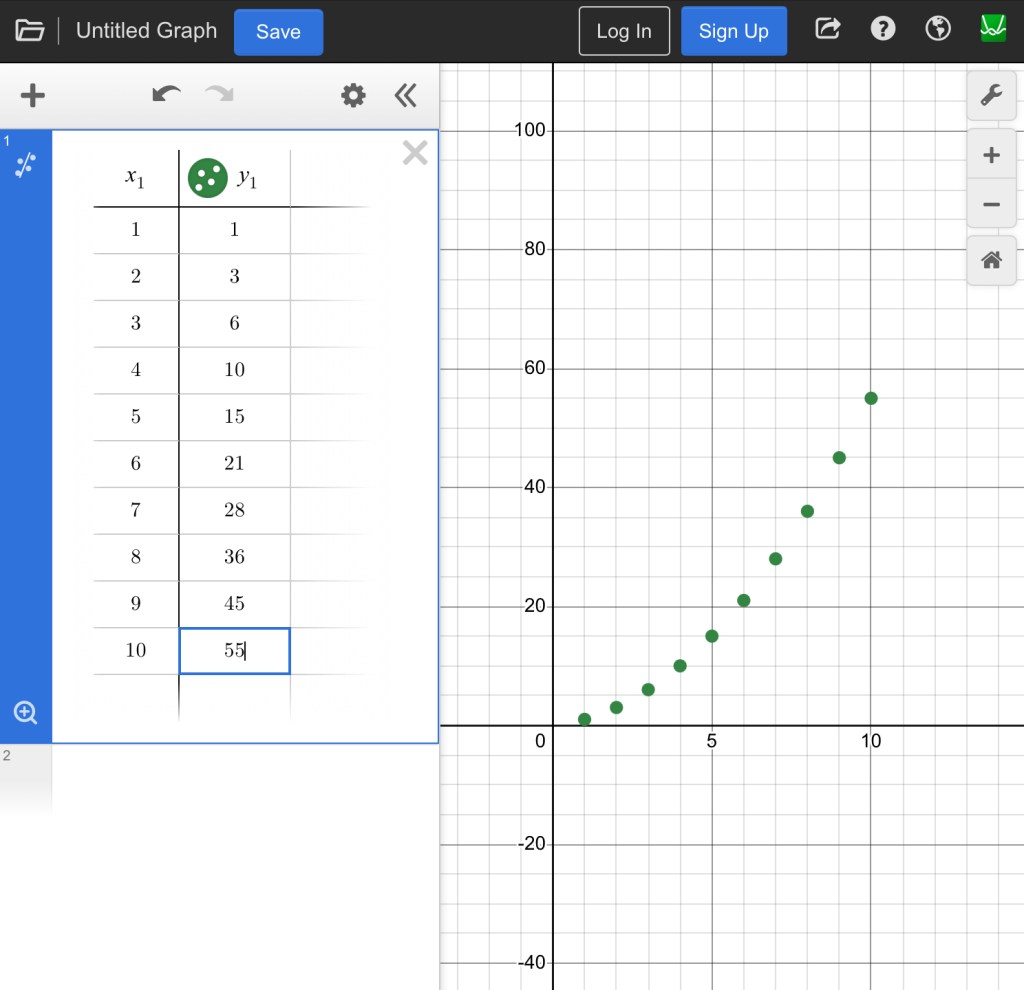
We used x to represent how many rows tall our triangle would be, and y represents the number of cups used in the triangle. We could tell by looking at the 1st differences that it is not linear. The dots also do not make a straight line. We noticed that the 1st differences, or the “change” changes by 1 each time. When we see a second difference that is the same, the graph is quadratic so we can do a quadratic regression. Desmos has made this much easier now with a button at the top left of the table window.
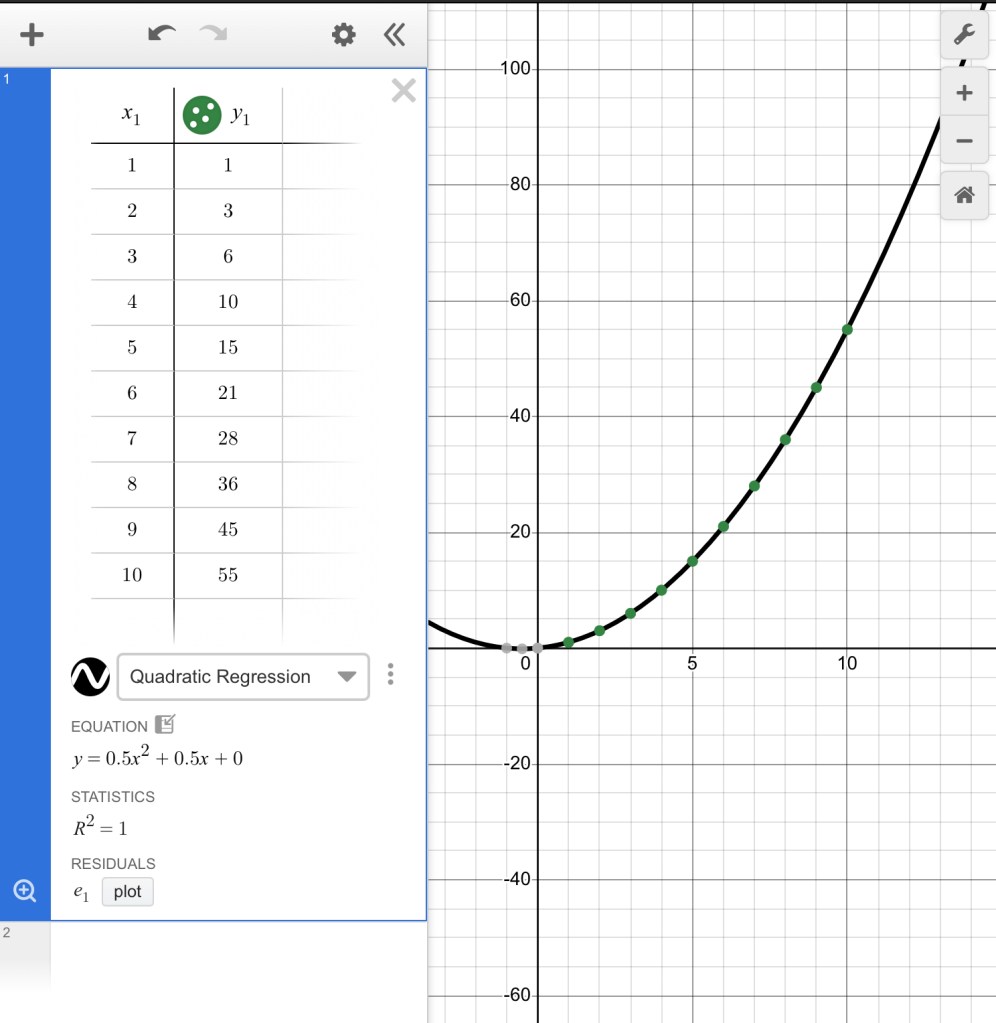
We need to choose quadratic regression, and then the equation is given to us. We can use the graph as well to solve problems. If I want to make a triangle stack that is 15 rows tall, I can make x=15 then check to see the intersection of that vertical line and the graph.
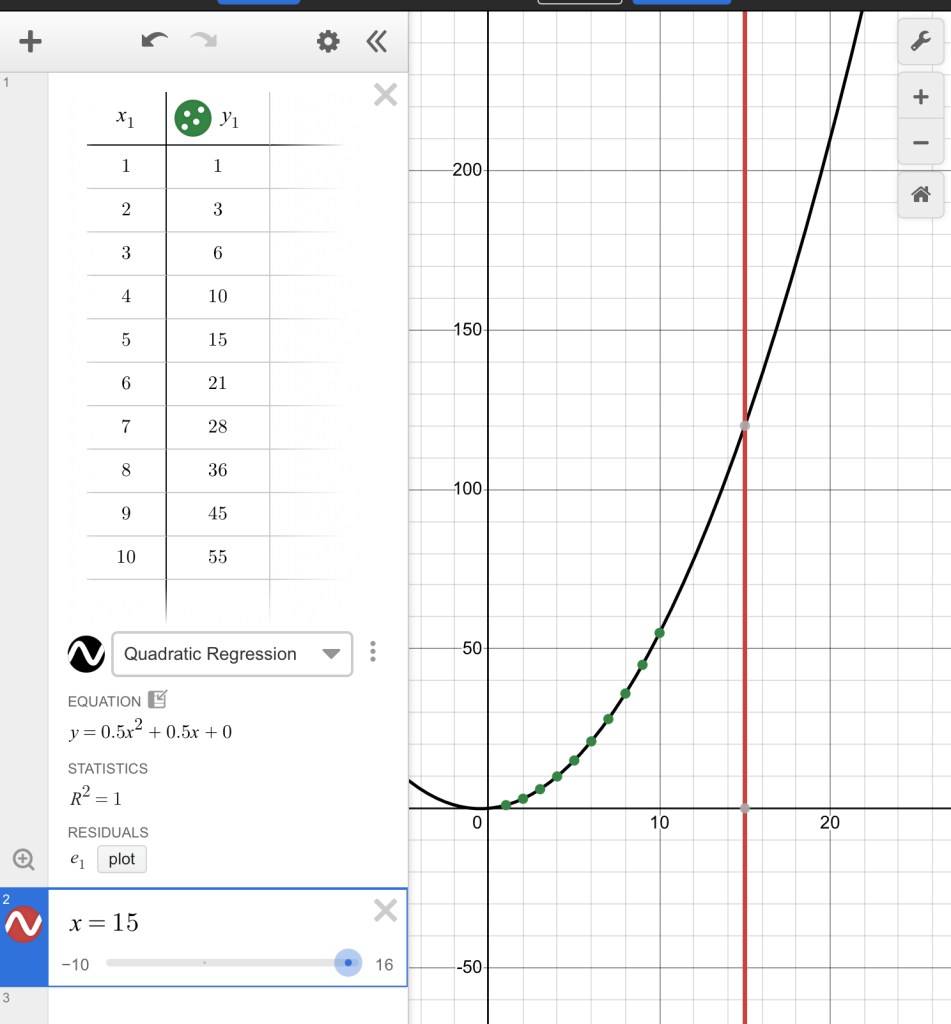
We need 120 cups to make a 15 row tall triangle stack.
We will use Desmos often this year as we explore different relationships. It is a very powerful free tool.
Today we had fewer minutes off task, and less breakage of the cups. There was a pinky swear contract for good behaviour at the start of class which was respected, for which I am very thankful.
Cup Stacking
In grade 10 applied we are working on patterning and representing relationships. To build context for equations we did a cup stacking challenge. The goal was to figure out how many red solo cups were needed to make a stack as tall as me. The challenge is that I gave them only 3 cups to start with.
Groups measured the cups, and decided how to stack them.

My height is 5’6” so there was some unit conversion needed. Many groups chose to work in inches, and others chose to work in centimetres.

Once there were calculations, or reasoning that was justifying the number of cups needed, I handed out the cups that they requested and they started stacking.

We saw some pretty accurate predictions! The next challenge was to figure put how many cups would be needed if the stack started from a desk instead of the floor, and then if we used small cups instead, on the floor and from a desk to make stacks as tall as me.

We are able to represent the growing tower height in a table, noting that each increase of one cup is the same increase in height each time, so it will be linear growth.

We consolidated our work together showing how the table and graph can also be used to predict the number of cups needed to stack to my height.

This task was challenging because of the group work dynamic. We are still working on our teamwork and staying on task. Also the cups are light weight and towers will tip over, causing quite a noise. I was glad of 2 volunteer Sr. students in the room who helped out.
Our next challenge is to make a triangle stack of cups as tall as me, if we have enough cups. One of my students has already done some predictions and calculating to solve that challenge.
Order of Operations
We’ve been working on integer operations and order of operations this week. We’ve been practicing the norms of working together in random groups at whiteboards around the room. We’re practicing listening carefully when I say the questions out loud, and getting right to work.
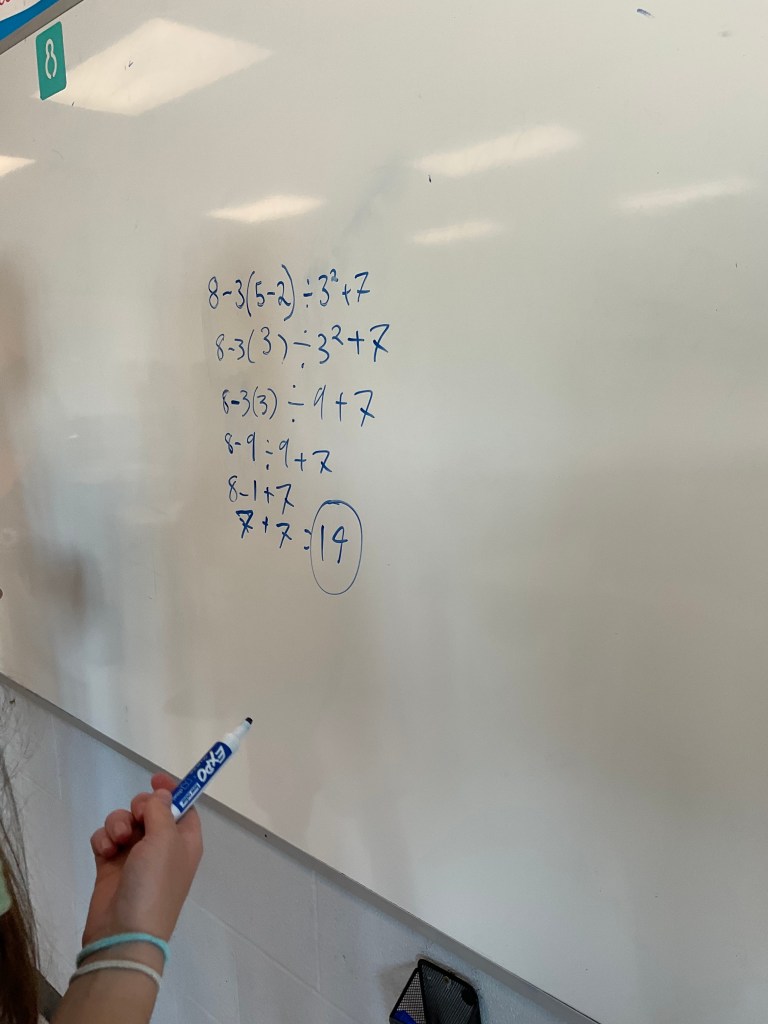
In our consolidation today the focus was on the correct order of the operations, and also we worked on clear notation, where each step is written out to show what is changed.
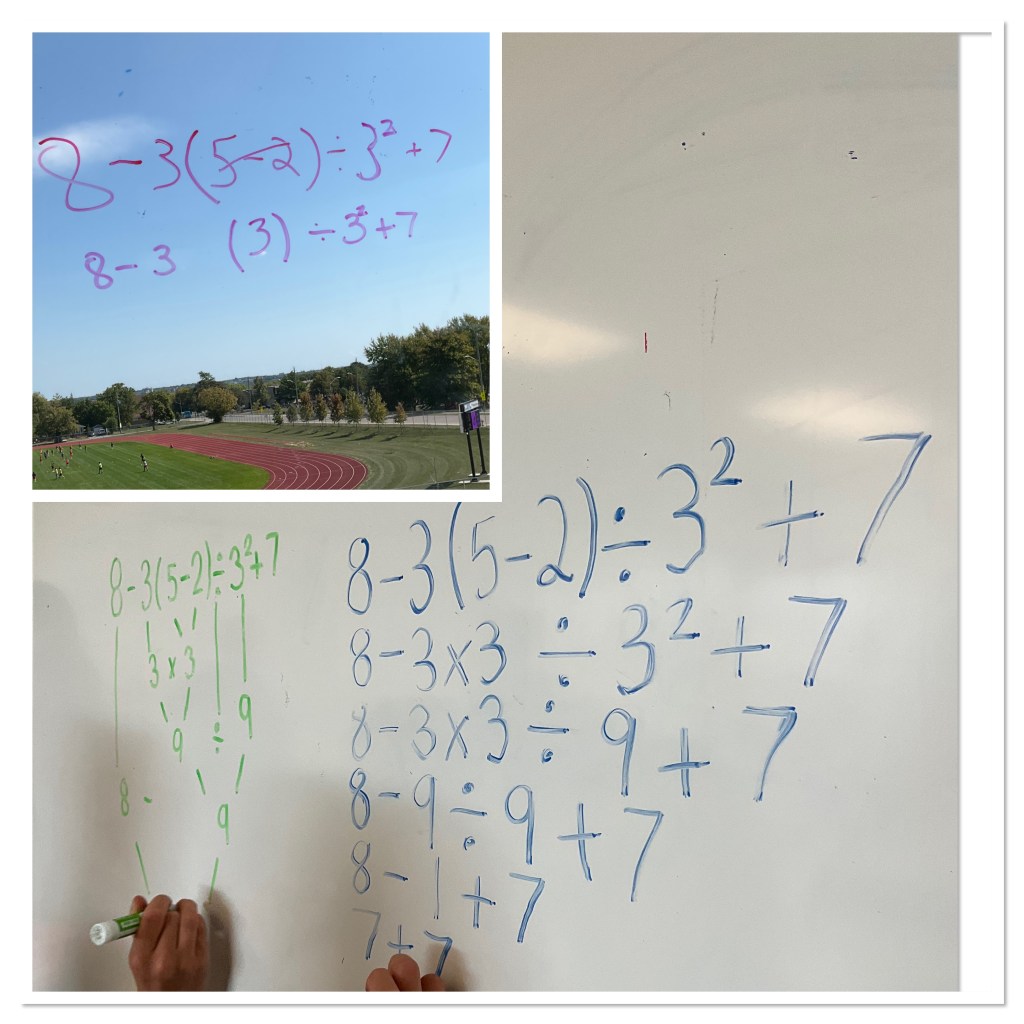
We had quite a lot of unconventional notation which sometimes makes some operations get lost along the way.
We’ve got lots of time to keep working on our notation and our order of operations skills.
We also have been enjoying this excellent song to help us remember the order of operations.
Bucket of Zeros
Today I had the chance to work with a grade 9 class on integer adding, subtracting and multiplying.
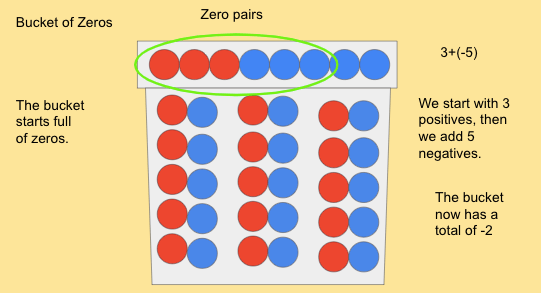
The bucket of zeros includes understanding of zero pairs.

When adding, the tile are all combined, and zero pairs identified, and the answer will be any unpaired tiles at the end.

Subtracting involves using the bucket a bit more. There are animations in my slideshow which show how groups are taken away, including from the bucket, and how by using zero pairs the result is simplified.
The bucket can also be used for questions like -3(2), which can also be written as 0-3(2), which would mean we start with zero, then remove 3 groups of 2. The addition of the 0 in the front of the questions helps to ground us with our original bucket of zero.
It is with this type of task that I can explain to people why a negative times a negative is a positive, or why a negative times a positive is a negative. It brings conceptual understanding rather than just memorizing some rules.

It was great to see students engaging with manipulative tiles at their desks and building confidence with this new thinking routine.
Locker Task
Today in grade 9 we challenged ourselves to solve a problem. We experienced productive struggle and persevered for the entire 70 minutes of class time on this one problem.
Here is the prompt:
There are 100 lockers and 100 people. The first person walks past and opens each locker. The 2nd person walks past and closes every 2nd locker. The 3rd person walks past and changes the state (open/closed) for every 3rd locker. This continues with the 4th person changing the state (open/closed) for every 4th locker etc. When the 100 people have walked past the lockers which lockers will be open?
Students worked on representing the problem in a manageable way.

some used 1 and 0 to represent open and closed. Others used mark and no mark to represent open and closed, and other groups used colours to track the open and closed lockers.
It took us a long time to go through the task without making mistakes. Some groups decided to shrink the problem and work on a case of 30 lockers and 30 people.

We eventually landed on the following open lockers:1,4,9,16
From there, some students saw that the numbers increased by increasing amounts in a predictable way. Others saw that these numbers are all square numbers.
The next question is: why do these lockers stay open?
We talked a bit about how we used our multiples to open and close lockers, but also we saw that the factors of the numbers represent the people who touch the lockers to either open or close them.

All of the square numbers have an odd number of factors (since the middle factor represents the square), so the lockers are open, closed then open again.
I was impressed by the stamina that was shown in the class, and how they were keen to explore the problem in a few ways, and to make use of their skills in factors and multiples in the problem solving.
Group Work in Grade 9
A great way to start a conversation on group norms is through Sarah Vanderwerf’s 1-100 task. Students are given a 1-100 page with numbers all over it. We estimated how long it would take to circle all the numbers in order. Guesses were from 1 minute to 6 minutes. We put on a timer and started to circle! It took the fastest student about 8.5 minutes, and some were still working at 13 minutes.

Groups of 4 students each with a different marker colour tried the task again. They anticipated it would take less time, but they were pretty surprised when they saw the pattern that emerged. Each person’s numbers were concentrated in a corner, which became visible when the different colours are used.

Groups finished in about 5 minutes this time. Students helped each other find their numbers, and they were able to look ahead and plan for the next number to circle while others took their turn.
We tried the challenge once more, now that the pattern was visible. Groups had the opportunity to strategize, to move furniture, move themselves, make a plan, and it sure worked!

Groups drew outlines on their search quadrant, they were speaking numbers out loud, helping to point out what comes next, and of course, as usually is the case, someone just decided to circle all their numbers NOT in order to be fast. This task allows all kinds of behaviours to be observed! It took most groups 2.5 minutes to complete the task this 3rd time.
We talked through all of the positive group work skills that were demonstrated, and hope to see all term.
First day of Grade 9
We started off Grade 9 with a fun challenge. We’ve done this for many years now, but this group seemed to be particularly good at solving the task and being resilient when confronted with challenges.
The challenges are Sky Scraper Puzzles. They are kind of like sudoku puzzles. You need a building that is 4 floors tall, 3 floors tall, 2 floors tall and 1 floor tall in each row and column. Also, there are numbers on the side of the grids. These numbers indicate the number of buildings that are visible from that location.

There are 4×4 grids which are generally quite solvable once you find a good strategy, and there are 5×5 grids which in the past have been very challenging. This year most groups succeeded. Some solved 3 of the 5×5 puzzles!

We got to experience frustration, elation, teamwork, strategizing, starting over after making mistakes. There were many conversations about how looking at a task from different directions is so important, and trusting your group members to catch some mistakes, and trusting yourself enough to engage in the task with effort.
After we worked through these challenges we celebrated our very first Vennsday! (We celebrate on Wednesdays)

Our Venn for the day was one circle that were divisible by 3, another divisible by 5 and the third was greater than 100. Teams worked together to put as many numbers as they could in the different sections. We had some good chats about the logic used to approach the task, and also some of the characteristics of each section on the diagram, like if something is divisible by 5 and by 3 it will be divisible by 15. We noticed that there is a limitation to how many values are in that particular section. The centre section could actually have many more values, since numbers bigger than 100 keep going forever. We also got to talk about how 100 is not greater than 100, it is equal to 100. Hopefully this type of task will also help when we explore inequalities later on.
We enjoy these weekly moments to talk about numeracy, and to keep bringing up different number sets and their properties, and densities.

Grade 9s did such a good job cleaning up, that we had time for a game of “buzz” like we played in grade 10 (the previous post). Since this class is in French, there are added challenges with being able to say numbers larger than 60. It’s a good thing to practice!