Painted Cube Revisited
I was invited to run through the painted cube problem for another class of grade 10s. With each iteration of these rich tasks it’s neat ro see the different connections that can be made.
To refresh: the task is to imagine that a 3×3 cube is dunked in paint, then dried, then disassembled. We need to categorize each little sub cube by the number of faces that have paint.

Once groups have managed a 3x3x3 cube, they are asked to try a 4x4x4 or a 5x5x5 or a 6x6x6 or a 10x10x10 or the general case of (x)(x)(x).

Students come up with all the equations to model the relationships, then are asked to graph the relationships.
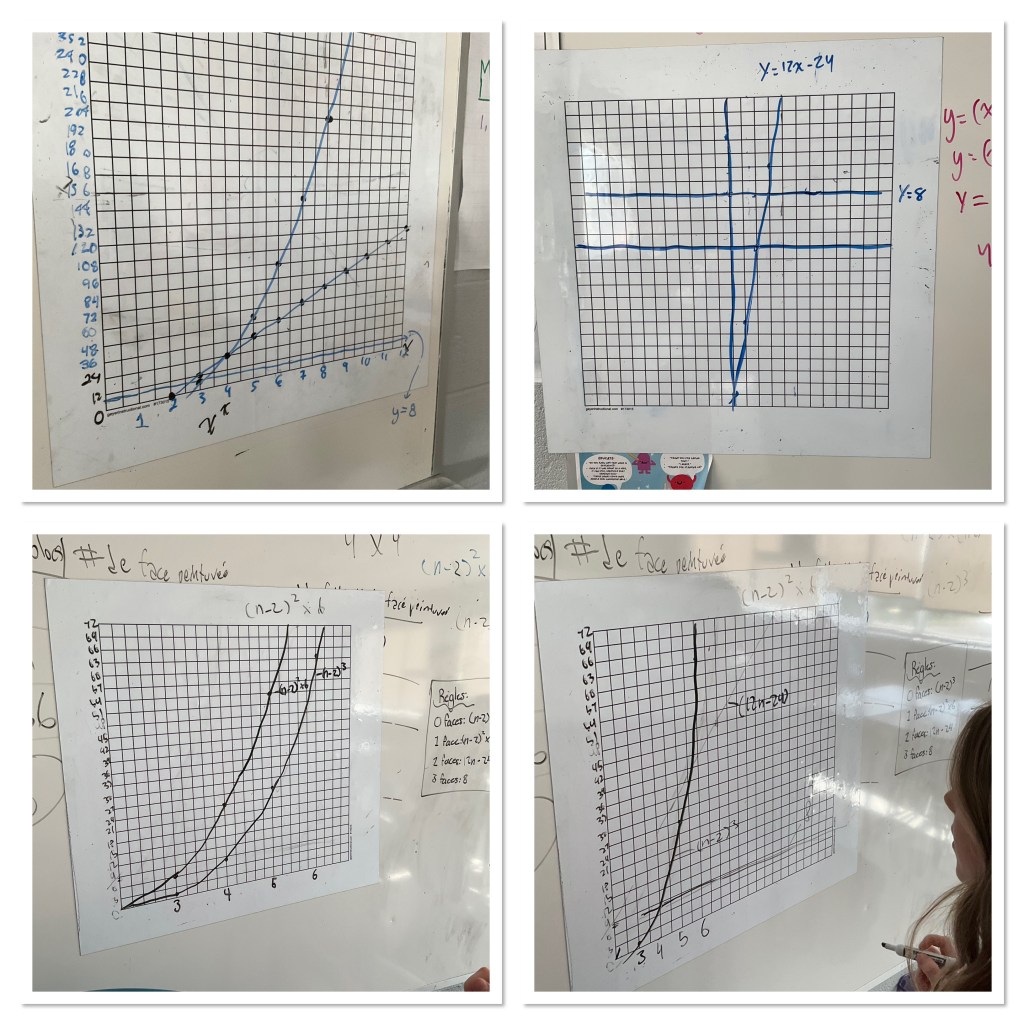
What was interesting with this group was that they wanted to find the intersection of the curves algebraically. We got into some good discussions about how to multiply a binomial by a trinomial, and also about how to solve by substitution.

we discovered later that the best way to approach this particular intersection in grade 10 is with u substitution, since we can’t really deal with factor theorem or solving cubics.
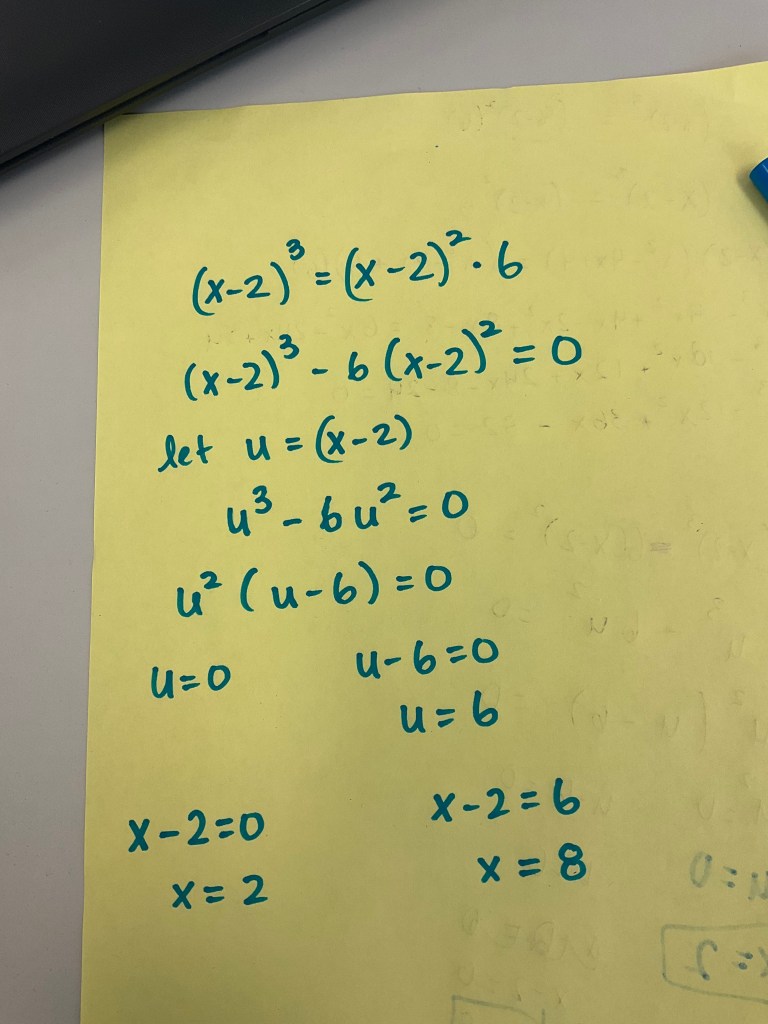
The other intersections are all really good to do for grade 10s. It’s good practice for solving linear systems by substitution, or solving systems by factoring.
This task gets richer with each iteration! Looking forward to seeing what we notice the next time through.
Painted Cube
Today my grade 10s invited the grade 10 class from across the hall to come over to do math together. We worked in co-mingled random groups of 3-4 students to tackle the problem of the painted cube.

The question is: imagine a cube, like a Rubik’s cube, 3x3x3. The cube is dunked in a bucket of paint. When dried off, the cube is taken apart to reveal the little cubes that make it up. How many of those little cubes have no paint? How many have 1 face painted? How many have 2 faces painted, and how many have 3 faces painted? Do any have all faces painted?
Students worked together to understand and represent the problem, and to work through their answers. There were excellent drawings and tables created.
we pushed the thinking to a 4x4x4 and a 5x5x5 situation. Some wanted to do a 100x100x100 cube! Many decided to create a general rule or equation for each number of painted faces.

To help model their thinking, some groups used the linking cubes we have in our room. The concrete tools really help us visualize 3 dimensional problems.

After pushing groups to consider a general formula, we asked them to graph them, and continue their model into the hypothetical range of negative sided cubes. The whole cube scenario falls apart, but the models keep going.
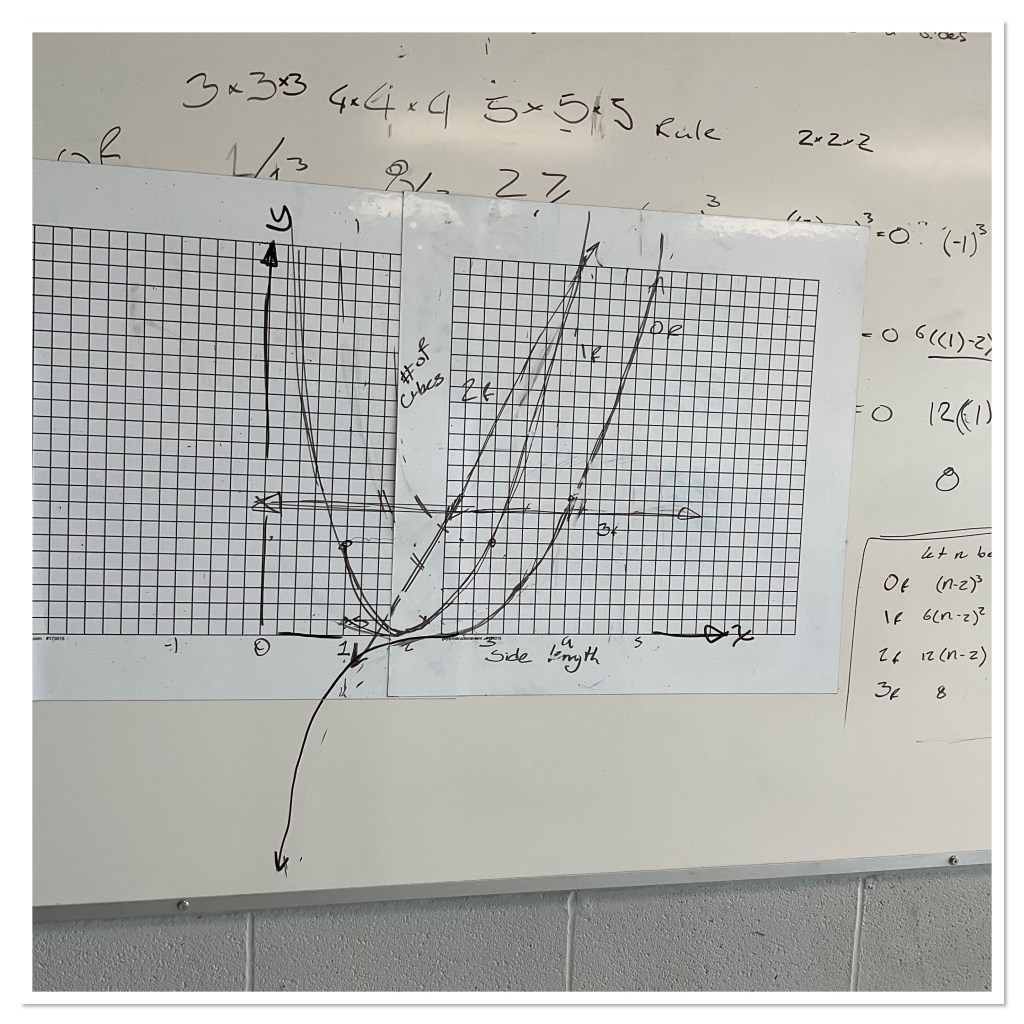
some students were interested in restricting the domain, to tell the region where the model works. We need whole number values for x, and they have to be bigger than 2.
It was fun to see the room so full of active math. Groups worked well together. Some students were concerned about having never solved a problem like this before, but took risks, and tried things, and realized by the end that the thinking is the goal. The thinking about the problem, and modelling the problem is far more valuable than knowing the number of painty sides on a cube. The ability to think, communicate, and represent the question in multiple ways is the skill which will be quite useful in future math classes.
hopefully we can have another problem solving day with our neighbouring class in the near future.
Completing the Square
Today was completing the square day in several grade 10 classes. We used algebra tiles to work on understanding how to complete the square to write a quadratic in vertex form.
here we have x^2 -6x+2. We arrange the tiles to make a square. It’s not complete though. We need 7 more red tiles to complete the square. We can only add zero pairs, so we will put the red tiles in the square to complete it, and then have the blue tiles alongside the square.

in vertex form we have (x-3)^2-7

when we have a leading coefficient we are no longer completing the square, we are completing the squares (plural). Each x^2 tile is the base for an identical square.

we will be working on vertex form and graphing over the next while.
algebra tiles are a great low-tech solution for teaching engaging lessons while faced with a network outage. It appears we’re working without internet, online class resources, and very limited access to printing for the foreseeable future. Glad to have the consistency of tiles and graph paper, and lots of whiteboard markers. We will still be able to make great use of our time.
Perpendicular Bisector
We worked on perpendicular bisectors in grade 10 math. The challenge was to locate the points A(-3,0) and B(5,0), and then to find as many points as possible that were an equal distance to A and B.

We had a discussion about how we knew that these points were all the same distance to A and B, by using the distance formula/pythagorean theorem.
We did the same task but with points A(0,3) and B(0,7). We noticed that the line of equal distanced points is perpendicular to the initial segment, and went through the midpoint.

The next challenge was to use the points A(1,2) and B(3,6)

we know that the slope of the segment is 2/1 so the slope of the line we draw is -1/2. We know the line goes through the midpoint, and we’re great at calculating midpoints!
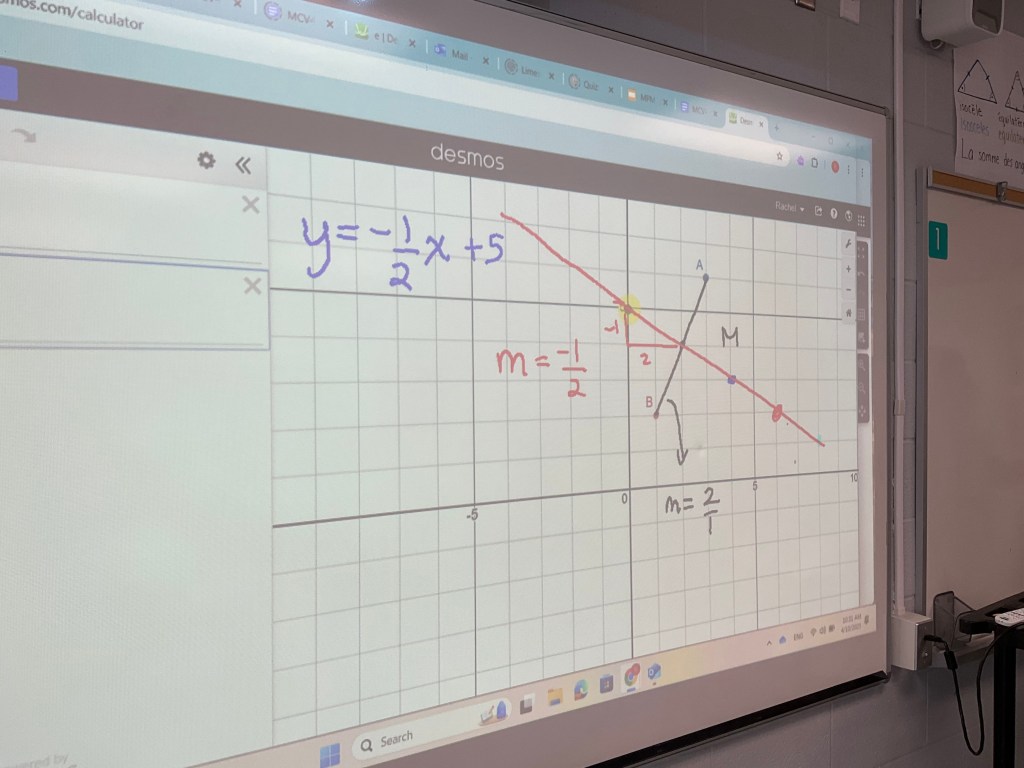
Our final step is to make the equation of the line, which we learned is called the perpendicular bisector (médiatrice). We’re able to use our skills from lap 1 to help us a lot with these questions.
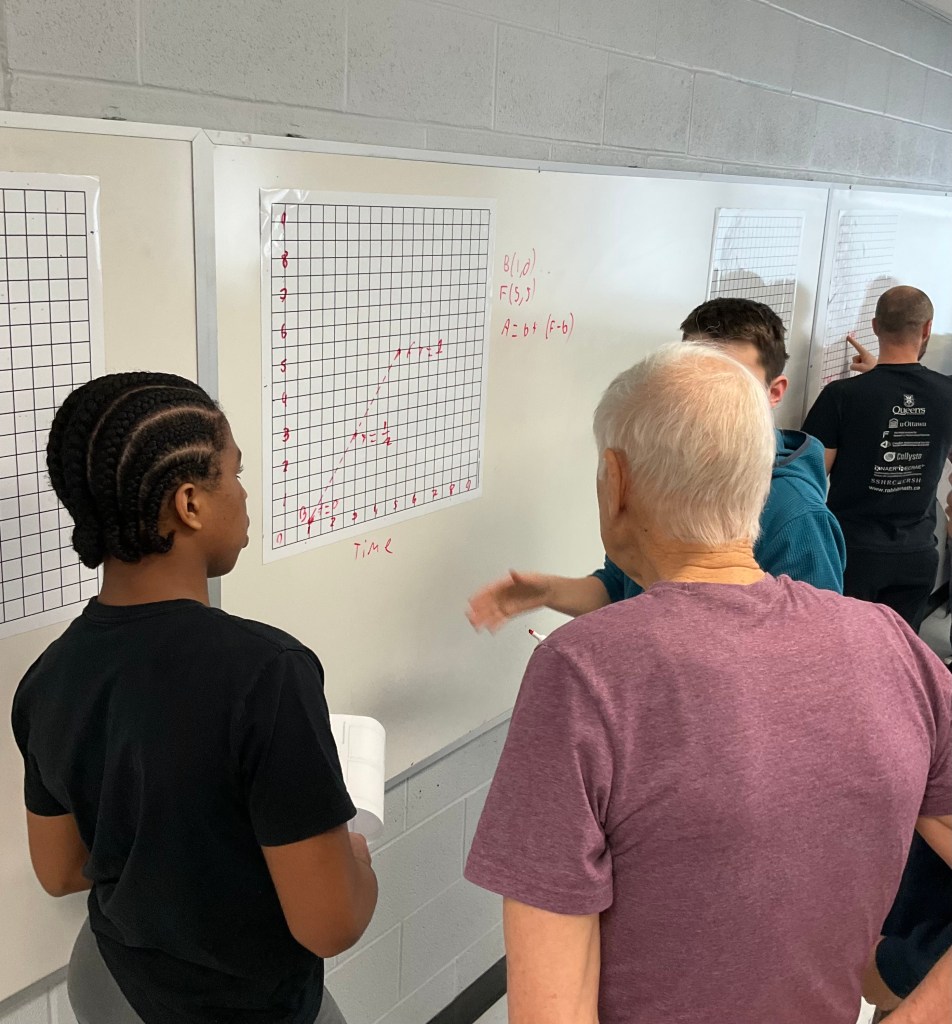
Special Guests In Grade 10
Today we had the pleasure of welcoming Dr. Peter Taylor and several graduate students from Queen’s University, and RabbitMath to come and do some problems with us.
In grade 9 and 10 the problem we did was a neat one which showed a way of representing a line using a parameter. Students drew the line segment between the points (1,0) and (5,5).

the journey from point to point took 1 minute. The next task was to determine where the halfway point would be? Where you’d be after 0.5 minutes, t=1/2, and the also where you’d be when t=1/4, or t=4/5.
There were great discussions happening in the groups, and students were pushed to justify their conclusions and explain their thinking.
Next we brought in a parameter t, and we were able to express the point on the line for any value of t with the following equation.
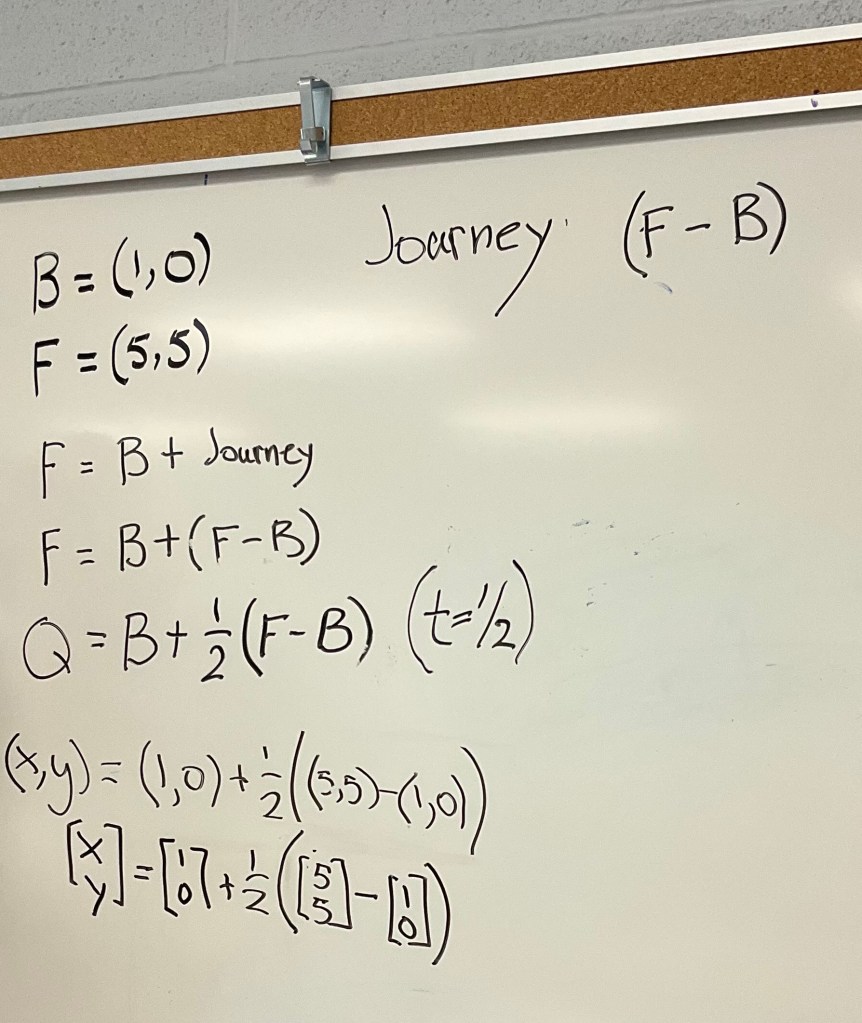
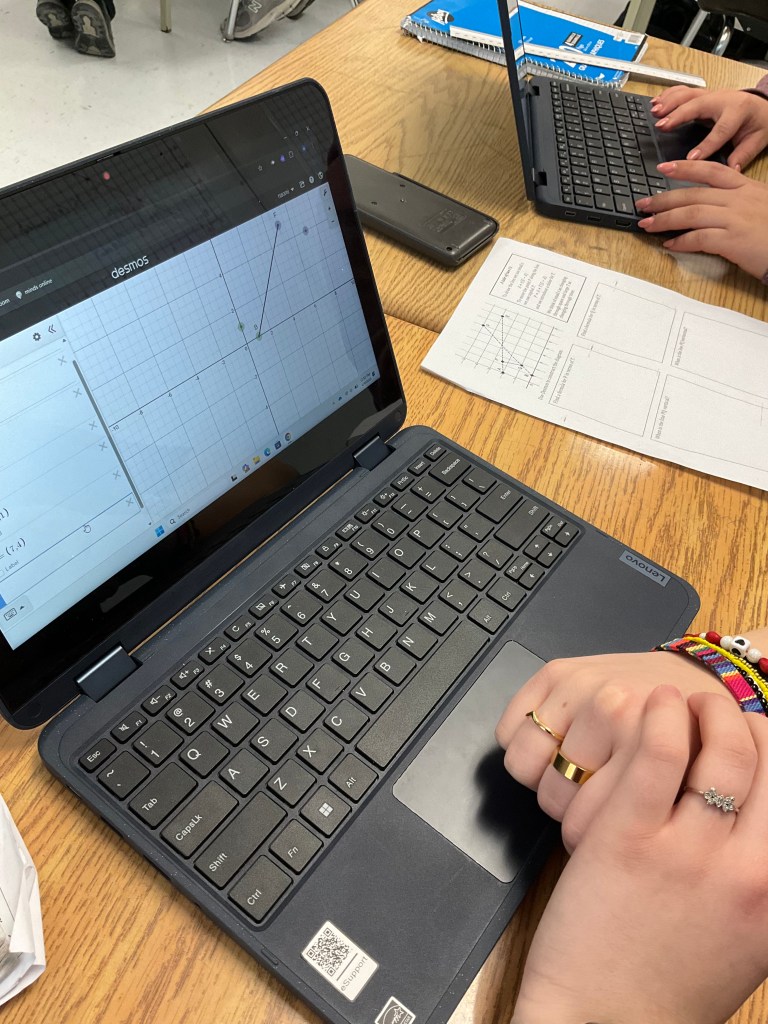
We turned to desmos and built a model
we used B=(1,0) and F=(5,5)
then we defined the line to be B+t(F-B) where t is a parameter

then we put a point on the line that could be animated with a slider. Q=B+T(F-B) where the capital T is controlled with a slider between 0 and 1.
We made another line as well, and added a slider dot on that one too.

The final part was to make a line that joined the sliding dots together. We were exploring when that new line segment was vertical and when it was horizontal.
Here is the desmos result. It was pretty cool!
Students and teachers learned a great deal from this experience, and it was fun to do something totally different. We are thankful to our visitors for bringing good questions to share with us, and the support as we explored the math.
Solving Trig Problems

We’ve been having fun solving trig problems today. We can now recognize when to use sine cosine and tangent to solve for unknown sides or angles.

We’re working up at the whiteboards in our small groups, helping each other, sharing ideas, and checking our answers. It’s been a great 2 days of learning!
Patterns, Equations and Graphs
Today I was invited to work with a class on patterning, and equations and graphing.

We built and extended the pattern using square tiles. We noticed that we added 2 new tiles each time, and we can see that we always add the new tiles in the same place. We can also see that figure 0 would have 1 tree. Figure 0 is the constant. It’s always there. We thought about how many trees would be in figure 10, or figure 100. We could make a table, and we could add 2 and add 2 and add 2 until we get to figure 100, but that is tedious, so we can think about how many groups of 2 you added. To get to figure 100 we add 2 100 times to the 1 that we started with. To get to figure x, we add 2 x times to the 1 that we started with. The equation, or pattern rule, is y=2x+1
We had some fun building our own patterns and sharing the rules.

We saw some neat patterns:

this one is y=2x+1

the figure 2 is a bit different here, but the pattern was cool, going up by 6 each time, we’d need a negative constant.

i was impressed at how many groups made negative constants without any issue. I likes how we have different colours for positives and negatives in these representations.

this was a neat pattern that was fun to unpack. We looked at how it grew and noticed that it was not linear because we added different amounts each time. We saw that we could split the figure into a square and 1 extra tile. The constant is 1 since figure 0 is 1. We determined the equation was y=x^2+1.


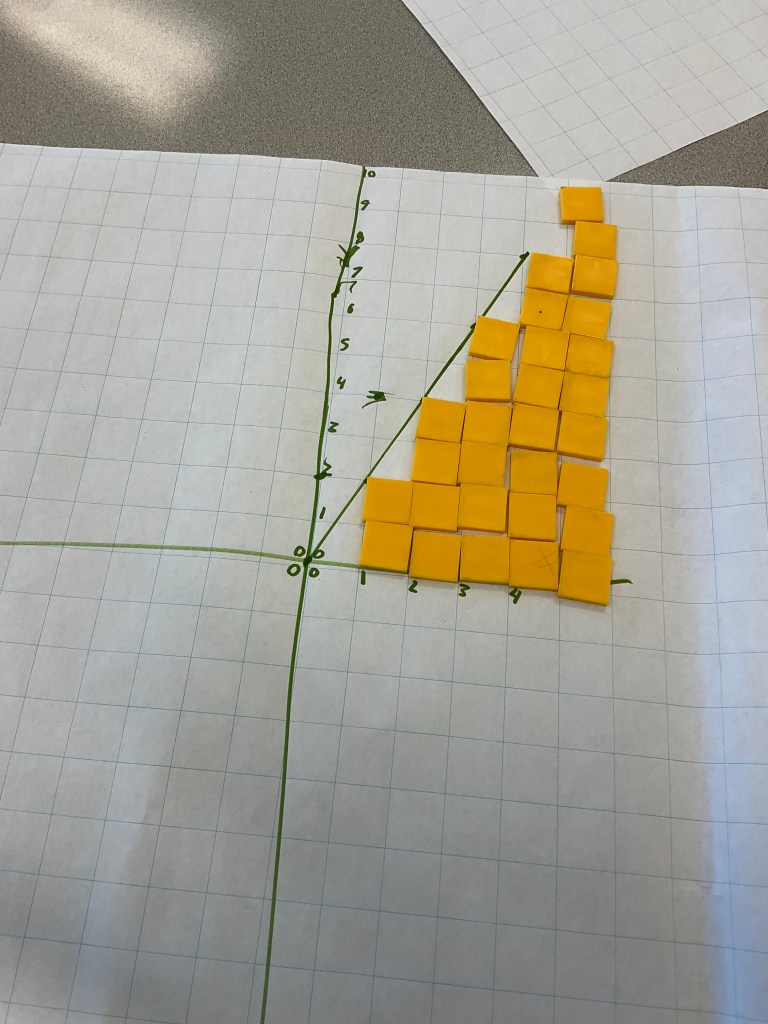

Groups had 2 pattern rules to explore and graph on the same axes with different colours.
here are the results:

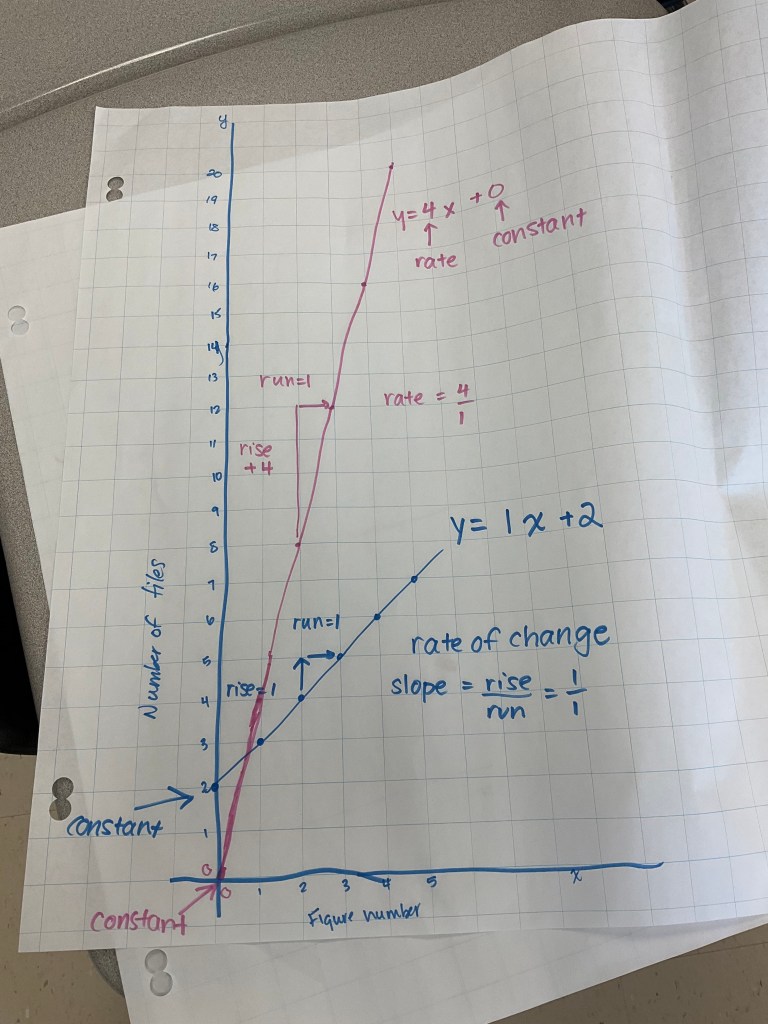
these two lines are parallel, they have the same slope, and different constants, and they will never intersect.

Many thanks to the class for inviting me to come share some activities. I hope to be back again to try something similar with quadratic patterns!
Introduction to Primary Trig Ratios
Today in grade 10 we looked at right angle trigonometry. The initial prompt was to use a ruler and protractor and draw a right angle triangle that has an angle of 30 degrees.

The next prompt was to measure each side, and record the values in the chart on the wall. The headings were “small side” “middle side” and “long side”.

Next I used my magical skills to tell everyone which triangles were perfectly drawn and measured.
My students know I’m not magic, so they were trying to figure out the trick or pattern I was using.
Pretty quickly they concluded that the small side was half the length of the longest side.
This is how we started the discussion about trig ratios. I showed them a trig table book from 1965 that was used at KCVI before the age of calculators.
We explored how we can use calculators to solve for missing sides and angles. It’ll take more practice, but we’re well on our way to solving right triangles now!
Fraction Fun

today we worked on fractions in MAT1L. Our focus was on using relational rods (Cuisinaire rods) to represent and compare fractions. Before we got started we reviewed the vocabulary of numerator and denominator, and practiced saying the words out loud together. We talked about if the numerator and denominator are the same how that equals 1. It was great to see some prior knowledge bubbling up.
We used a concept circle with 1 being represented by a rod of length 12. We built equivalent fractions to the central “1” using different blocks. Here it shows that it takes 6 red blocks to build the 1, so we know that each red blocks is 1/6th.

We worked hard to represent each fraction
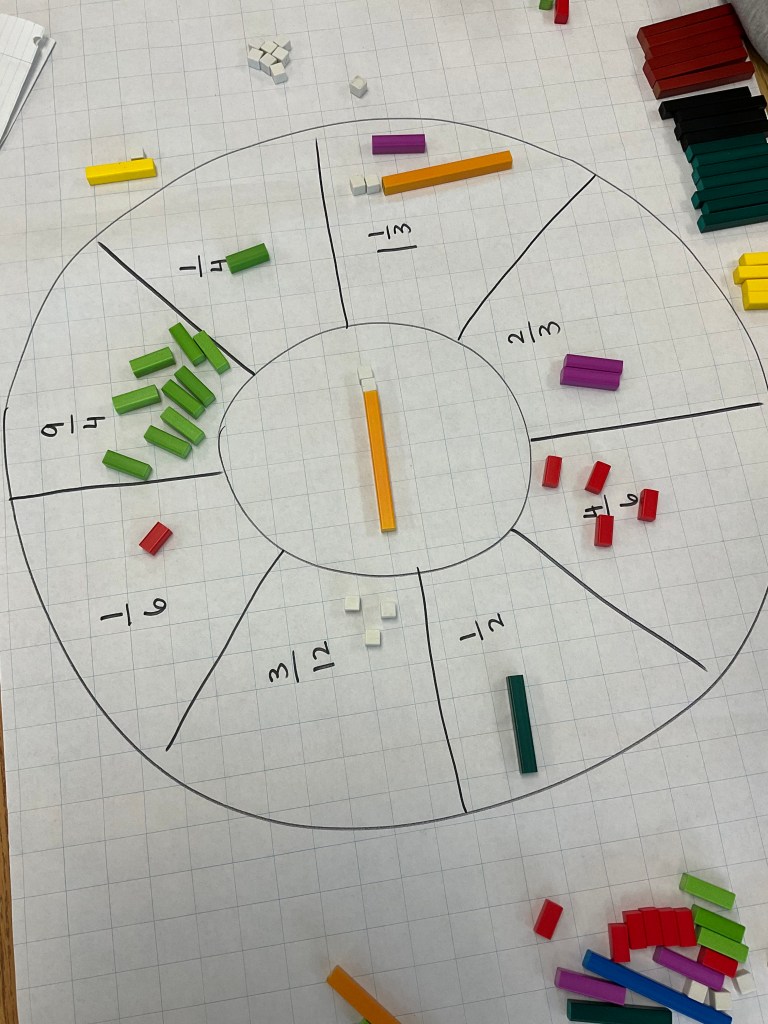
Next we looked for equivalent fractions by comparing lengths. We noticed that our magical multiplier is the same as the ratio between the blocks. Each 1/4 is split into 3, and each smaller portion is 1/12. It takes 3/12 to make 1/4.
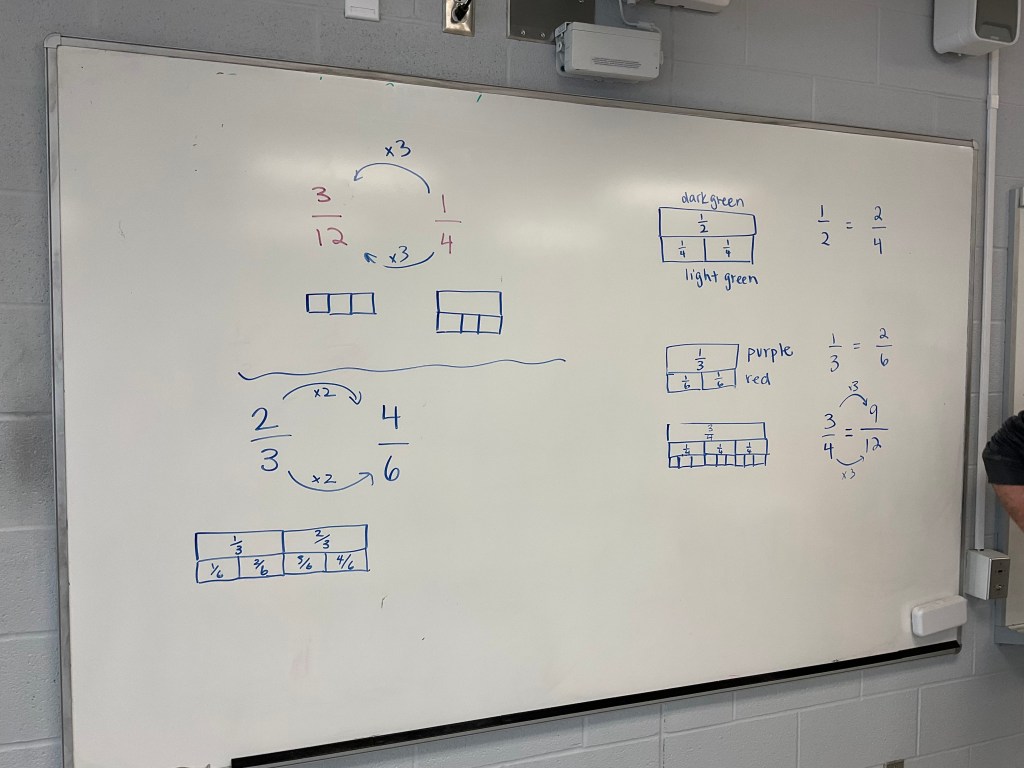
we made some equivalents: 9/12=3/4. The blue rod is 3/4.

here’s another equivalence: 6/12=2/4=3/6 shown with the red, green and white.
we also noticed we could build rods of the same length. We have the blue which we already determined was 3/4 or 9/12 and to that we add a white which is 1/12, we know that 9/12+1/12=5/12+5/12. Each yellow is 5/12.

we had some success making fractions fun today. There were some thumbs up at the end of the class!
Algebra tiles for equation solving
Today I was invited to work with a grade 9 class to introduce equation solving with algebra tiles. We looked at what the tiles were, reviewed some of their understanding about combining like terms and making zero pairs, and then set off to solve.
We started with simple equations like x+3=-7 where students could likely solve by inspection, but we were introducing how to build the expressions with tiles and use the tiles and zero pairs to solve.
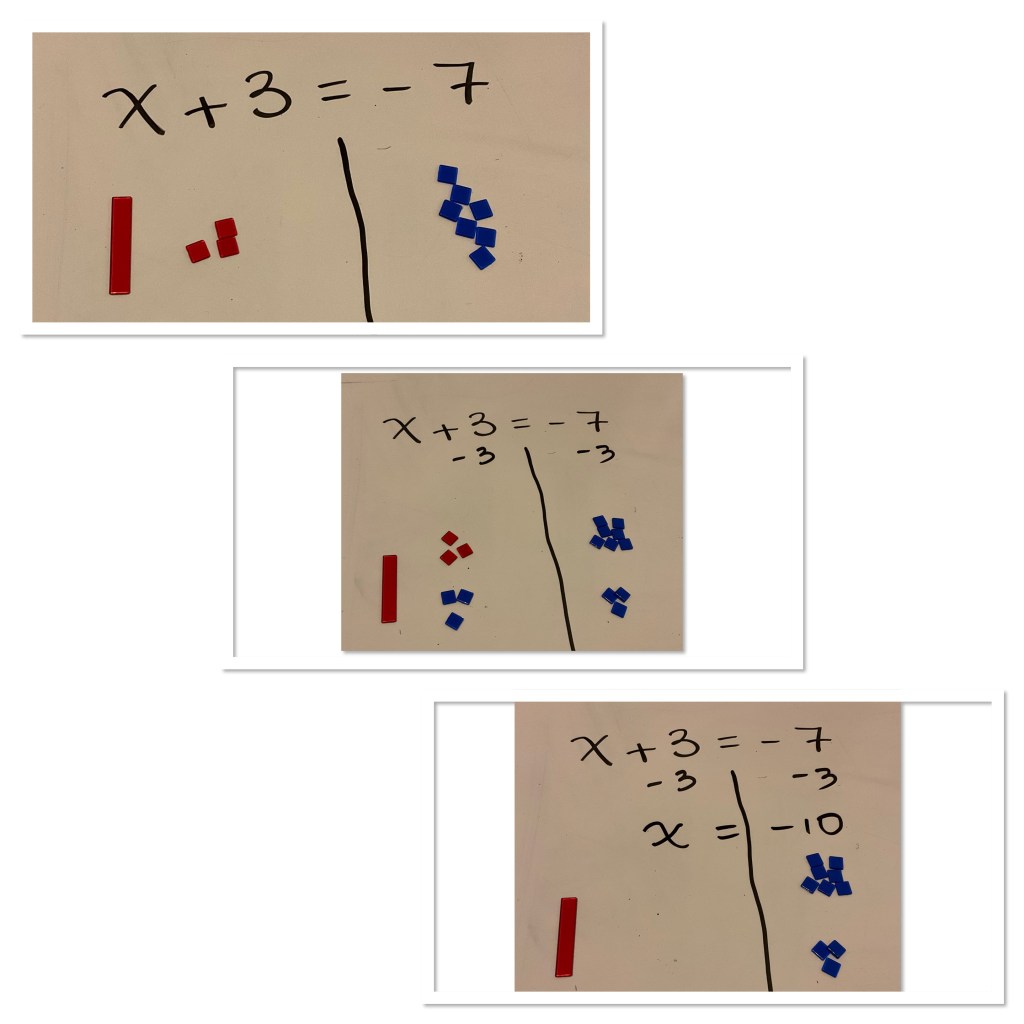
We worked through a sequence of problems adding more complexity as we went. After doing several similar questions with x on one side, we made a coefficient for x, e.g, 2x+5=1

Then after a few of those types of problems we introduced a question that would result in a fractional result e.g. 3x+1=5

The final step caused some discussion. We can split the x term into 3 groups, but we can’t split the 4 into 3 equal groups without cutting up a tile. Some students showed the answer as x=1 and 1/3, some said the answer is x=4/3 since it’s 4 tiles split into 3 groups. Pretty neat!
Next we did some questions with x on both sides like 2x+1=4x-3. We needed a strategy of using zero pairs to get x on one side only to start with, and then we used zero pairs to get the constant terms on the opposite side. Finally we made enough groups for each x to have a group.

finally we levelled up to doing problems with distributive property and x on both sides. The class had recently worked with distributive property with algebra tiles so this was a bit of a challenge, but not something completely new to them.
We did questions like 2(-x+3)=3(2x-1)

By doing questions in this sequence students became confident with what becomes the final steps of solving, so in each subsequent level of challenge they will review those final steps over and over again building up their understanding and confidence.
It was a really interesting visit with the class. The tiles unlocked understanding for several students who had not always participated with confidence, and they told me that math class was great that day, and that they were feeling good about their skills for a change. I was glad to see a strong reception by some. Other students seemed a bit more hesitant to buy in and try.