Distributive Property
Today several grade 9 classes were working on the distributive property and how that applies to multiplying monomials by binomials.
We started with representing multiplication with tiles. Here is an example of (2)(3), a 2×3 rectangle involving 6 unit tiles. The area is the product and the dimensions are the factors.
Next we tried 3x, which can be seen as 3 groups of x (below)
or we can make a rectangle with one dimension as 3 and the other as x.
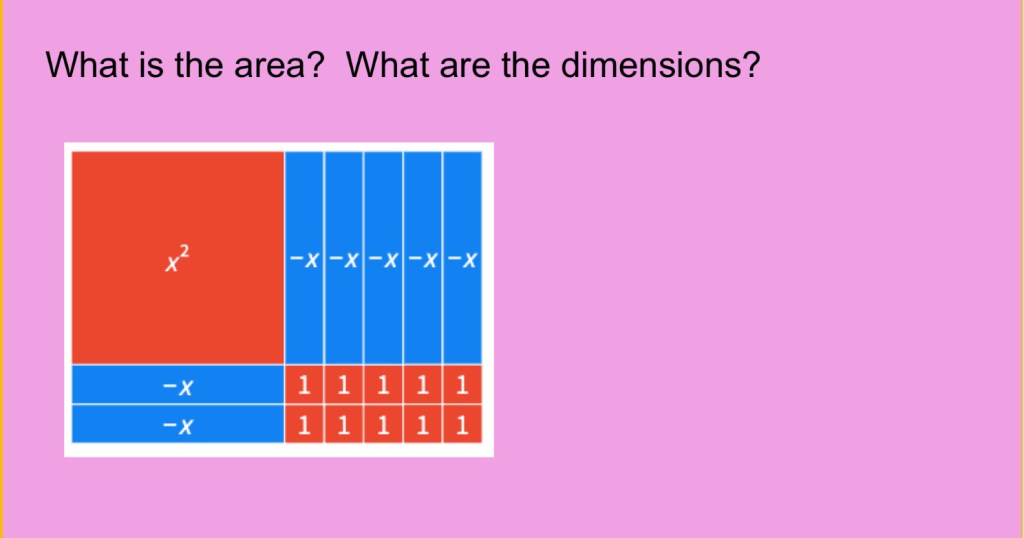
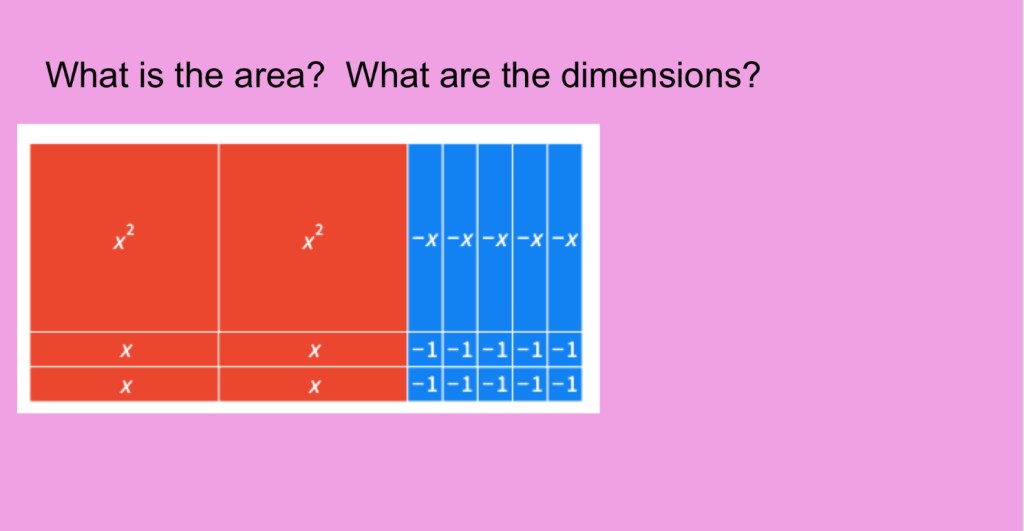
The next interesting thing to try is to make as many rectangles as possible for 12x.
we can write these as products. (1)(12x) is the long thin rectangle (top left), then (2)(6x) which is bottom left, then (4)(3x) bottom right and (6)(2x) top right. There could also be (3)(4x) and (12)(x) which are not shown.
Here is another challenge. There are different ways of writing 2(3x+1)
many students see and understand this as 2 groups of (3x+1) which is great. We know there will be 2 groups of 3x, and 2 groups of 1. We can also show this as a rectangle with dimensions of (2) and (3x+1).
The rectangle idea is important when we get to a situation of x(x+2). We struggle to understand x groups of x+2, but we can create a rectangle with dimensions of (x) and (x+2).
We next cut up a puzzle and tried to match the sides that have equivalent expressions
We got them sorted out! It took a while, but our teams worked hard and mastered the challenge.
For more puzzles like this check out monclasseurdemaths
Introduction to Spreadsheets
We were working with spreadsheets today in grade 9 math. Students measured their foot size and their height and we put the information into a shared spreadsheet.
We looked at how google sheets can make a scatter plot, and add a trend line with an equation and R-squared value. We also used our graph to make some predictions.
We also explored how we can use coding to calculate the maximum and minimum values in a column of data. We also used coding to calculate the median, mode, and mean, and used the max and min to calculate the range.
Introducing Algebra
Today we started algebra in several grade 9 classes. We started by using algebra tiles to make some pictures.
Next we eliminated all the zero pairs and simplified the expressions into polynomials.
We talked about the vocabulary of algebra, introducing the words “like terms”, “coefficient”, “constant”, “variable”, “exponent”, “trinomial”, “binomial”, “monomial”, “polynomial” and then started creating some polynomials, then adding polynomials together and combining like terms, and simplifying.
Later we had challenge questions to create the following:
(Binomial)+(binomial)=(trinomial)
(trinomial)+(trinomial)=(monomial)
With tiles the algebra is more tangible and less abstract.
Distance and Midpoint
We were up at the walls working on determining length of a segment, and midpoint of a segment today.
The sequence I used is as follows:
Plot the points (0,2) and (8,2). Determine the length of the line segment. (This is pretty simple to do by counting).
Plot the points (-1,-2) and (-1,4) and determine the length of the line segment. I asked students to think of how they could calculate the distance with operations. They decided that subtracting works 4-(-2)=6.
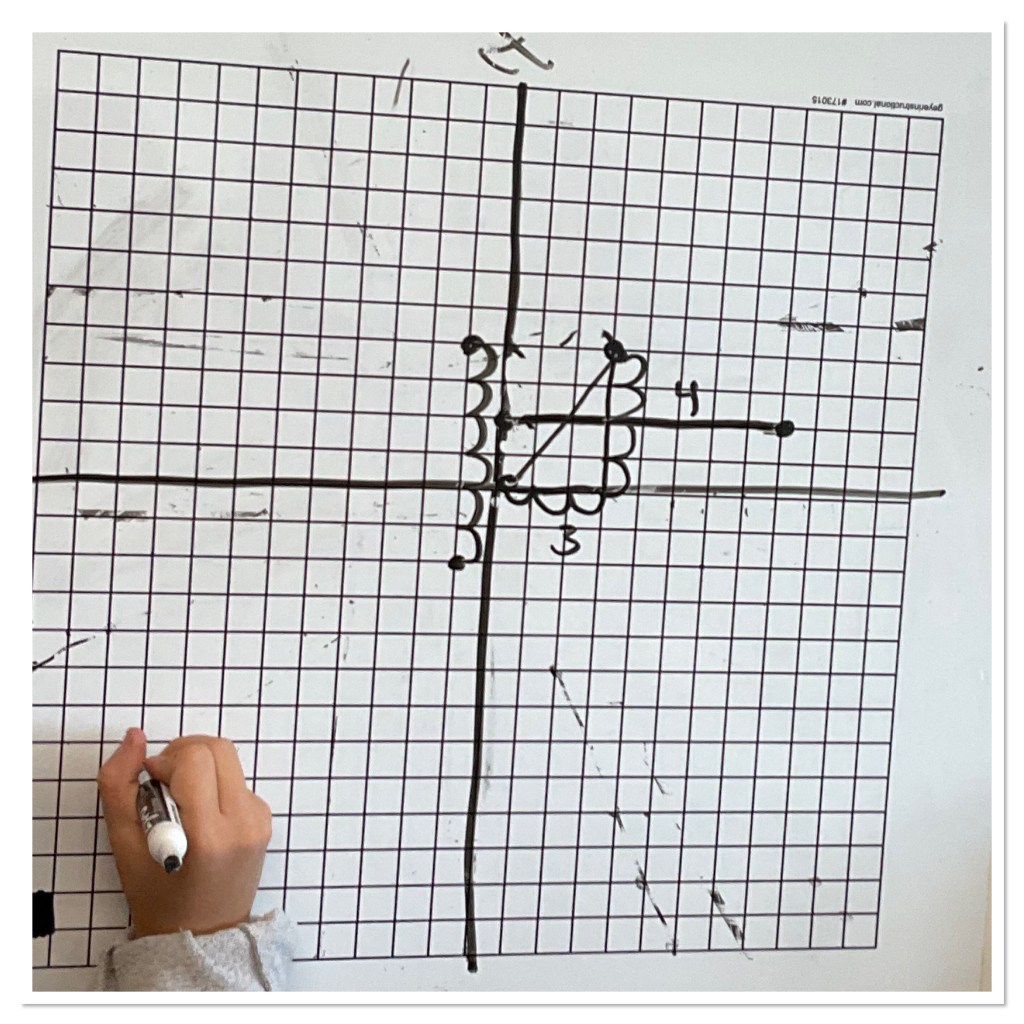
The next challenge was to find the length of the segment between (0,0) and (3,4). There was a bit of a struggle, until some students started to draw a right triangle to help.
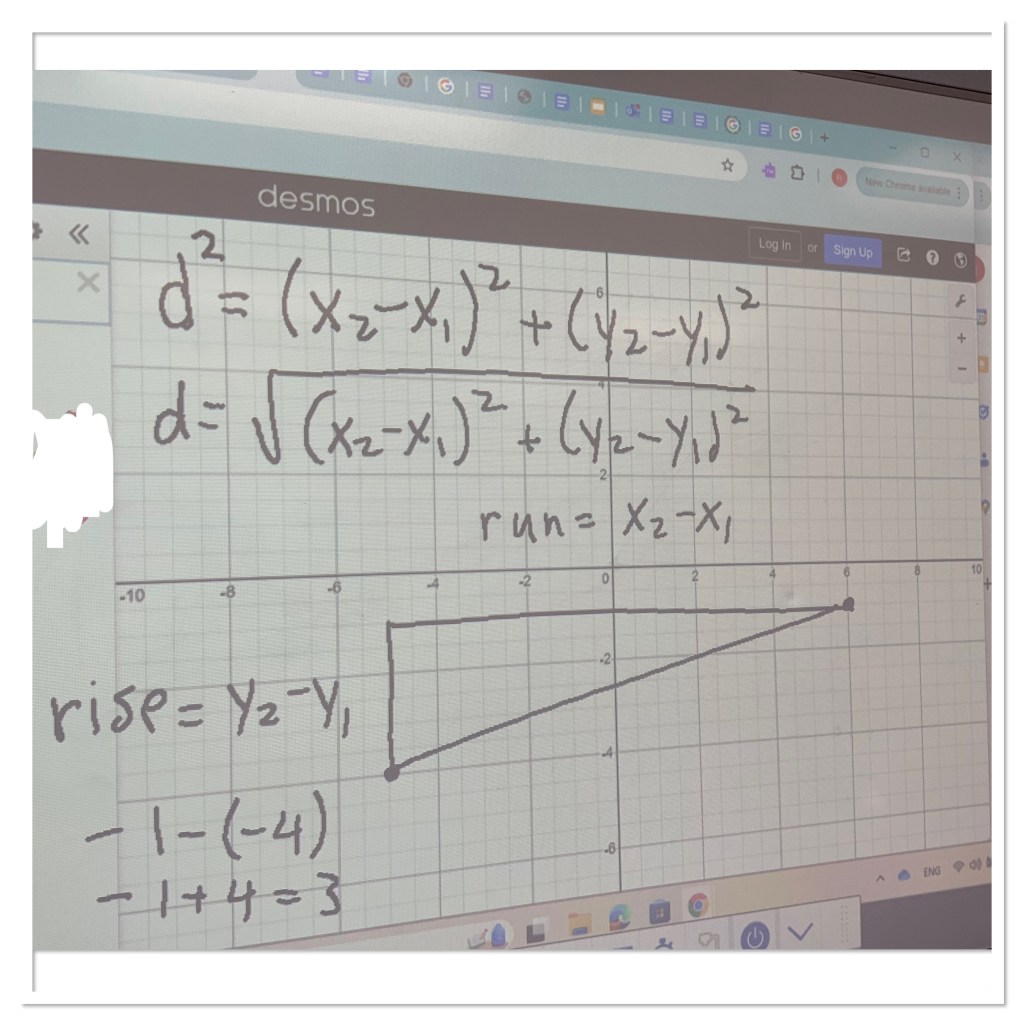
I asked some groups to try to find the distance between any two points (x1,y1) and (x2,y2). It was neat to see students use their idea of rise and run to create an equation.
We consolidated as a group and derived the distance formula that they will be given.
The sequence for determining the midpoint was similar. We looked at the midpoint of a horizontal segment, a vertical segment that had end points in different quadrants, and then for a segment that is on a slant.
It was interesting to see the connections that students made to their prior learning. Some were discussing the fact that a horizontal segment has a y value that is always the same, and a vertical segment has an x value that is always the same. Other students used the idea of finding the middle by taking the average. Pretty soon we were all taking the average of the x values, the average of the y values, and putting that in (x,y) form as the midpoint.
Introduction to Algebra
I had the pleasure of being in a grade 9 class as they started their algebra lessons. There was a “which one doesn’t belong” which helped to introduce the need for some vocabulary to discuss algebra. Terms, and coefficients, and constants, and like terms, and exponents were all discussed, and students had some neat ideas about what a variable is: something that holds value, but can change. One student suggested that -3 is the only number of the 4 that we actually know.
Following this, algebra tiles were introduced, and students built pictures.
After the pictures were built, they wrote expressions for their pictures, then simplified the polynomials into their simplest form. New vocabulary was introduced to talk about monomials, binomials and trinomials.
A concept that is sometimes intimidating for students can be much more approachable when starting in this gentle way.
Factoring and Expanding with Tiles
Today I had the pleasure of working with a grade 10 academic math class to help introduce factoring and expanding using algebra tiles.
To start with, students were working on recreating the rectangles provided and stating their areas and dimensions. Here is the sequence of questions we used.
We know the area is the insides, so that is x^2+8x+15, and the dimensions are (x+3) and (x+5). We know the long sides are x, and the short sides are 1, and we read the dimensions of length and width of the rectangle.
We looked at how negative times a negative is a positive, and that is why we need 10 red squares in the corner.
Here we looked at zero pairs, and how the +x and -x will cancel each other to make zero.
Students had to work on making rectangles from these given sets of tiles. The 2nd example allows us to talk about perfect squares. The 3rd and 4th require some zero pairs to make the rectangles work out.
These examples have a few different ways to make rectangles. This is because there is a common factor of 2. We could split each polynomial up into 2 equal rectangles as well.
Finally, we tried giving dimensions, then building the rectangles to determine the area.
From these questions, students are essentially factoring and expanding using tiles. In spiral 2 we will go back and attach more algebra to these skills, and explore some patterns that are visible with the tiles.
Cookie Towers
Grade 9s are working on data collection and representation. Today we gathered some single variable data by making cookie towers. The rules are: hold one cookie at a time and place it on the tower. Cookies are stacked one on top of the other. We want to create the tallest tower possible.
There were various strategies attempted. Our tallest tower was 16 cookies.
After each group had 12 attempts we calculated the mean, median, mode, and range. Then we learned how to represent data in a box and whisker plot.
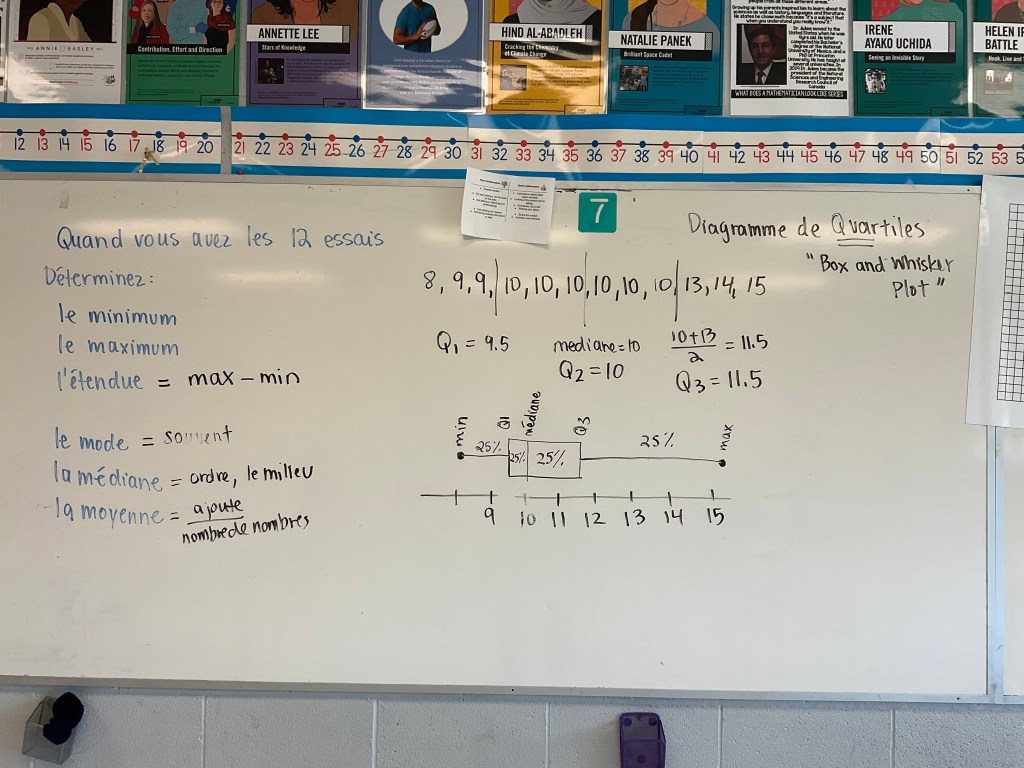
It was a fun way to end the week.
Parallèle: Même Pente!
In grade 10 my class has learned a call and answer….when I call out “parallèle” they will reply with “même pente” (same slope). We had not talked about this for a while, and were doing some review work in groups at the boards, and I flipped to this slide to end the class. The challenge is to find which figure number will have the same perimeter.
I was very impressed to see their way of working through the problem. This group made equations, then realized the slopes are the same, so they are parallel and will not intersect.
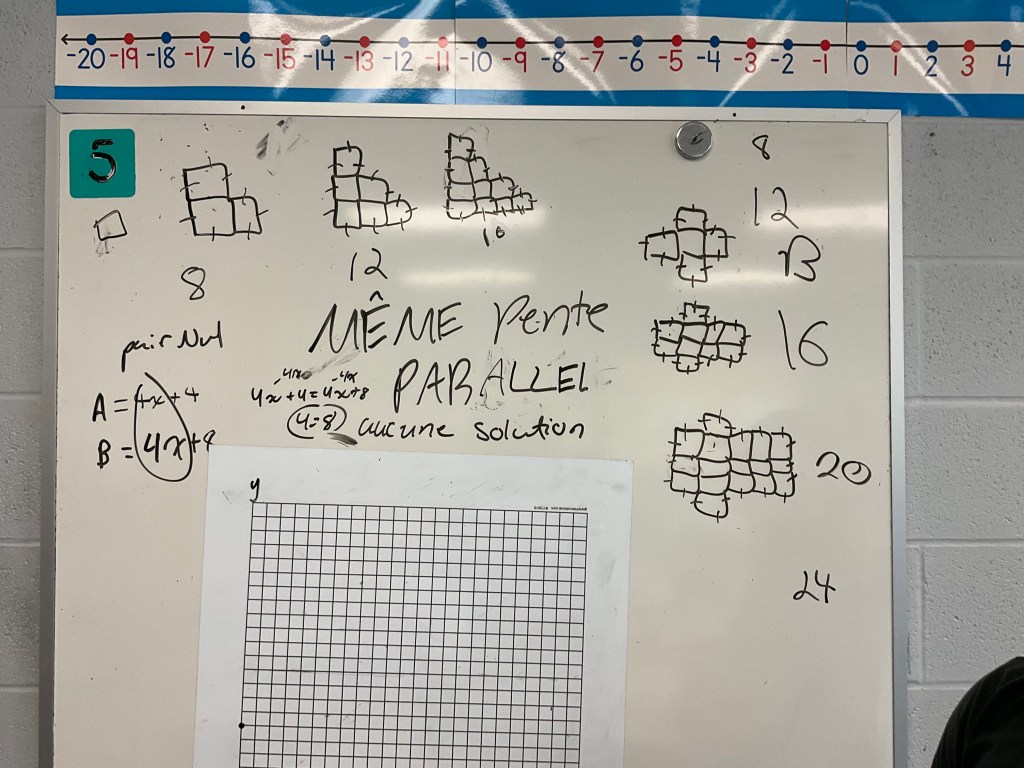
This group made a table of values for each pattern and noticed that the first differences are the same, so the slopes are the same, so they are parallel.
I am very pleased that even after not talking about it for a few days, that students have remembered that parallel lines have the same slope!
Progress in Grade 9
Since it’s Vennsday we did another numeracy task with Venn diagrams. This time we had one circle for even numbers, one for multiples of 3, and one for square numbers.
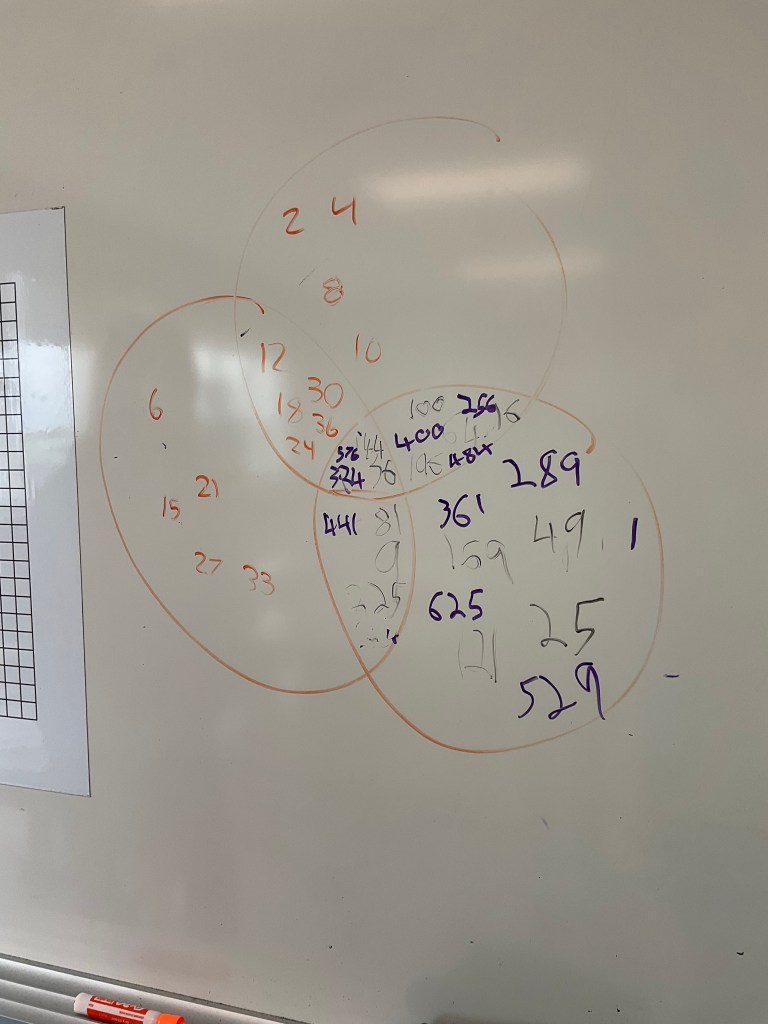
After this task, we did some work on composite perimeter and area. This is an area of challenge for the class this term.
We needed to use some logic to determine the missing side lengths, and then find the area of each rectangle, and then add them up.
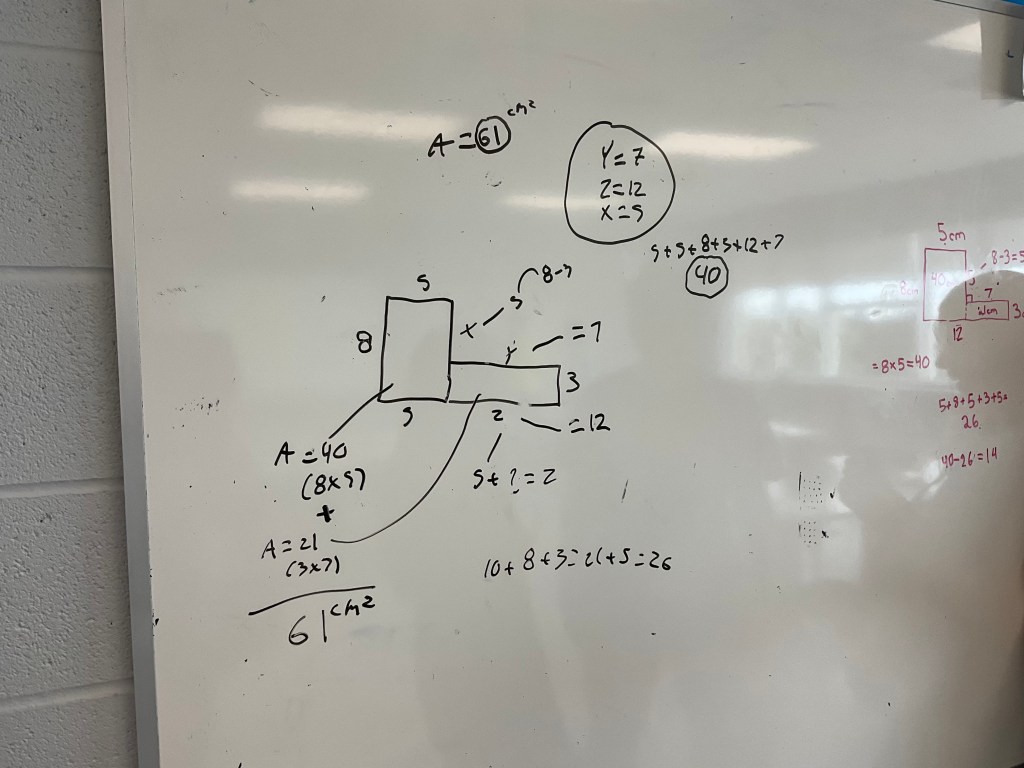
This question was a nice spicy one!
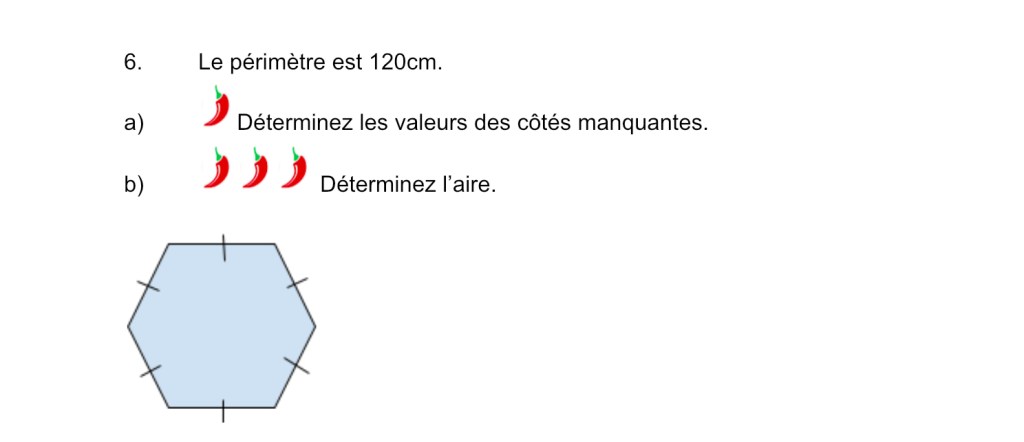
The side length is 20 for each side, but to determine the area we needed a bit of a hint.
A regular hexagon is made of 6 equilateral triangles, and the sides are all 20cm.
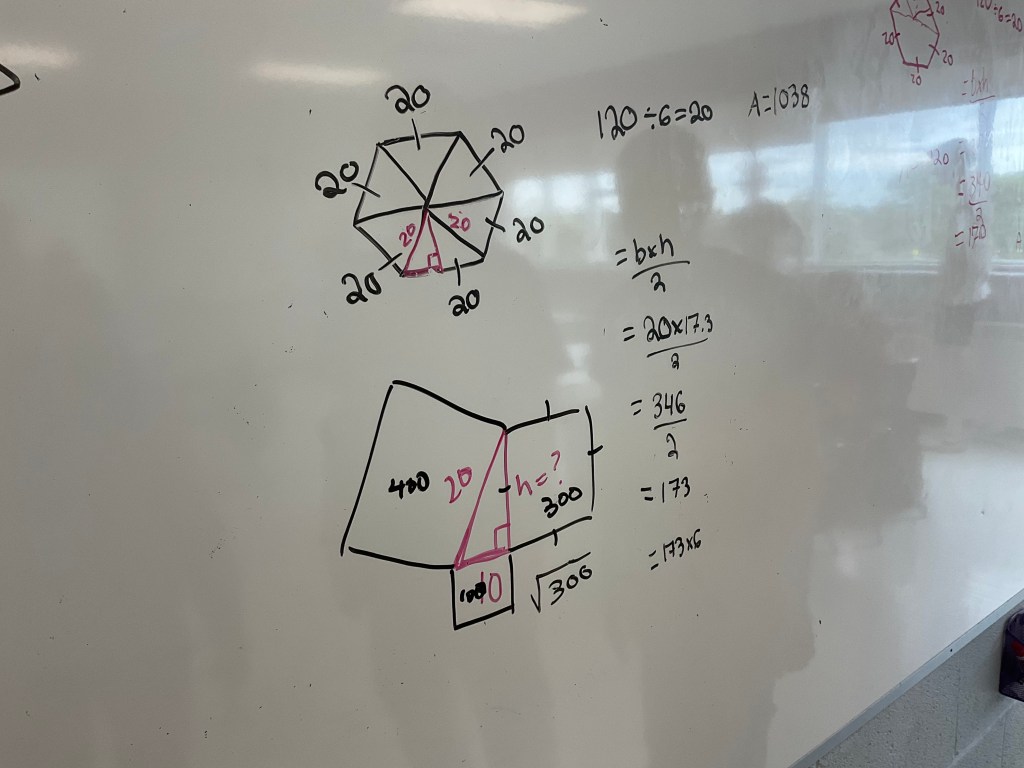
This is a nice diagnostic to see if students remember the pythagorean theorem. We’ll explore this more later, but we need to use it to find the height of each triangle.
We need to keep working on perimeter of composite shapes moving forward, but we are getting better with area.
Thinking Classroom
I had an opportunity to try a thinking classroom task with an MBF3C class. They have been working on quadratics and problem solving.
I introduced the rules of standing up at the boards, in random groups of 3, and each group has one marker, and the person who has the marker is not in charge of doing the thinking.
I gave the students a scenario of someone seeking riches through popcorn sales. They have talked with a business analyst who gave a profit equation. P=-60(x-4)^2+120, where P is profit and x is price of a bag of popcorn. I asked them if my friend’s plan of selling a bag for $6 is a smart plan.
Students worked in their groups, and many started with graphs. We needed a bit of prompting and some redirecting, but groups got there in the end, showing graphs that open down, with a vertex at (4,120).
Some groups decided to substitute a price of $6 into their equation to start.
making a negative profit is never a good idea!
Groups decided that the best price would be $4 per bag.
Ms. Bearse's Site 