Ms. Bearse's Site

We read the text and discussed what it means. We needed to look up a few words and draw a few pictures to make sense of the problem.

We strategized about how to solve the problem and made a good plan.

sometimes a lot of text makes it look like a scary question. Text gives us information, so more text is sometimes better!

We are working toward a test on Friday, and study notes are due on Friday as well.

In Grade 9 today we looked at how pyramids are related to prisms of the same base and height.

We filled the pyramids with water, and could dump them 3 times into the prism to fill them up. The volume of the pyramid is one third the volume of the prism with the same base and height.

We then worked on building pyramids with a volume of 300cm^3.

Some of us made an error that we can learn from. For some of us the pyramids ended up being shorter than we planned. We measured the pyramid height as the slant height of the pyramid (the height of the triangular face).

We can see that there is a right angle triangle hidden in this pyramid. Half of the base of the pyramid (pink), the pyramid height(black), and the slant height (orange) form the triangle.

So our first step is to choose good prism dimensions (there are many combinations that work. The base must be square, and the product of all dimensions must be 900cm^3).

Using the 10x10x9 case, we can calculate the height of each triangular face that we need to arrive at the correct pyramid height.

We looked at how this works with an example of a cone as well.

In order to find the volume of a cone, if given the slant height, we need to use the pythagorean theorem to calculate the height of the cone first, and then we can calculate the volume of the cone after.

Grade 9s had a look at some model portfolio responses and colour coded the sentences that they felt were evidence, reflection, and summary statements.

While they worked they brainstormed ideas for improving the writing samples, and decided on the “teacher comments” they’d write.

After that, students had a look at their own portfolios, to see how they could work on improving their own writing based on the feedback they’ve received. For the first submission portfolios can be bumped up after they’ve been marked.

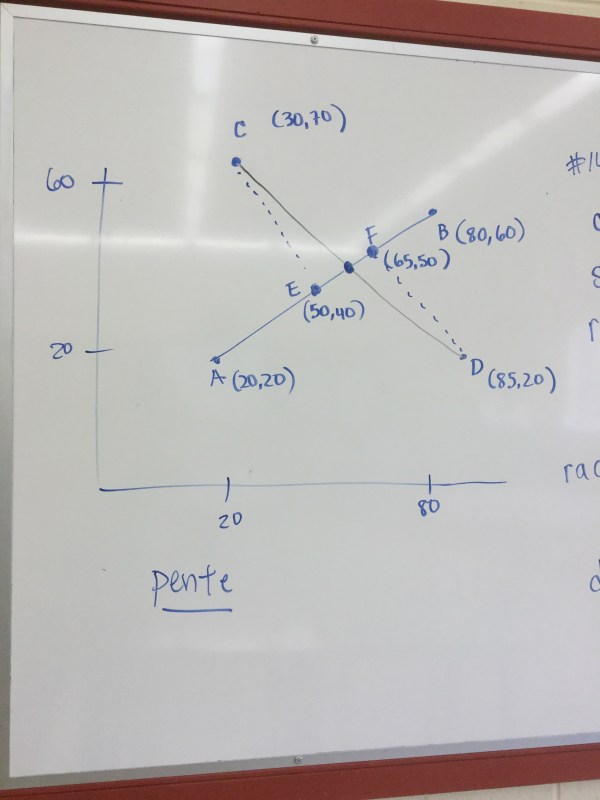
Grade 10s are working on problem solving, especially planning a good strategy.

We looked at how to decipher a problem to pull out important aspects that are hints for what strategies we may need.

We talked through some of the homework questions that had been challenging, and we also learned a new fact about quadrilaterals. If you join the midpoints of each side, the interior quadrilateral that is formed is always a parallelogram).

We calculated slopes and classified that the central shape is a parallelogram, and then we verified that it will always be the case by making a dynamic model with desmos geometry. We can measure angles and side lengths, and then adjust the drawing and see what happens to the side lengths and angles.

Today, in grade 9, we did some problem solving practice, in a new format.

We had a long row of desks, and we worked with our partner across the table. We used our formula sheets, and strategized to solve optimization questions, or composite volume problems, or pythagorean theorem problems.

After all problems are adequately solved, one side of the table is named the “experts”, and they stay put, while the other side stands and shifts to their right. They, the newcomers to the problem, will do the problem, with the support of the expert if needed.

The newcomer then is named the expert, and they stay put, while the other side, stands and shifts to their right, creating a new partnership.

This reciprocal teaching/review method works well for many activities. We’ll be doing it again regularly.

Today grade 9s had an interesting problem to solve. We investigated the cylinders made from a sheet of paper lengthwise vs widthwise. We compared the volumes of these cylinders.

We made the connection between the page dimensions and the circumference, and then calculated the diameter and radius.

We used the radius to calculate the volume.

And then we compared the two cylinders based on their volumes.

We did a lot of great thinking today!

Finally we consolidated and learned that the more cube like the cylinder, the smaller the area will be for a given volume. So when the cylinder’s height is equal to the diameter, the area is the smallest. Or for a fixed area, the volume will be the largest.

Act 1:

Act 2: photo

Act 3:

Grade 9s were tasked with creating rectangular prisms today with volumes that were 300cm^3.

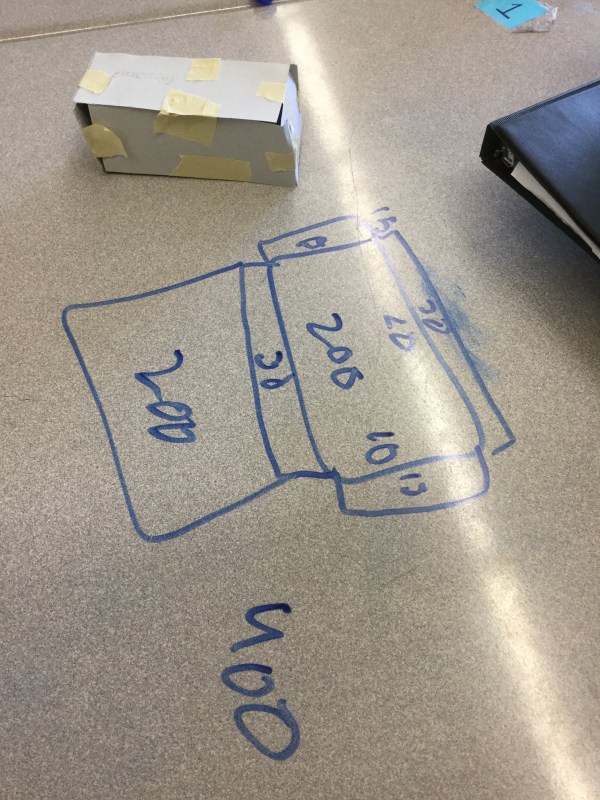
Many groups made plans first, then measured and cut out their boxes.

Each group had to then calculate the surface area of their prism.

And then were tasked with making another one, with the same volume and a bigger or smaller area.

After all of the prisms were made, we arranged them from smallest to biggest surface area.

We now know that if the volume is the same for two prisms, the surface area is not always going to be the same. The surface area can be bigger or smaller in number than the volume.

We noticed that the closer the dimensions get to being the same, the smaller the surface area gets (a cube is always the least area), and when the dimensions get really different (plate or snake shapes) the area gets big.

Applications of this are when we package objects, we aim for the most cube shaped box, to save money (less material needed for the box). We also can find this surface area/volume ratio in biology, as the reason for cell division, why we have dense spongy lungs, and why worms can breathe through their skin.

Good work today grade 9s!