How tall is the school?
Grade 10s used mirrors to explore similar triangles. They needed to apply their knowledge of the law of reflection with a plane mirror which was learned in science class.

We made a triangle with us (height to eyes) and the distance between the mirror and our feet. We had to be sure we could see the edge of the school roof in the mirror without leaning over.

Next we measured the distance between the mirror and the school.
 sometimes there were obstacles!
sometimes there were obstacles!

We then calculated the height of the school using similar triangles.

We were hoping to use shadows too, but sadly there hasn’t been sun during math class for the last week!
Math Dilemma… which one is the best price?





Commuter challenge
Interested in tracking some data? We’re looking at our carbon footprint as part of the commuter challenge. Sign up here.

All about angles
We used polygon tiles to build shapes and discuss angles. this first demonstration was more about fractions, but one blue rhombus is 1/3 of a hexagon, a trapezoid is 1/2 and a green triangle is 1/6 so we know that 1/3+1/6=1/2. We noted that the angles in the trapezoid and the rhombus were the same as the hexagon (120 degrees, since it’s regular) and the triangle had each angle as 60 degrees.

we made shapes that showed symmetry, and we also found lots of supplementary angles, and opposite angles to point out. We know that the angles around any point will add up to 360 as well.

This shape has rotational symmetry, and we were able to use the sum around a point being 360 degrees to figure out that the white rhombus has an acute angle of 30 degrees. We also noted that a lot of the sides are the same length, so that the shapes fit together nicely.

We also showed what we knew about opposite, supplementary, corresponding and alternate internal angles and transversals.




Finally we looked at an artistic bird image:

The task was to determine the dimensions of the shape we’d need to fill the negative space between the white rhombuses, and to calculate the area. A few measurements later, and we had it figured out! We’re always up for a neat challenge.
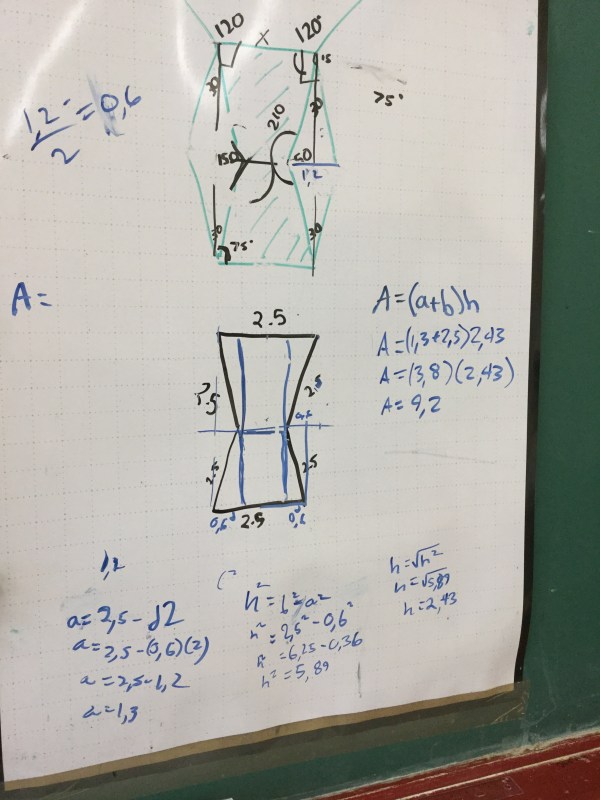

Solving linear and quadratic trigonometric equations
grade 12 are working hard to draw graphs and find intersection points using algebra, and then to interpret the intersections to make conclusions.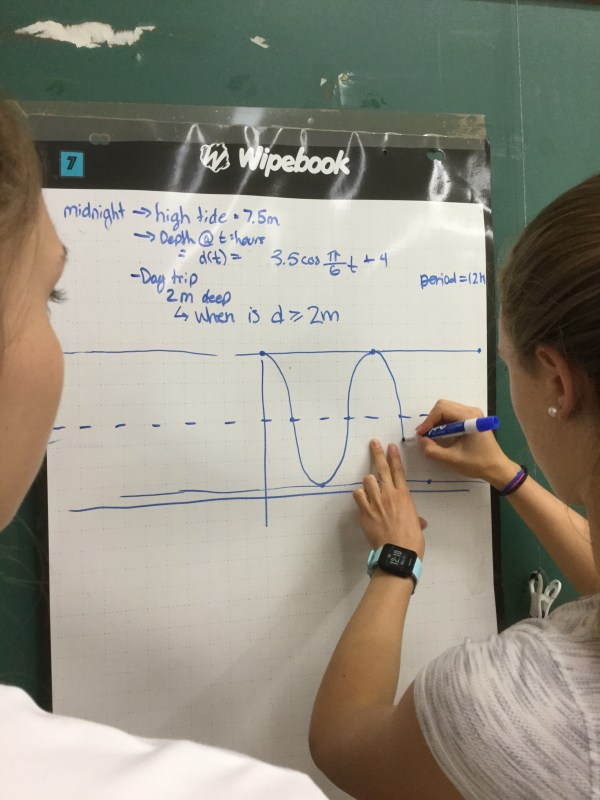


Lines and Angles
Grade 9s are working hard to review all their analytic geometry skills before their summative tomorrow.

We graphed lines from an equation (6x-2y=4) that we needed to rearrange first. We looked at calculating the x and y intercepts using various reasoning strategies using proportions, and also by substituting in zero for x or y and calculating the other.
We drew another line that was parallel (same slope) but different y intercept. We looked at how to calculate the x and y intercepts.
Next we drew a line through 2 given points (-5,8) and (3,-6). We calculated the slope, and the y intercept and then graphed the lines. Our last step was to label the angles and cut along the parallel lines and the transversal.

We noticed the acute angles we made are all congruent….so are the obtuse angles.


These angles are also supplementary (add to 180 degrees).
Look at the beans!

Graph Game
Grade 9s are working on Position Time graphs, and how the slopes of lines relate to the speed/direction of the object.
We’re looking at the graph game here
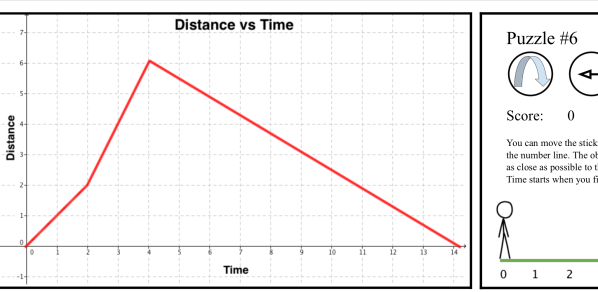
We need to slide the stick man in order to get the position time graph to match what is drawn. It’s a fun challenge.
Visual patterns
we’re practicing how to make equations from visual patterns in grade 10. We are using colours to show different terms. In this we have 2 n by n squares, and 3 groups of n in each figure. We see figure 1,2,3 shown.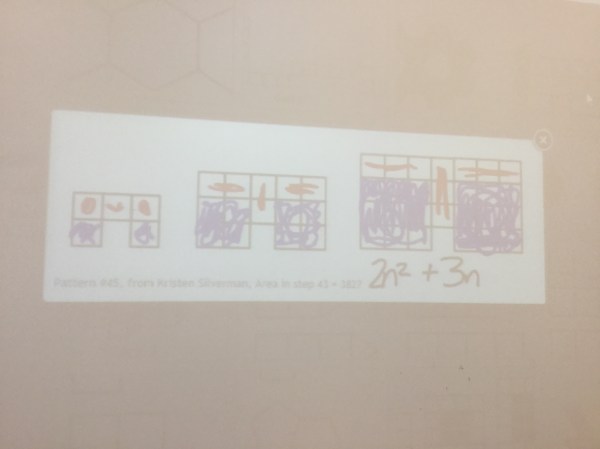 we can make tables of values and show that our pattern is growing quadratically, since the second differences are the same.
we can make tables of values and show that our pattern is growing quadratically, since the second differences are the same.
 sometimes there are a few ways to view a pattern, and we can make different equations (that would all simplify to the same thing in the end)
sometimes there are a few ways to view a pattern, and we can make different equations (that would all simplify to the same thing in the end)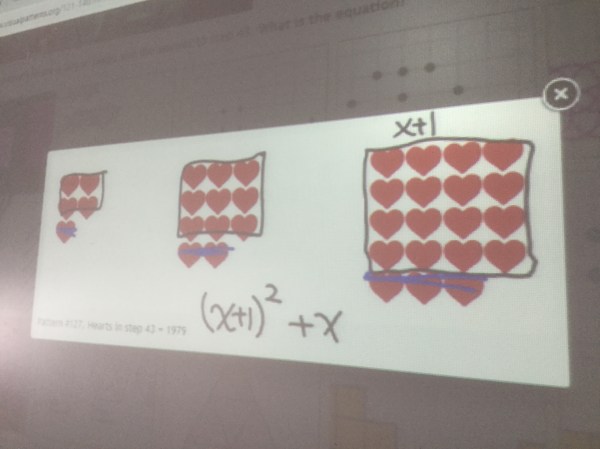 we looked at how to find the vertex of this equation. We decided to complete the square just to see if we could, even though the numbers are not so friendly. We use the same visual method, and use fractions or decimals.
we looked at how to find the vertex of this equation. We decided to complete the square just to see if we could, even though the numbers are not so friendly. We use the same visual method, and use fractions or decimals.

We could also have used the quadratic formula to find the roots, then found the axis of symmetry and then the vertex. It’s great there are so many options!
Eqao practice stations
We are working hard to get ready for our linear relations test and also practice EQAO questions at the same time.

We are getting better at using our reasoning to work through multiple choice problems

And we are showing our thinking in many different ways.
