Word problems
Grade 10s are working on quadratic word problems. We’re looking at maximum areas for fields, and maximum revenue for bushels of potatoes. In any situation we need to first identify variables, make an equation, or two, with the goal to make something quadratic. We are looking here for the maximum area or revenue, so we want to find the vertex (sommet) so we need to remember all the ways to do that, and hopefully choose a way that is quick. It’s often easy to find the zeros, the midpoint, and then the vertex. our revenue problem involved a farmer who started with 600 bushels of potatoes to be sold at 2$/ bushel. If she waits, she gets 100 more bushels a week, but the price drops by 10 cents a bushel. She needs to know when to harvest, to get the highest revenue.
our revenue problem involved a farmer who started with 600 bushels of potatoes to be sold at 2$/ bushel. If she waits, she gets 100 more bushels a week, but the price drops by 10 cents a bushel. She needs to know when to harvest, to get the highest revenue.
We can make a table and solve, but there are sometimes situations where a table becomes a very long tedious method. From the table we notice it is quadratic data. We notice that revenue is equal to price times number of items sold, and we also can make expressions for price and number based on waiting x number of weeks. using the table we see the maximum revenue occurs at 7 weeks. We also see the y intercept is 1200$. If we expand to make the trinomial we see the constant is 1200. We also noticed something neat. The 2nd differences are always double the “a” value of our quadratic.
using the table we see the maximum revenue occurs at 7 weeks. We also see the y intercept is 1200$. If we expand to make the trinomial we see the constant is 1200. We also noticed something neat. The 2nd differences are always double the “a” value of our quadratic.  We can use the trinomial form and the quadratic formula, or go back to the factored form and solve for the zeros, we could also complete the square..so many ways to get to the vertex! We find the ridiculous cases (the “stupid” case) where revenue is equal to zero. In this question if the farmer waits 20 weeks there will be lots of potatoes to sell but the price will have dropped to zero. If we sold 6 weeks ago the price would have been higher, but there would have been no potatoes to sell!
We can use the trinomial form and the quadratic formula, or go back to the factored form and solve for the zeros, we could also complete the square..so many ways to get to the vertex! We find the ridiculous cases (the “stupid” case) where revenue is equal to zero. In this question if the farmer waits 20 weeks there will be lots of potatoes to sell but the price will have dropped to zero. If we sold 6 weeks ago the price would have been higher, but there would have been no potatoes to sell!  we look to the graph. We can plot those ridiculous cases with 0 revenue, and then find the sweet spot in the middle where the revenue is maximized. We calculate the midpoint to be 7 and then can calculate the revenue when x is 7 by using our formula.
we look to the graph. We can plot those ridiculous cases with 0 revenue, and then find the sweet spot in the middle where the revenue is maximized. We calculate the midpoint to be 7 and then can calculate the revenue when x is 7 by using our formula.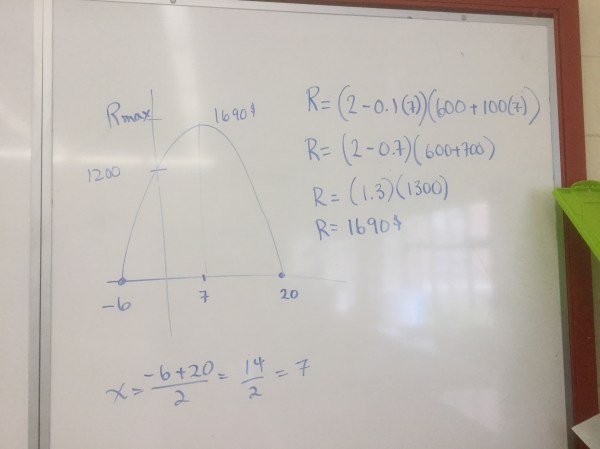
It’s a bit of a surprise for some of us to be seeing parabolas appear in problems that do not involve kicking a ball. We are seeing them in area problems, price problems, and patterning too. We follow the same steps as we’ve done before, but now need to keep a context in mind and make good choices of the path through the problem.
Speed dating
Grade 9s are working on graphing lines, and making equations for graphs.

We’re working across the table from eachother in “speed dating” style. Both partners solve the problem together, then one side stays as expert, the other side rotates and tries a new question. The first side helps their new partner to become an expert before they themselves shuffle to the next question.

There’s a lot of reciprocal teaching happening, lots of clarifying questions being asked, and some big “aha” moments!

We looked all together at how to calculate the constant (initial value/y intercept) when we have a line that passes through 2 points.
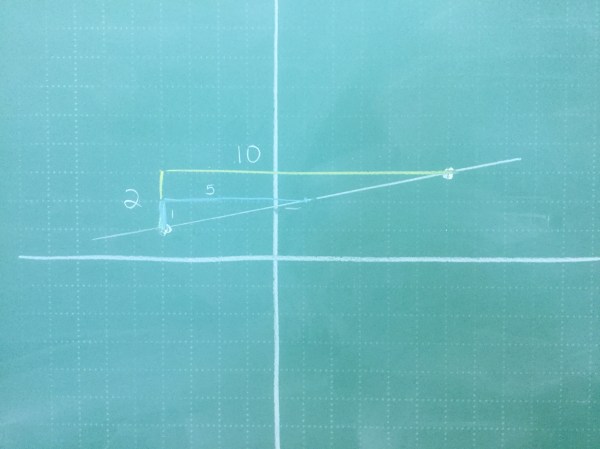 by graphing we could get close. We know the slope is 2/10 or 1/5 and we know that the y intercept is just less than 2.
by graphing we could get close. We know the slope is 2/10 or 1/5 and we know that the y intercept is just less than 2.
We can do better than that! Some of us figured that for each 1 square we move forward, we should go up by 0.2 since that’s 1/5. Using that logic the y intercept is 1.8
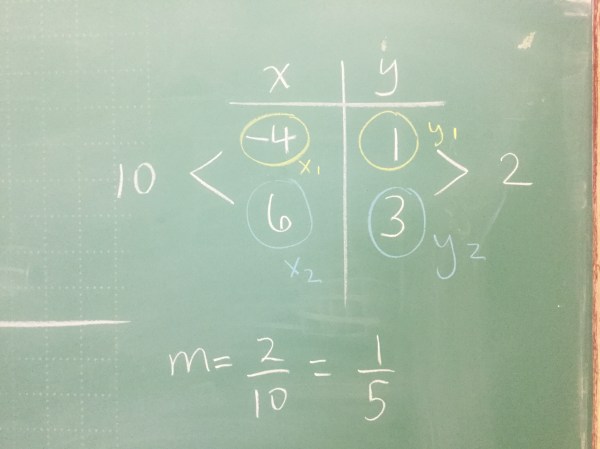
We looked at how a table can be helpful to find the slope as well. And how this connects to the equation for slope.

It’s all “rise over run” no matter how you look at it.

And the slope ends up being 1/5 again!

We can calculate the y intercept (b) by subbing in a point on the line for x and y. We then use algebra to get b.
 it doesnt matter what point we choose to use, b will be the same! 1.8 in this case.
it doesnt matter what point we choose to use, b will be the same! 1.8 in this case.

If we are not keen on algebra, we looked at how desmos sliders can be helpful, and also how desmos can do regression for us! Here’s a different equation, of a line that goes through the points that are in the table above. Technology is pretty cool!
All the forms of quadratics
Some quadratics work nicely in all forms. Here’s an example of one that can be factored, and also one that we can complete the square of, with no decimals. This is not always the case. Some cannot be factored, some have no roots. Some have a vertex (sommet) that has decimals. We can always complete the square, but it can be a lot messier than in this case.



Beans!

We have our first flower.
Multiple representations
Here’s an example of all the ways we can represent a linear relation. A visual pattern, an equation, a graph, vocabulary, and a table of values. The rate is shown in black, and the constant in green.
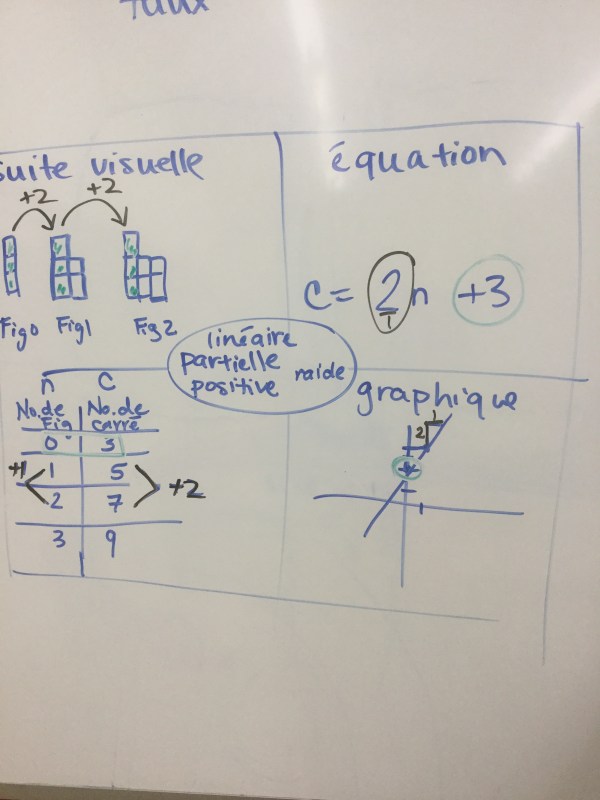
We worked on solving a problem in class too about a fridge repair. The first repair job cost 176$ and took 2 hours. The next job took 3.5 hours and cost 263$. We made a graph and found the rate (using the triangle). The price increased by 87$ for 1.5 hours of increased time. We looked for the unit rate which is 58$/h. The constant is found on the vertical axis, but we can’t know exactly what it is without some more calculations
 we can use our table of values and count backwards, for every hour we back track, the cost decreases by 58$. The constant is 60$.
we can use our table of values and count backwards, for every hour we back track, the cost decreases by 58$. The constant is 60$.
We can also make an equation with the cost and time. “B” is our constant, which we are trying to calculate. We substitute values that we know. For time we used 2 hours and for cost we used 176$. We already know the hourly rate is 58$/h. We can then calculate the value of “b” which is the same as we got from our table.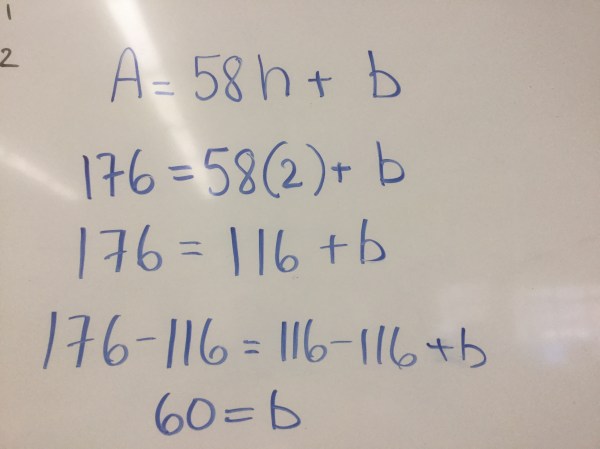
Applying our skills with lines

Grade 9s worked backwards today, given the graph of several lines, they determined the equations based on the constant, and the rate.
Their challenge then was extended to create lines that were parallel or perpendicular to the given lines. We’d seen parallel lines before and knew that they have the same slope. We have a call and repeat chant “parallèle” “même pente” that we have engrained in our long term memory.
Some of these lines were tricky since we couldn’t read the constant on the graph, we needed to use our reasoning skills to determine the equation.
Our new chant of the day is “perpendiculaire” “inverse négative” which means we take the slope of one line and flip the fraction, and multiply by negative 1. In English that is called the “negative reciprocal”.
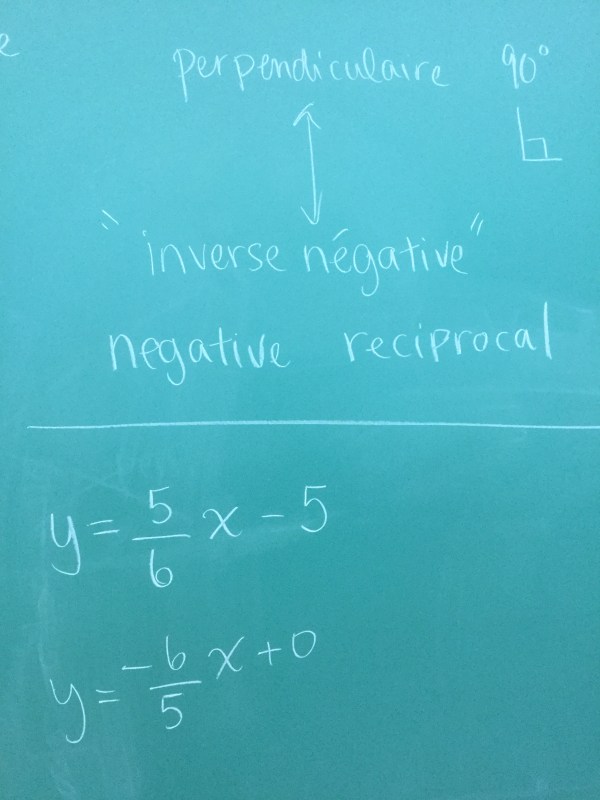
The second equation is perpendicular to the first, and also direct.
We looked a little at different ways of managing if the line doesn’t look like y=mx+b. We can either do some algebra to isolate y, or we can use the x and y intercepts to graph the line.

Here’s the algebra to isolate y.

And here’s how we can find the intercepts. We know that the equation of the x axis is y=0, and the equation of the y axis is x=0 so we sub x=0 and solve for y, and also y=0 and solve for x.

We can see how all of this makes sense on the graph

Busy day today learning a lot!
Clothes line activity
 grade 12s are developing their comfort with radian measure. Today we made a proportional clothesline of radians. We taped all the cards to the string, and then made the string into a circle to check our work.
grade 12s are developing their comfort with radian measure. Today we made a proportional clothesline of radians. We taped all the cards to the string, and then made the string into a circle to check our work. we noticed that 2pi and pi are directly opposite, and so are (pi/2) and (3pi/2). We did a pretty good job with our spacing.
we noticed that 2pi and pi are directly opposite, and so are (pi/2) and (3pi/2). We did a pretty good job with our spacing.

Our new favourite song
We completed the square of the general standard form equation today. We then set y=0 to solve for the roots. 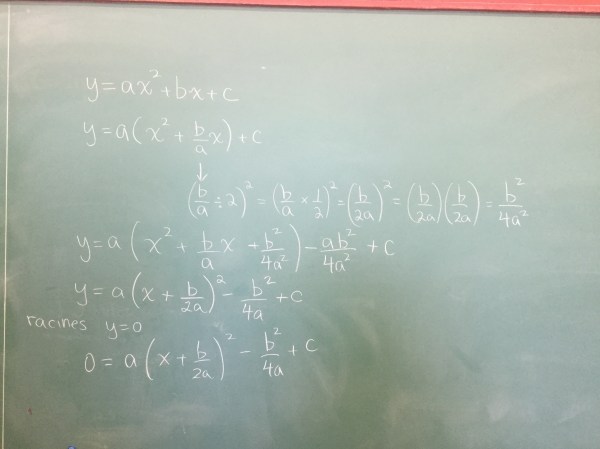

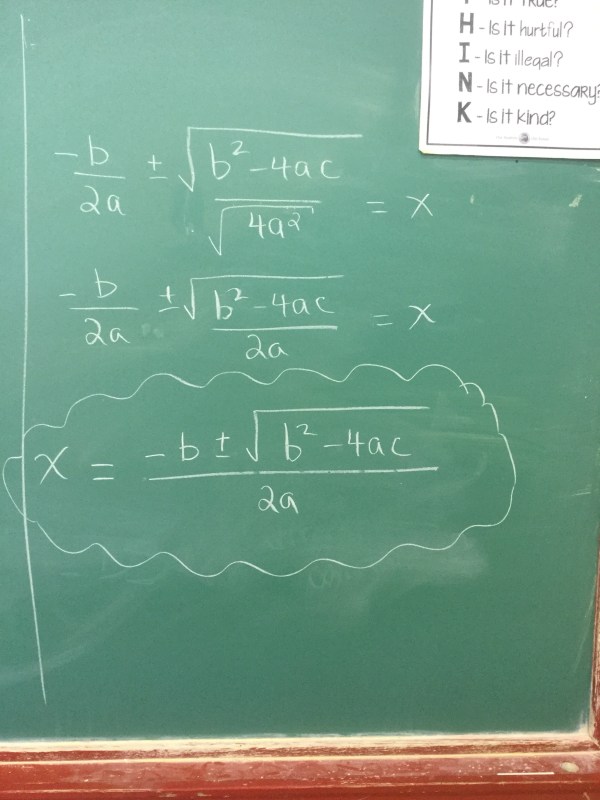
It’s a complicated procedure, but in the end gives us our new favourite formula (which can be sung to pop goes the weasel). We looked at how to sub in “a”, “b” and “c” and how what is under the square root is really important. It tells us how many roots there are.

Lines, lines, lines
we looked at lots of lines today, some were direct, like this one with a constant of 0, we noticed the rate triangle which shows that the line goes up by 2 for every one it goes over. We also looked at how each point has coordinates that satisfy the equation, so if x=5, y=(2)(5)=10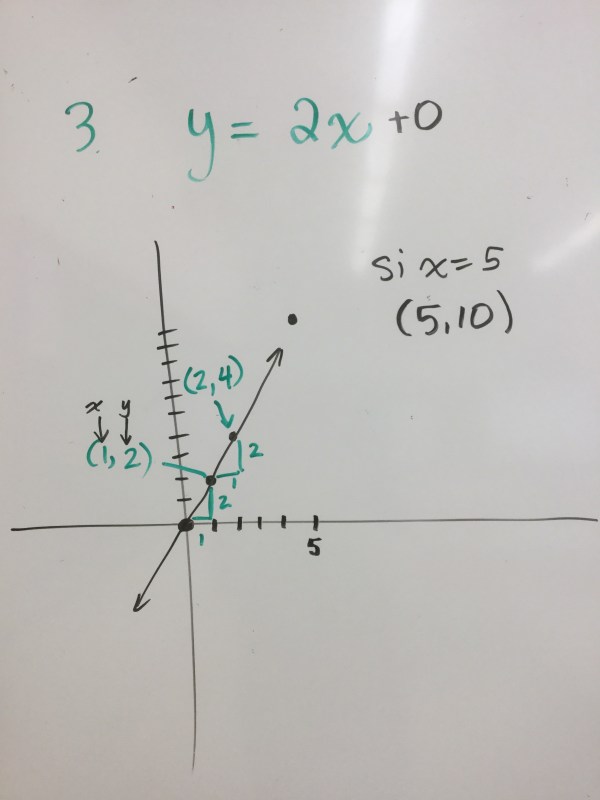
We saw that if the rate is written as a decimal or a fraction it’s the same thing. The line can go up by 0.5 every one time it goes over, or it can go up by 1 every time it goes over by 2.
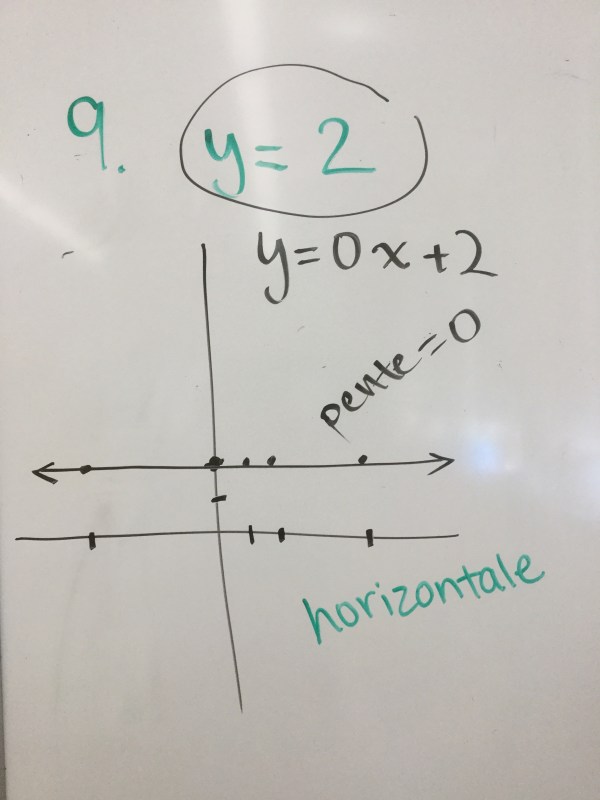
We saw how if there is just a constant, the rate is 0 so it is a horizontal line.
And if there is x=a number for the equation, it’s a vertical line.
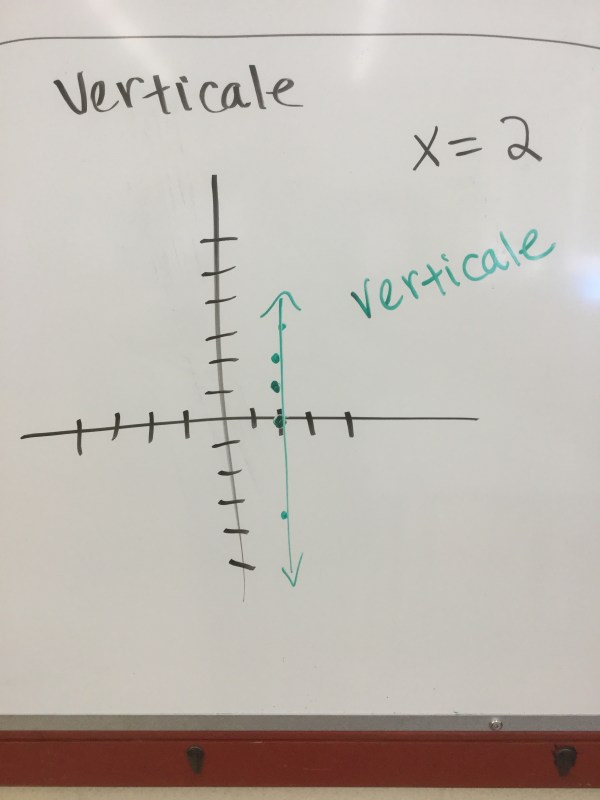
We looked at how helpful desmos can be for graphing lines, and for telling if an equation is linear or not.
Speed dating for review
In grade 10 and 12 today we did a speed dating style review. Paired up, we looked at solving problems.

Grade 10s were looking at features of parabolas given different forms of the equations, completing the square, and factoring. Grade 12s were working on special triangles, graphing trig functions, and solving problems all using radian measure.
After working on a problem, one side of the partnership shifts one space to their right, and tries the next problem with support from the expert who stayed behind.

A timer is set, and after the 5 minutes is done, the other side of the partnership shifts one space to THEIR right to create a new partnership. Each person gets a chance to be the expert, after having been supported through the problem. Each person gets opportunities to work with many different partners.

Students become better at pacing, better at giving good clues, and asking good questions, communication improves, and 72 minute classes pass by pretty quickly when done in this format!