Multiple representations
In grade 9 we’ve been working on patterning. We use visualpatterns.org to supply some patterns, and we are getting good at making our own as well.


Those two show examples of what c=3n+1 looks like. The constant is 1, and we see 3 groups of “n” (the figure number) in each figure. We also notice that each pattern adds 3 each time, so it is linear, growing at a consistent rate.
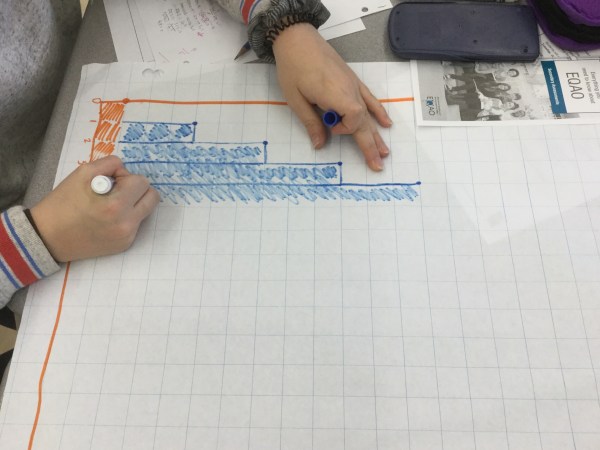
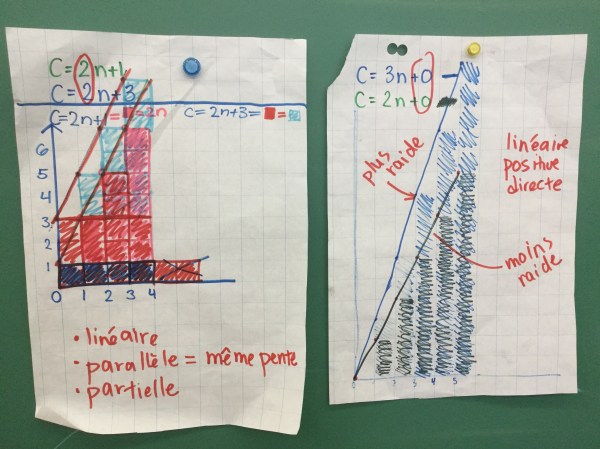
We placed the squares from each figure on the graph, and coloured in the column. We showed the constant is always there (in orange here), and it doesn’t change. The number of blue changes, it goes up by 3 each time. This corresponds to c=3n+1. We noticed that it is partial, that the constant is the initial value on the vertical axis, and that the rate of increase is 3 squares for each increase of figure number.
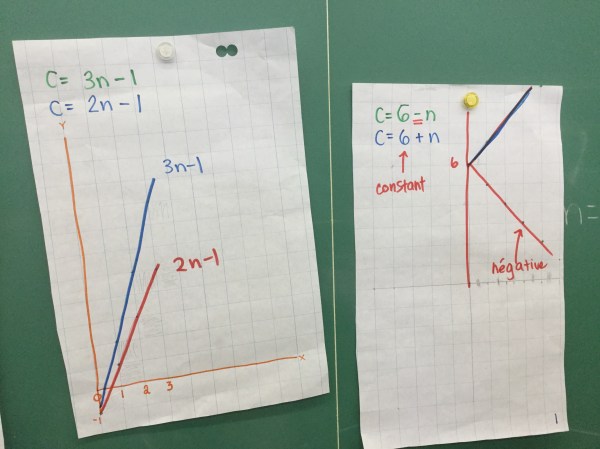
Each small group was then given 2 equations to draw, and notice things about. Here the constants are different, and the rate is the same. The lines are both positive, partial, and also parallel.

We looked at some with negative constants, and different rates. If the coefficient is bigger we noticed that the line is steeper. The other graph shows the same constant, of 6, and one with a positive rate, and another with a negative rate. That was a bit tricky to figure out how to manage a rate of decrease.
We noticed that if the constant is 0 then it is a direct graph, passing through (0,0).
We did a lot for our first day graphing lines! Good job everyone. We can now connect the representations of visual pattern, equation and graph.
Different forms of quadratics
Grade 10s are working hard to determine the key features of parabolas from different equation forms, and vice versa. We looked at working backwards to create equations given different graph features.

We used symmetry to determine one zero when we knew one zero and the vertex
We worked through all the forms, starting with creating the vertex form equation. We substituted the values of the vertex, and then the given root, we subbed in for x and y. We calculated “a”.

The next form was factored form, so we needed both zeros and a point (the vertex) and we subbed in our values and calculated “a” (which was the same as before! We noticed “a” is the same in all forms).

We expanded to get standard form, and saw the y intercept, the “c” value

By plotting this equation on desmos, we could verify that the vertex and roots were what they were supposed to be.
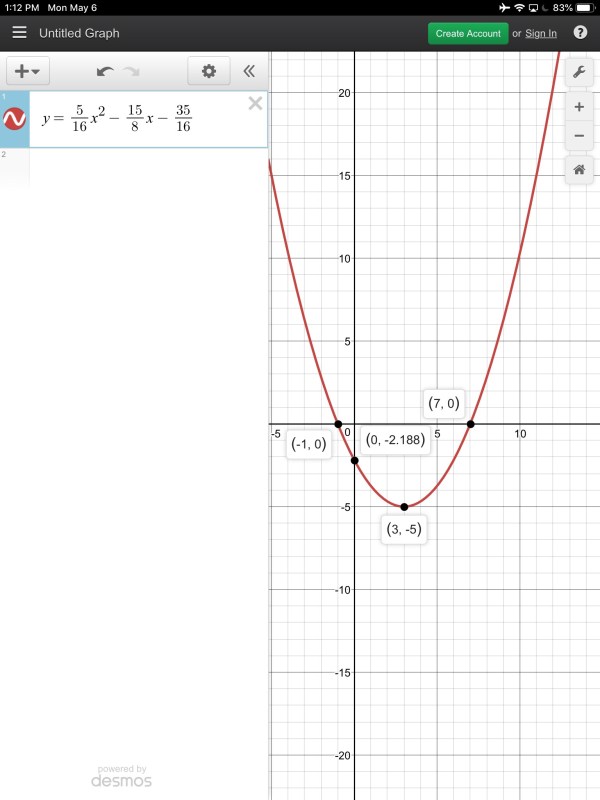
It’s pretty elegant how all of these forms fit together!
Completing the square
Grade 10s are getting skilled with using vertex form, and we are now learning how to change an equation into vertex form, by completing the square.
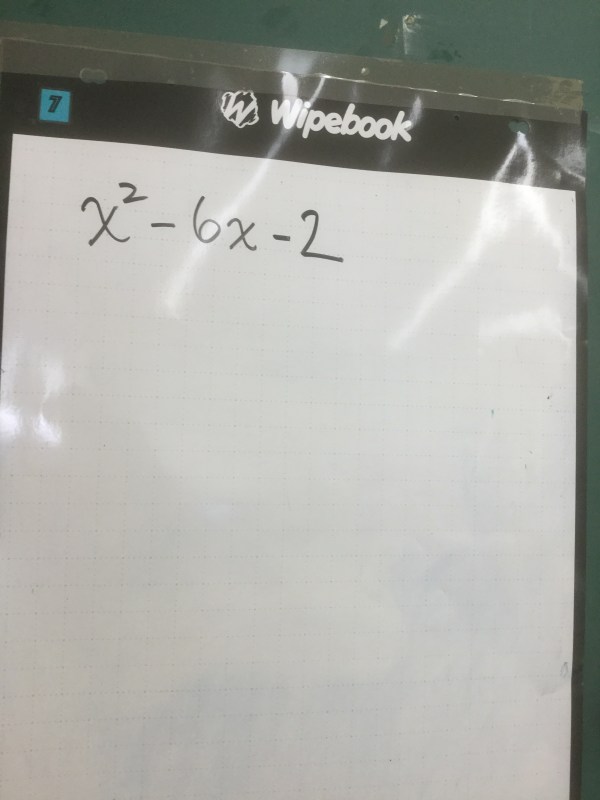

Step 1: represent the trinomial, and in this case we always want to make a square, so we split the x term in 2 groups, and use those for the sides of the square. We need to fill the square with 9 red squares. In order to get 9 red squares we need to add 9 zero pairs.


Our final equation in vertex form is y=(x-3)^2-11
Here’s another example: x^2+4x+1

We need to complete the square with 3 more red squares so we add 3 zero pairs

And complete the square

Our final form is y=(x+2)^2-3
Patterning
from the same drawing of figure 2 we were able to create many different patterns. Some grew by 2 with a constant of 1.
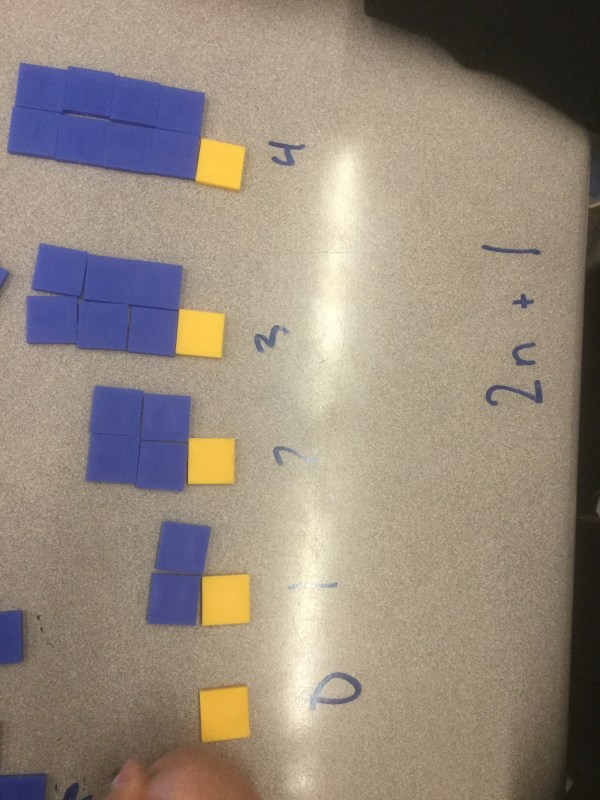
Some grew by 1 with a constant of 3

Some grew by 2 with a constant of 1, but in a different way than before…

We looked at how to know if a pattern is growing linearly, by adding the same thing each time to get to the next term
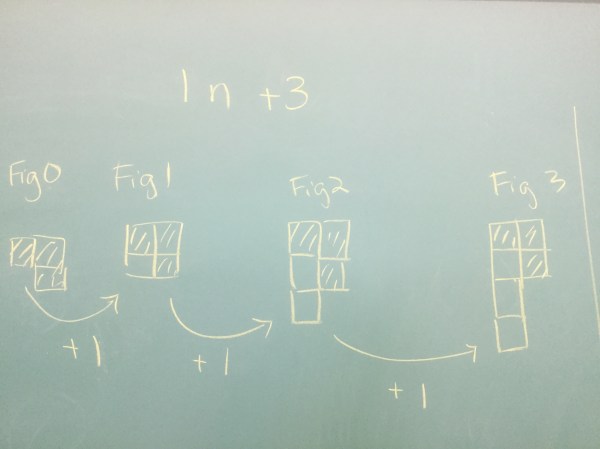
Or non-linearly by adding different numbers of squares each time. In this case, we look for squares of “n” as well as groups of “n” to determine the equation (which we do lots of in grade 10).

We explored visualpatterns.org and found some patterns quite tricky. This one has a constant that is negative!

We will be looking at patterning and how patterns relate to equations and graphs over the next little while.
Modelling equations

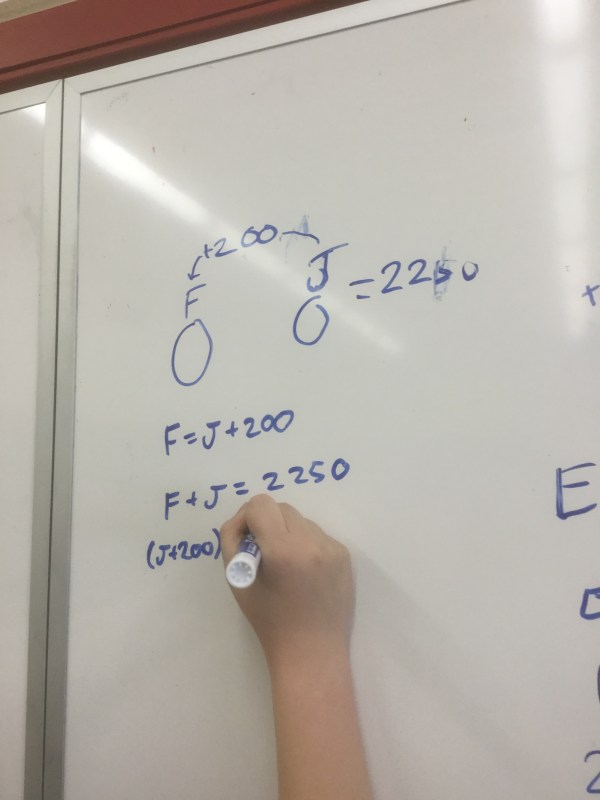
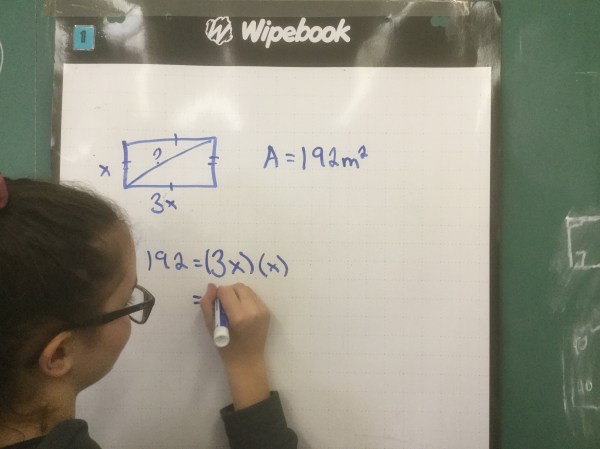
Figure this out!

Grade 12s were looking at what equation would be needed to create this graph. Good luck for the test tomorrow grade 12s!
Photos of today’s review (grade 10)








Determining growth rate

Grade 9s looked at their bean graph to try to determine the growth rate for kidney beans and black eyed peas.
We noticed that the red beans grew earlier, and faster than the black eyed peas. This meant that their points made a steeper line of best fit, and their x intercept was lower than that of the black eyed peas.

We saw that sometimes for an individual bean the trend was not linear. More often than not the bean started at a higher rate, and then grew less and less each day after a certain point. This trend is non-linear. We did not have any magic beans that got increasingly tall each day by a bigger amount.
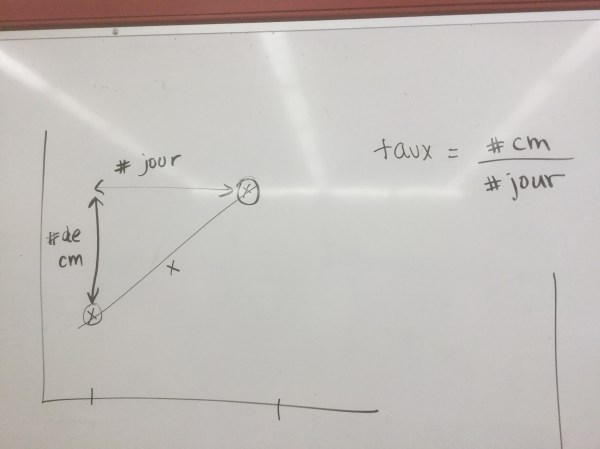
We looked at how to find the growth rate of a bean between 2 days. We calculate the number of cm grown and divide that by the number of days elapsed between measurements.
For the group of beans we can do this for our line of best fit.

Some groups found many averages

We looked at how to do a regression on desmos. We can make desmos do the figuring for us, and come up with the line of best fit. We can use the line created by desmos to do interpolation and extrapolation. We can also notice the intersection point. At that time the two plants were the same height (on average).
Technology can save us a lot of time!
Grade 10 word problems


We looked at question 7 together. The steps we use:
1. Make a picture
2. Introduce variables and make an equation or maybe more than one
3. Trinomial=0
4. Factor
5. Parentheses=0
6. Solve
7. Concluding statement


Solving Big Equations
Grade 9s are working on equation solving today.

Here’s an example of a solution. We tried some pretty complex problems, involving lots of simplification, and even fractions.

We looked at how to divide fractions, or how to multiply by the denominator to eliminate the fractions…
We also looked at what fractions mean, and how we can represent them

We looked at what a negative fraction means, and realized that it doesn’t really matter where the negative sign is within the fraction.
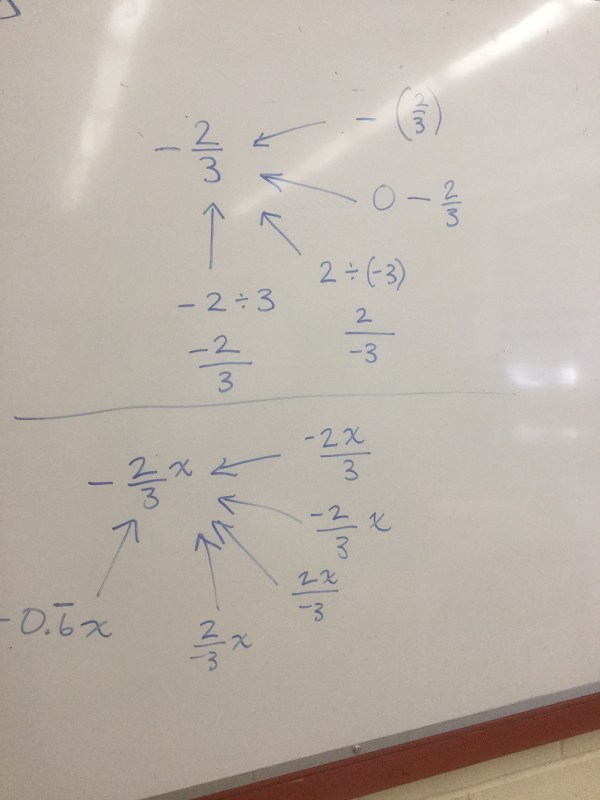
We’ve got a quiz tomorrow to check our understanding.