Ms. Bearse's Site

Grade 10s are working on making good strategies and presenting their thoughts clearly.

When given 4 points we try to determine the type of quadrilateral.  Sometimes a freehand sketch can give us enough information, other times we need to reach for a grid.

Other times Desmos is faster.

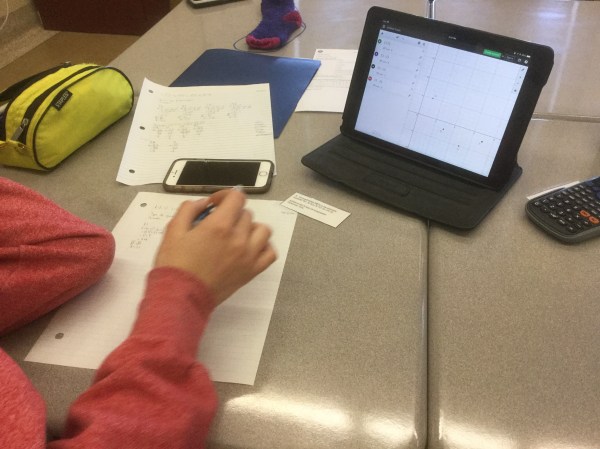
We then use our tools (calculating slopes and distances primarily) to work through whatever challenges we are given.

We are getting better at organizing our thoughts so we can check our work, and our peers can follow along.

In grade 12 we are working on our long division skills using polynomials.  We are going to be able to use these skills to help us factor cubic and quartic functions.

Grade 9s challenged themselves today to calculate the volume and surface area of this container.

The container is not a rectangular prism.  The square base on the bottom is larger than the square  base on the top.  The following measurements were provided:  the side length of the bottom square was 12.5cm

The side length measured along the edge was 21cm

And the diagonals of the top square are 12cm

We worked hard and realized quickly that the pythagorean theorem would be important on several occasions!  We also needed to use our area of a trapezoid song!

Some groups noted similarities to a pyramid, but one that had been chopped.

We noticed that it was going to be hard to figure out the height of the pyramid.  The ribbon attached turned out to be a very lucky length!

We measured the ribbon (77cm) then worked on figuring out what we’d be able to figure out with that information.  We used string on the pyramid model to help us visualize our ideas.

We planned to calculate the volume of the large pyramid and subtract the volume of the small pyramid.  We used the pythagorean theorem again using half the ribbon length as an addition to the original height of the trapezoid which combined to make the total slant height of the pyramid.  

We learned that a cubic centimetre is a millilitre, and used that to convert our volume to litres.

We compared the container to known volumes (nalgene bottles, or 2L bottles of pop) to check for how reasonable our answers were.

One group tested their volume calculations by repeatedly filling  a 1L water bottle and dumping it into the container.  By doing this slowly, they determined that they had over estimated the capacity of the container, and would have had a big puddle on the floor if they had actually poured close to 3L into the container.  

Best quote of the day: “this math class is more fun than my music class!” 🙂

We hit the ground running today looking at polynomial functions.  We are getting comfortable drawing graphs from factored form, and determining equations of graphs that we see.

We are remembering how to factor too!

We did a card stack review activity.  Each card has an equation on one side and a graph on the other.  The card are all placed graph side up, one card is flipped, and then we need to find the graph that matches the revealed equation.  When the graph that matches is found, it is flipped onto the pile to reveal a new equation.  This continues until the pile is complete.  The equation at the top will match the graph on the bottom of the pile.

We have developed a good sense of intuition!  Next step is the fun of factoring 🙂

Today we focussed on solving problems.  Whether our problems are in life, or in math, we have similar strategies!

Gather information

Organize information

Make a plan

Check to see that the plan is working

Ask for help if needed

Check to see that the problem is solved

Our problems we are solving now are based on coordinate geometry.  We can calculate many things (slope, midpoint, length, perpendicular bisectors, medians) and we can do these calculations for various segments (side lengths, or diagonals of shapes).  We need to really be clear about our plan, because we can waste a lot of time if we get off track.

We are classifying triangles, calculating area and perimeter

We are classifying quadrilaterals, and looking at their diagonals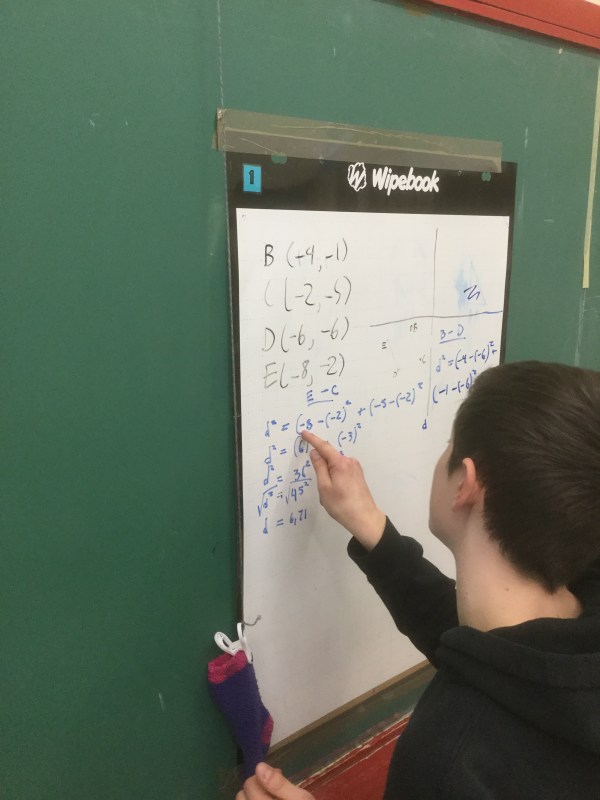
We are working hard in our groups to solve the problems, and to check our work and present our thoughts in an organized way.

Today we developed the formula for calculating the volume of a sphere using a tennis ball and a juice container, some water and a displacement tank.

The important thing to know is that a juice container has the same radius as a tennis ball.  We cut the container so that it is the same height as the tennis ball too.  The height of the cylinder is the same as the diameter of the cylinder, or 2r.

We fill the displacement tank and let it drip until the water is just at the level of the spout.

When the water stops flowing from the spout, we place the empty juice can under the spout and then we submerge the tennis ball, and press it down under the water.  The water displaced by the tennis ball will flow into the juice container.

The water stops flowing, and the container is 2/3 full.

Here comes the math:  the volume of the cylinder is V=(pi)(r)^2(h), but remember h=2r since we cut it.

V=(pi)(r)^2(2r)

V=(pi)(r)(r)(2)(r)

V=2(pi)(r)^3

Now we know that the sphere’s volume fills 2/3 of the cylinder

Vsphere=(2/3)(2)(pi)(r)^3   And we multiply the (2/3) and the (2)

Vsphere=(4/3)(pi)(r)^3

We also started an experiment today!  We are going to see if beans will germinate.  We have several kidney beans and black eyed peas, and have put them in paper towel and in a baggie.  We will check in at the end of the week and see the percentage that germinated.

We also looked at bumping up our portfolio writing.  We have submitted one task already, but have a chance to make it better using the feedback we received.

We looked at some composition samples, and highlighted all evidence in yellow, all reflections in green, and all summaries in orange.  We looked at our rubric, and determined where we could add more supporting details, and improve the writing.

We have another composition to do next week, and we’re feeling more prepared!

In grade 9 today we celebrated pi day by looking at circles, measuring diameter and circumference and making a scatter plot.

We made a line of best fit using desmos.

Next we looked at the surface area of spheres.

We traced oranges to make circles with the same radius as the sphere.  We peeled the orange and filled the circles with the peel.

We filled 4 circles.  Each circle has an area of pi(r)^2, so this explains why the formula for the area of a sphere is 4(pi)(r)^2.

Grade 10s looked at the equation of a circle, and how a circle is defined by the equation x^2+y^2=r^2.

Grade 12s did the tootsie pop experiment.  The initial circumference is measured.

After sucking on the lollypop for a minute, the circumference was measured again

We kept a table of data

And now we are going to make graphs comparing circumference to time, surface area to time, and volume to time.

Happy March Break every one!  Have a happy Pi Day on March 14. (3/14)

Here’s the recipe I used for the butter tarts we ate today.

1 1/2 cups packed brown sugar
2 eggs
1/2 cup butter
2 cups raisins
2 tablespoons heavy cream
30 (2 inch) unbaked tart shells

Preheat oven to 325 degrees F (170 degrees C).

Cream the butter, sugar and eggs well. Add remaining ingredients and mix thoroughly.

Pour batter into tart shells, no more than half full. Bake for 20 – 25 minutes. Watch carefully!!–they’ll burn quickly. 

Divers in flight are pretty close to tangent lines to a parabolic trajectory.

We watched some fast races, all timed to the 100th of a second.  We recorded split times (every lap) of the races for our swimmers so we could compare speeds (distance/time) for the different sections of their race.

We watched divers practice from the platforms, and they we able to rotate and flip so many times as they fell.  I wondered how much water was in the pool, and how heavy that’d be.  I also wondered about how many tiles it would take to cover all the surfaces.

Hello Grade 12s,

Here’s the code for your desmos activity today.  Make good notes! 

Période C: Mercredi

Bonjour les 10e: Dans vos groupes, notez les choses que vous REMARQUEZ et les QUESTIONS que vous avez/que vous voulez répondre.

ACT 2: Vous allez faire le travail!

Quelle information voulez-vous savoir?

Faites les estimations de ces dimensions dans vos groupes.

This slideshow requires JavaScript.

Voici les dimensions:

This slideshow requires JavaScript.

Maintenant, déterminez la longueur de la corde que vous avez vue dans la première vidéo.

Act 3: Voici la réponse