Paper Planes
We looked at intersection of planes this week in calculus and vectors. To test our knowledge groups got a system of 3 planes and used their skills to determine if the system was consistent (there was a point/line/plane of intersection) or whether the system was inconsistent (no point/line/plane of intersection) and how.
The next step was to cut out their system, and slide the pieces together to see how the planes intersect.

We had 4 groups and 4 different results.

It was a fun way to visualize what our matrices told us!
Problem Solving Review
My class of grade 10s has come a long way since February, in terms of math skills, confidence as problem solvers, and our sense of community in our classroom.
Today we started looking at some interesting problems that mix a lot of ideas together. It’s a nice way to end the term, and show them how far they’ve come. We also get a good exam review by doing problems that involve many aspects of our course.
To start the class we looked at what types of math we’d learned, and what are some of the key words or equations or strategies they might need.

After listing all this we started to work on our first question.

We needed to do a bit of brainstorming with our groups. What type of question is this? We noticed key words, and units. The word angle made us think of trigonometry. The squared units made us think of area and quadratics. The 2 equations for perimeter and area made us think of substitution. We know we need to make a diagonal line, and we know diagonals join opposite corners. We need a good picture and some variables and some equations!

what happened next was magical. Groups got to work. Independently, and collaboratively. There was such a hum of activity in the room.

It’s a pleasure to be able to stand back and watch them work, but also it’s great to interact and see and hear what each group is thinking. There are good questions being asked, and students are helping each other to know what the next step is. They are checking to see if they are on the right track, and reassuring each other. They are checking to see if their work is reasonable, and what’s even better is that they are having fun with each other and also with the math.

In this particular question many students questioned if we are looking for x intercepts or for the vertex. There was good conversation about what to do with 2 positive x values as roots to their equation. We talked about if we could use sine cosine or tangent or if sine law or cosine law were better.
we moved on to look at some questions with systems of equations and percents

Here’s a group mid trouble-shooting…they are figuring out why they ended up with a negative value. They figured it out…it all had to do with how they set up their equations to start with. Hopefully by working through these situations now, if it happens on a test they will know what to check for and how to correct it.

The next problem we did was one involving rates and trigonometry.

I added an extension for groups who finished early, asking how far the boats would be from each other after 45 minutes. This allowed us to enter into a nice discussion about similar triangles.

We had almost everyone engaged in problem solving for almost all of the class today. We’ve built up this stamina over time. It’s a process, but at the end of term it’s great to see how far we’ve all come.
It felt good today. Hopefully this can continue into tomorrow’s review as well.
Exam review begins
We’re blending our final rest review into our exam review. This is one of the joys of spiralling the curriculum material. At the end of the year we are doing exam review for quite a while, and everything has been covered recently, so there’s less of an issue with forgetting major concepts.
Today we looked at solving some word problems.

We are working on connecting our knowledge of quadratics to the context of word problems. We’re remembering lots about different forms of quadratics, and what we can read quickly from equations, and what needs a bit of calculating.
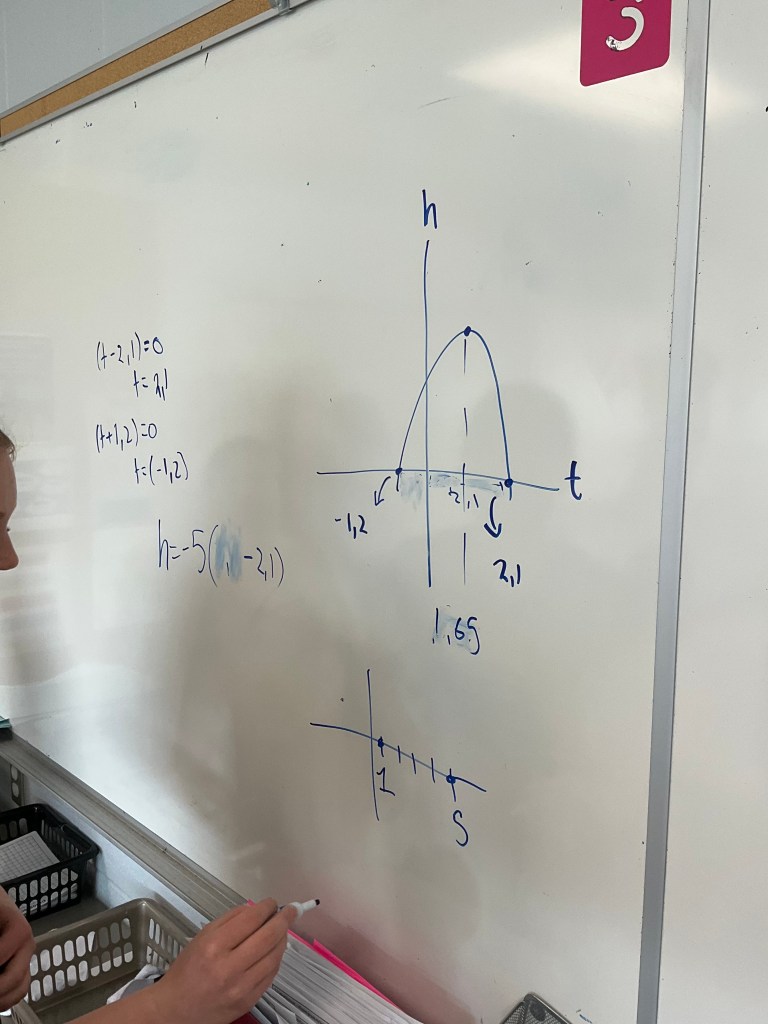
It’s great to hear the students working together and helping each other. We have so much expertise in the room!
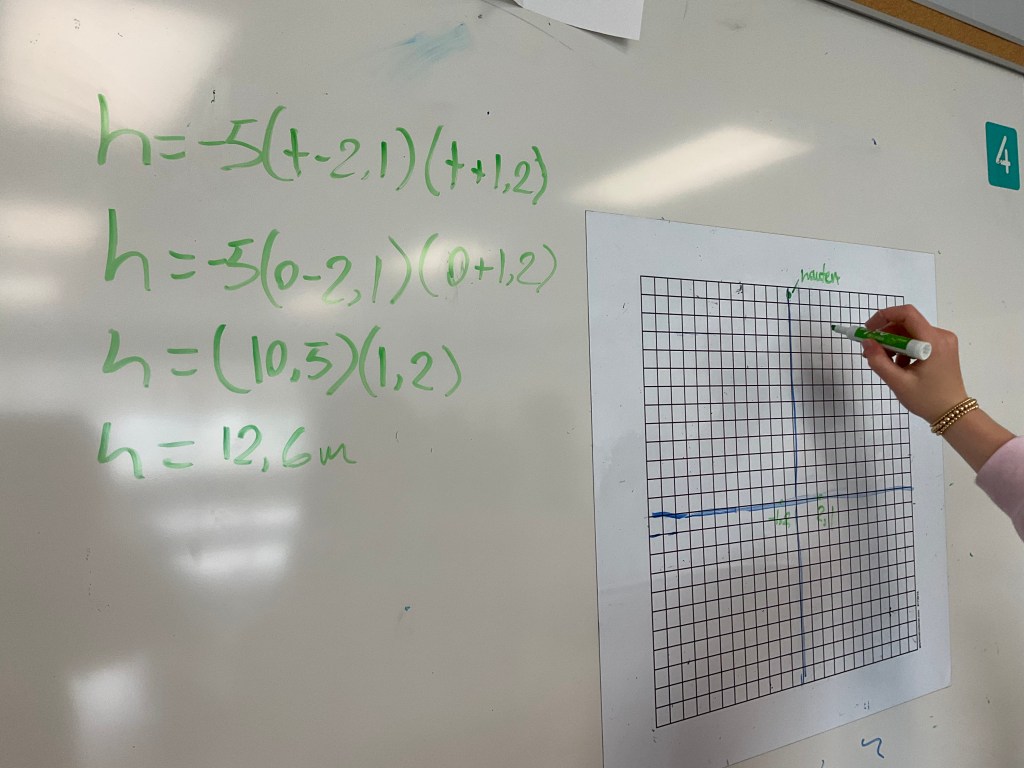
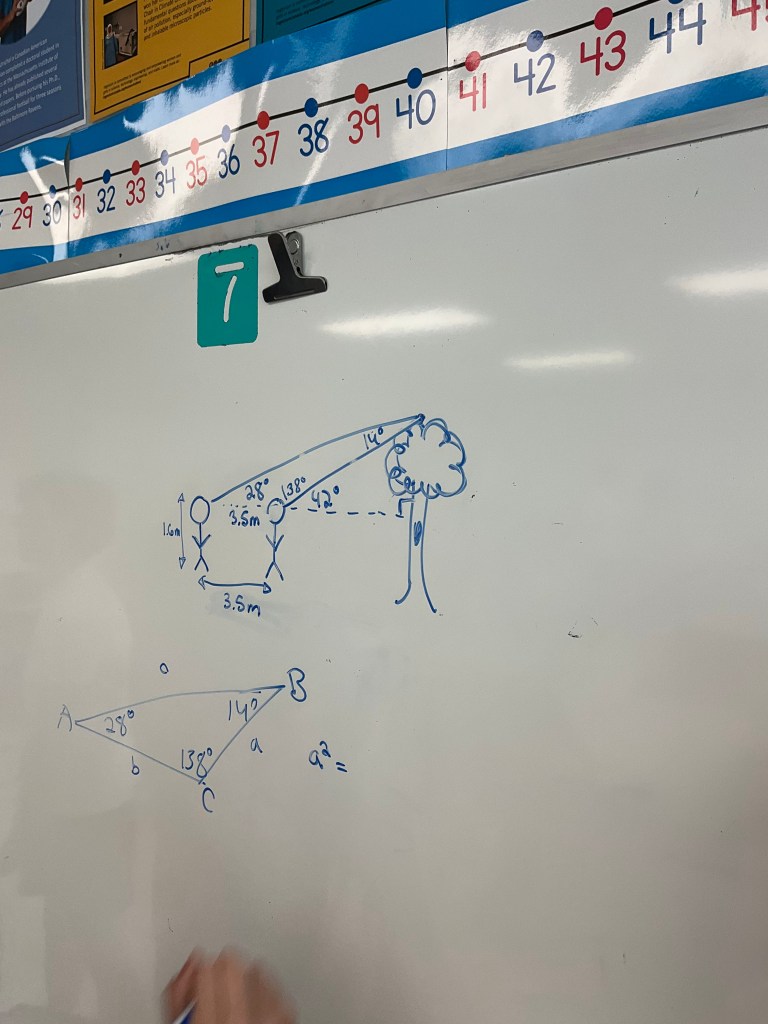
We looked at a trigonometry word problem too where we needed to draw our own picture.

We’re getting better with translating words into pictures, and making a plan to solve.
We’ve come a long way since February!
Catapult Results
Today we looked at our catapult results for the entire class.
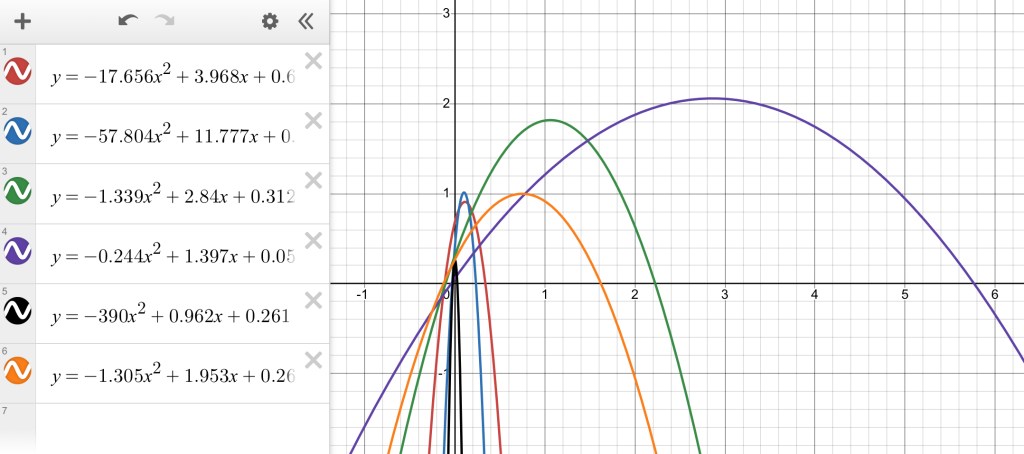
It was interesting to see how varied the results are. Some groups had to work in the atrium to have a bigger height, since they kept hitting the ceiling. It had the farthest range, and the highest vertex.

Other groups with closer x intercepts had much more repeatable experiments.

We have practiced doing lots of calculations to be ready for our individual portion of the task on Monday.
Tech Weigh In: 3 act task in vectors class
Today we did a 3 act task in grade 12. It’s one I have done in grade 10 before, but this time I introduced it as a way to review elimination, and to introduce matrices as a way to solve a system of equations.
Here’s act 1: to set the scene
There are 3 parts to act 2
Each scenario gives enough to build an equation. Groups tended to do elimination at first, and then substitution to follow, or substitution at each step.

We need to work on our elimination skills so we can use matrices and understand how to reduce them. We’ll keep working on that tomorrow.
At the end of the lesson we looked at act 3 to check our answers to see if we were close.
Catapults: Culminating Task in Grade 10
In grade 10 we started working on our culminating task: analysing the trajectory of catapults that we build in class.
Today we started building and testing and collecting data.

Each group gets about 10 tongue depressors or popsicle sticks, a plastic spoon, several elastic bands and some tape. We use painters tape because we are aiming for something that can be disassembled, so the pieces can be used again next term. Each group also gets a target, a pompom, and a package of work to do.
After they have created a catapult (with or without online tutorials) we go into the hallway and collect some data.
We film the pompom being catapulted, then use the app Visual Physics to track it.

Here’s a different one being tracked. We need to scale the image (that’s why there’s a meter stick on the wall). We need to touch the screen where we see the pompom (we track the leading edge of the blur). The program advances time slowly so we can see the pompom at many points along its trajectory.

Finally we upload the file to a different app where some analysis can be done. In this case we can see a table of values, and a graph with a smoothed quadratic overlayed. The a b c values are given for the quadratic.
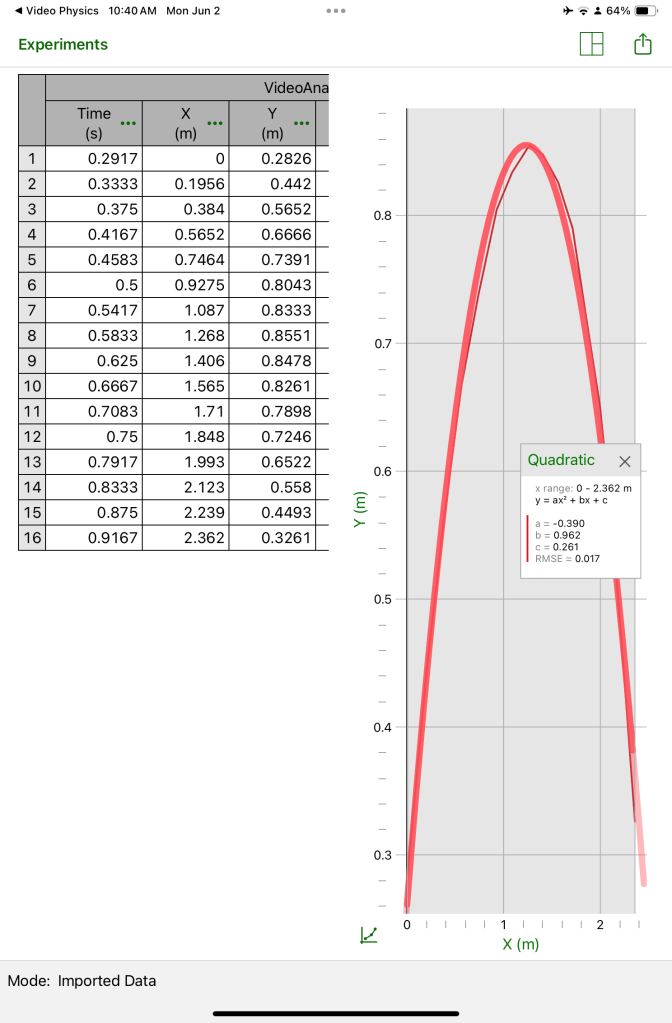
The next step for students is to see if they can use the table of values to calculate a similar “a” value to the one the program gives. Also they use both equations to calculate where the pompom lands.
The extensions are questions like: if the catapult was on the floor and trying to hit a target on a chair, determine how far back the chair should be. If the catapult is on a desk, where should the target be on the floor? By adjusting the initial conditions we can play around with how that changes our calculations.
After working in groups for a few days, we will each try to do something similar individually as part of the culminating task.
PD presentation
This morning my colleague and I presented some of our OAME presentation to our staff at our PA Day.
We were tasked with having an ice breaker, and then sharing some of our work on mindset and creating brave spaces for our students.
We started the day with random groups done by team shake, to have everyone mixed up with people they don’t always socialize with.
We had a Cheerio stacking competition, which was pretty fun, and allowed for everyone to do some work.

Here’s the document if you want to run the task. I’ve tried it with grade 9 and 10 (both academic and applied)
Everyone needed to be timed for a minute of cheerio stacking. Then they predicted how many Cheerios they’d stack for 2 minutes and 3 minutes. Next they graphed the slowest and fastest stackers data.

Finally we looked at how to make a photo finish with a full skewer. We looked at how many Cheerios of a head start would be needed to balance the competition, and then we tried to see the photo finish occur.

We had a few epic photo finishes!

Later we spoke to our work to create brave spaces in our classrooms. We gave examples of what we do to create a comfortable space for students to try new things. We showed an example of a dot talk, and had lots of great interaction and participation from our staff.

we talked about our first week in grade 9, and how we introduce thinking routines, and communication structures, and explicit discussion of mindset which will continue through the year.
Here’s the slide deck if you are interested.
How Many High Fives?
Today in grade 10 we explored how many unique high fives there were in the room. We defined a high five as unique when person A high fives with person B. If Person B then high fives person A it doesn’t count.
Some groups got right to making tables. We had 15 people in the room today.

Once the situation was explored and understood, we clarified thar one could not high five themself…that’s called clapping… we kept working on the problem.
some groups drew it in pictures. Each line represents a high five.

Other groups wrote out all the high fives that would happen in a list, then totalled them up.

They noticed some patterns, and were able to make an equation for the pattern.

Another group modelled what would happen with a small group. We know that with 1 person there are no high fives, and with 2 people there is 1, and with 3 people there are 3, and with 4 there are 6. We kept adding more people to the group and they did the high fives and counted. Eventually a pattern was noticed, and identified as quadratic since the 2nd differences are all 1.
Some new learning today is that the “a” value is going to be half of the common 2nd difference.
The table could be extended backward to find the constant, c, 0 persons have 0 high fives, so the constant is 0. Next a point was subbed in for x and y and b was calculated.
There were some neat graphs that were made. This group showed the number of high fives per person, and total.
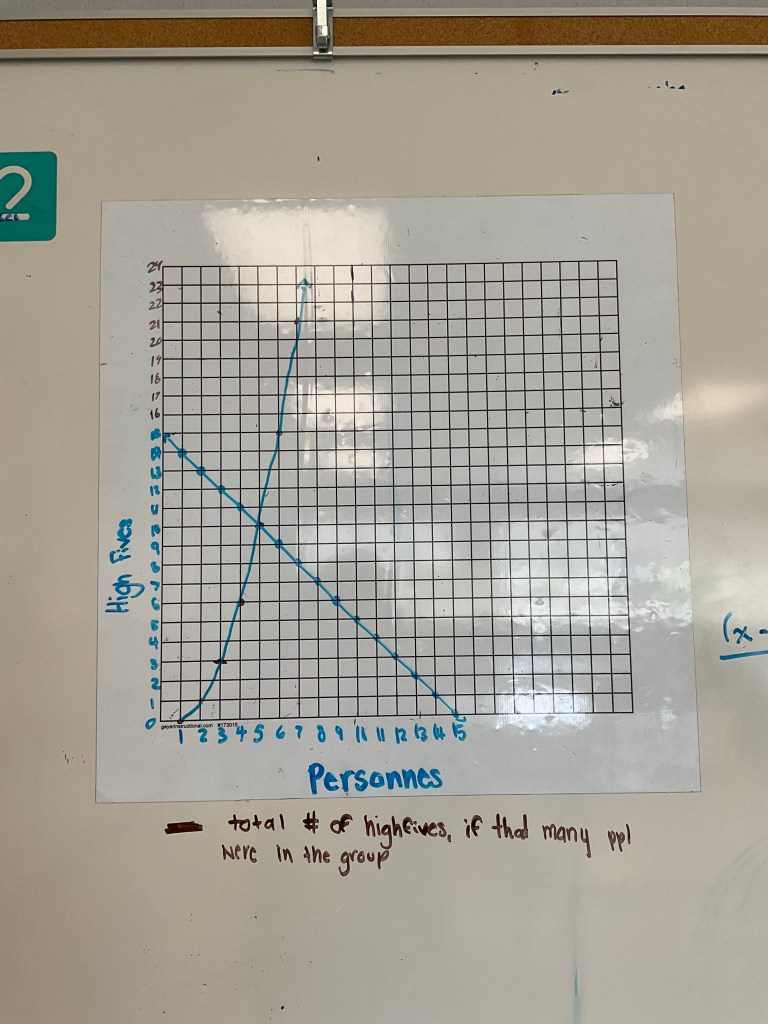
Others were looking for different patterns relating the high fives to the square of x.

It’s fun to look for and explore patterns, and practice expressing them in multiple ways.
Following this task we practiced a bit of modelling of visual patterns, and a few tables. Here’s one where you can model it in standard form, and again in vertex form, depending on how you view it.

We’re getting ready for our culminating task which uses tables to analyse the trajectory of a catapulted pompom. We’re going to be ready!
Test Talk
Today we tried something new. I’ve been torn for a while about how our learning model values collaboration and verbal communication, but that we are not valuing that on assessments. I was inspired by Howie Hua, a math influencer to try his Test Talk strategy.
We had pencils on the floor, and for 5 minutes students could look at the test, and talk with their peers about the test, and math, and strategies.
It was interesting to feel the tension in the room dissipate when they learned that we were going to try this strategy.
I think with time, students would adapt to reading the test over first, and checking in with themself to see if they know how to do the question, and then communicating with others around them to talk strategy, or ask questions.
It might give students an idea of where to begin, and what questions to leave to the end. It will encourage them to forge bonds with all of their peers so they can ask anyone anything.
It will also encourage students to be present on test day, because it’s hard to replicate this when writing the test alone at a later date.
The tests then happened as normal. Some students needed more time, but many were able to get it all done within a period.

Review
Grade 10s have a test tomorrow. We spent the first half of the period reviewing some trigonometry problems at the walls. It’s so great to see their interaction and helpfulness. We’ve made big growth in our team work since the start of term

I keep mentioning that my goal for the end of the term is for them to not need me, because they can do it themselves, or they have developed connections in the classroom and can work as a team to figure things out.
Some students are going above and beyond and when asked questions, will not give direct answers, but will ask good prompting questions, to encourage their peers to keep thinking.
It’s lovely for them to recognize the importance of arriving at the answer on one’s own, and not stealing moments of discovery away from their peers.
I’m witnessing students checking their work for reasonableness, inspecting their work for their common mistakes, and reaching out to others to confirm what they are doing.
The second half of the class students were working on their package of review problems. Doing work that is a bit more independent, because tomorrow’s test will be their big independent moment.
I’m very proud of this group! Looking forward to a good test day tomorrow.