Fraction Decimal Percent Clothesline
This morning we worked on understanding the connection between fractions and decimals and percents.
I prepared some cards (I cut index cards in half) and put decimals on some, fractions on others and percents on others. The values ranged from 0 to 2.5, and I tried to include equivalent representations, and also some interesting things like repeating decimals.
I split each pile of cards up so each table group had a different mix of cards and I instructed each group to sort the small pile on their table and to be sure that they have them in order from smallest to biggest.
Next I asked for a volunteer from each group to bring their biggest value up to the board and decide what was the biggest of the big values, and we established one end of our continuum. We did the same with another volunteer from each group comparing the smallest values to determine the other end of the continuum.
Next we had the entire class up organizing all of the cards into the right order on the whiteboards across the room. Students placed things that they thought were equal in a vertical list. We needed to do some discussing about whether 0.5% and 0.05 were the same thing.
Finally we worked on spacing out our values well, so we set some benchmark values of 0.5 and 1 and 1.5 and 2 and 2.5 equally spaced on the board, and tried to assemble a scaled version of our list.
I was impressed that there were some great conversations happening as students were comparing values. Many converted things to decimals to compare, but some were using their knowledge of percents and looking at fractions with the same numerator and different denominators, or same denominators and different numerators to compare.
It took about half a period including a lot of discussion. This type of activity could work well for doing place value, or scientific notation too. I have done something similar looking at radians in a 4U advanced functions class, where we made the clothesline on an actual string which we took down off the board then assembled into a circle, and we could see how good our spacing was since 2π radians should be a full circle.
Beading Progress
We have been working with our school board Indigenous Program team to work on a math project. We have been doing loom beading based on designs that students made. They need to be able to talk about the math that they use in their designs once they are finished.
Some of the math that we can see and talk about are:
- number of beads used (area model)
- fraction (ratio, decimal, percent) of beads of a certain colour
- symmetry
- reflections or rotations
- angles
- slopes
- proportional reasoning (e.g. for every pattern repeat of 4 rows we need to add 5 red beads)
- shapes
One student gave each digit from 0-9 a different colour, and then used their beading to express the value of pi. There are so many possibilities with this task!
While working, students are also reminded of teachings shared with us by an Indigenous beader, who spoke about how we need to put good thoughts and intentions into our work, and if we are feeling frustration we need to take a step back and take a break. This skill and self awareness is important for math too, as sometimes we will need to take a break if feeling frustrated.
We also appreciate the teachings about including a spirit bead in our work, either by chance or on purpose. Having a bead out of place is not a disaster, but rather celebrated as a feature to be sought out and discovered, as a way to encourage people to look closely and appreciate the details in the work. In math too we are working to not view mistakes as a disaster, but rather a moment for learning, and something that can be looked at more deeply.
We will need to return to this task in a while to remove our beading from the loom and glue hide to our finished products.
Concept Circles for Exploring Exponents
We’re working on understanding what exponents mean, and how to represent them. To explore this topic today we used a concept circle framework at mild, medium and spicy levels of challenge.
Inside each concept circle, a manipulative is given, which will be used to create the models. We used toothpicks for x, skewers for y, and plasticine to connect them all together
Here are some photos of what students showed. The ideas to tackle with this circle is the idea of brackets, and how 2x2 and (2x)2 are different. What is in the brackets becomes the side length of the object. We also explore the difference between having an exponent of 2 and 3. We can explore visually how (2x)2 = 4x2, and how (2x)3=8x3.
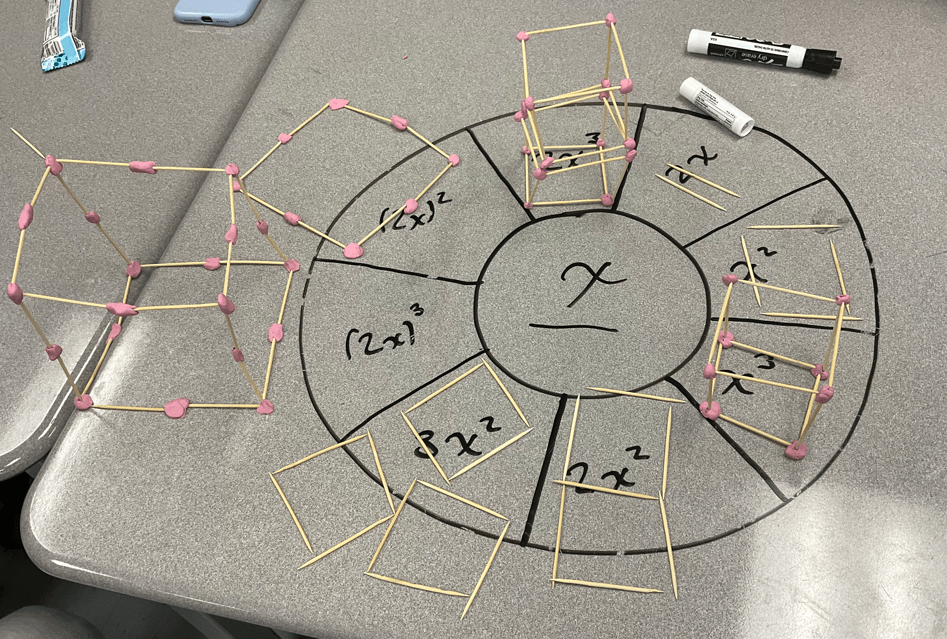
For the medium level, we introduce “half”, we talk about half an x, and half an x2 and half an x3. We can talk about how the hypotenuse of the (1/2) x2 needs to be longer than 1 toothpick. We reinforce the idea of what is in the brackets is the dimension of the object. We can explore visually how (1/2x)2=1/4x2, and how (1/2x)3=1/8x3. We also review distributive property, and show how x(x2+x) can be represented as x3+x2.
For the spicy level, students explored how to represent an x2y and an xy2 as rectangular prisms, and also looked at (x+y)2 and how it is not equal to x2+y2.
At the end of the class, some students used their creativity to build a super mega cube, a (2y)3.
It has been pretty powerful for students to understand the difference between algebraic expressions using algebra tiles and now these toothpick figures. Students have a very solid idea about what like terms are, which will come in handy in future equation solving problems, as we move to more symbolic representations.
We’re back!
School’s back on, and we’re working hard.
We’ve got our adolescent care workers in talking to us about the supports that are available for everyone this term.
Getting back in the building
We’re in teacher training for the 2020/2021 school year, and all the challenges that it brings.
Looking Forward
Hello everyone, happy summer! Congratulations on finishing up a very unusual term.
We are not sure yet what we will be doing in the fall, but I’m sure it will be different from what we’ve done before. In the mean time, be safe, wear a mask, stay away from people.
For those of you who would like to do some extra practice/review I suggest knowledgehook (grade 9s you can use class code gum4578 and have access to lots of missions and review questions)
khanacademy has lots of videos and questions and can help you fill some gaps in your understanding.
For those of you wanting to work on your multiplication skills. Here are the Five Minute Frenzy sheets that we got pretty good at last year.
You could also play around with desmos and see if you can create some amazing art!
Have a good summer and keep in touch.
Mme Bearse
Gathering Information
Angles
It seems like ages ago, but we worked with blocks to show lots of things about angles before schools were closed. Here are my pictures, for use in our learning portfolios.
We also learned that the interior angles of a triangle add up to 180 degrees, and the interior angles of a quadrilateral add up to 360 degrees. Both of these can be proven by creating a triangle (or quadrilateral, as shown), labelling and identifying the angles, and the ripping the shapes up to separate the angles.
The angles then ca be reassembled together, and in this case we see that they go all the way around a circle or 360 degrees. In the case of a triangle, they all come together to make a straight line, or 180 degrees.
We next had a look at desmos geometry, and we investigated how joining the midpoints of any quadrilateral will create a parallelogram in the middle.
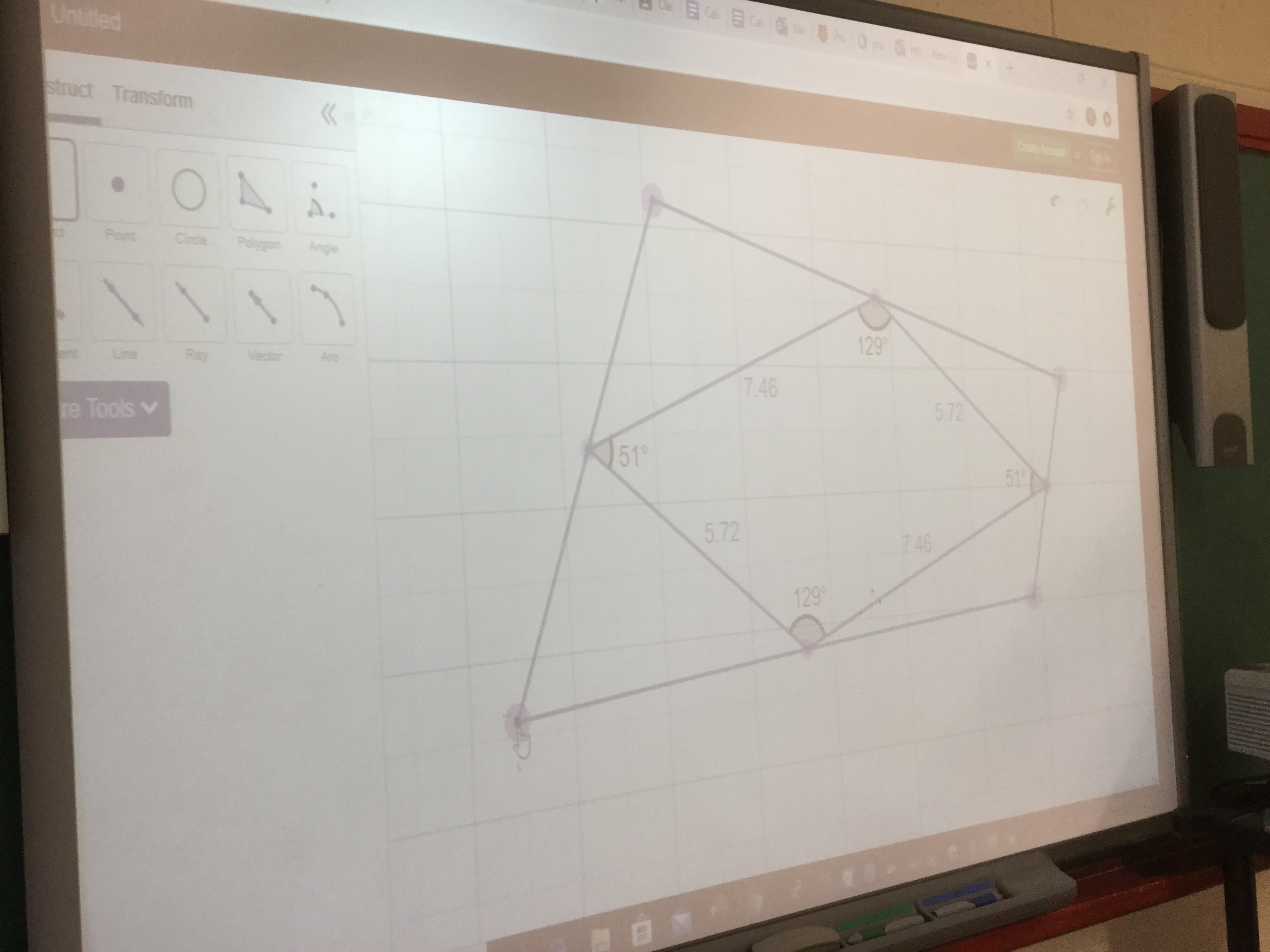
We can prove it’s a parallelogram by measuring angles. Opposite angles are congruent. Also parallel sides will be the same length. With desmos geometry we can drag and drop any of the corners to shift the shape, and see that the resulting interior quadrilateral is always a parallelogram!
Which one is bigger?
In 1L we are now looking at triangles, and other shapes. We wondered which was bigger, the rectangle or the triangle….
or which was bigger, the rectangle or the parallelogram….
We had a good discussion, and compared the two. Each of the shapes has the same area, as they were made by cutting the rectangle along the diagonal, and then rearranging the pieces. The perimeter is not the same for the shapes though!
We determined that the area of a triangle is half of the area of the rectangle that it came from.
First math test
First grade 9 math test today! We prepared well, and are ready to show what we can do. We know that the first test is often a learning experience!
Ms. Bearse's Site 