Painted Cube
Today I was invited to lead the painted cube problem in a colleague’s grade 10 math class. We are working on modelling and representing, creating equations, tables and graphs.
The problem: imagine a 3x3x3 cube that is dipped in paint, then dried. The cube is then disassembled, and we need to determine how many little cubes had 3 sides painted, 2 sides painted, 1 side painted or no paint at all.
As we worked through the task groups were prompted to try a 4x4x4 or 5x5x5 or nxnxn cube.

Groups had different ways to represent the number of painted sides. Many did drawings, and made tables.

Groups realized quickly that using a 3D model was really helpful. We used linking cubes to build different sized cubes. Some used colours as a legend for the number of sides painted, which was a neat idea.

It was excellent to see groups connecting the physical representation of the cube, and the algebraic representation. We saw that there was a quadratic equation which was connected to squares on the face of the cube, and a cubic equation that was connected to the interior cube.
Students made tables of values and saw that one relation had first differences that were the same, one had second differences that were the same, and one had third differences that were the same.

Students made graphs and saw trends. They explored all kinds of relationships, finding some patterns that have piqued my interest.
It was a lovely way to end our week. Good job grade 10s.
Introduction to Pseudocode
Today we had a busy day. We worked on multiplication skills, and had our first quiz, and then we started to learn about pseudocode.
We watched this video and debriefed about how it shows specific instructions and how important it is to be clear with our communication. We also talked about feeling the emotions and frustration sometimes in math, and how we can manage those feelings.
We then had a challenge! Groups had 2 puzzles to put together.

Each puzzle was made of lines of code that we had to out in the right order. The students told me that they had learned some Python last year, so this was an easy task for most. We saw that we need to initialize variables first, then input values, then do calculations. We saw that there is special syntax, * is multiply / is divide and ^ is exponent. We will build on our skills bit by bit over the term. We are not learning a coding language but we are working on the logic and writing it in pseudocode.
Word Problems
In Grade 11 we’ve been working on word problems and applying our skills with quadratics.

We work in random groupings each day, so we are getting to know each other and to work well with each other. It’s not always easy to know how to solve problems. We are building our confidence in starting problems, and making a plan to get to the answer.

It was interesting to see how various groups decided to place the bridge on the graph. Some placed the y axis at one of the foundations, others placed the y axis as the axis of symmetry of the parabola. Some decided to use vertex form, and some decided to use factored form. No matter what, we all got to the same “a” value which was a neat observation to bring forward in consolidation. There can be many correct models, and many paths to get to them.
This problem was fun. We worked on this one until the end of class, and left it as a cliff hanger, and started it again the next day.
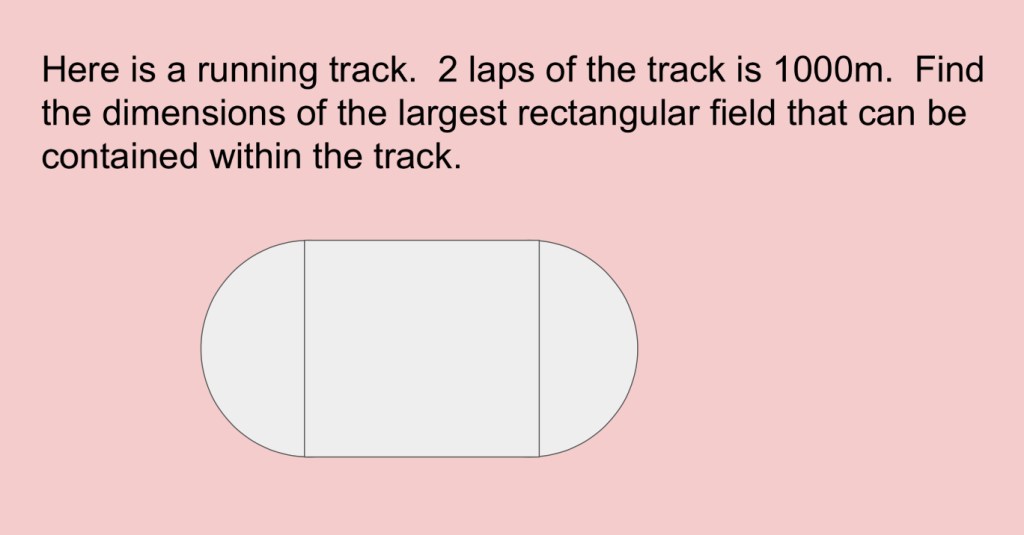

There was a lot of perseverance while working on this one. Reading and re-reading and making sense of how to use all the words was an interesting challenge. We wanted to maximize the area of the rectangle, so we need an equation for the area of the rectangle, and then we need to make sure that it is in terms of one variable, and THEN we need to find the vertex (maximum). Some groups missed that we are maximizing the rectangle. Some groups needed prompting about substitution, some needed help visualizing where the parabola is, because it’s not evident in the drawing that there is a parabola.
Today we started the class by finishing the problem. Some students had come in at lunch to try it again. We are developing more than just skills with finding the vertex, we are getting better at modelling a situation, creating equations, substituting when needed, and then finding the vertex.
It’s an impressive sight to see all 34 students engaged and working hard. It’s been a fun 2 weeks so far!
Plotting Points
Grade 9s have been working on introductory skills, and today we looked at plotting points and determining composite perimeter and area.
Groups were given a list of points to plot. Each set made a composite shape made up of rectangles.

They worked well together and remembered how to plot positive and negative values, and then cut up the region to calculate the area. They know the perimeter is the outside edges.
Our next task was to plot points from a table of values

We each chose different side lengths for squares and calculated the perimeter and area and kept the values in the table. We made graphs of the tables and saw that the perimeter data is linear and the area data is non linear.
Beans Update
I’m working with a grade 10 applied math class this semester introducing data collection and modelling tasks. Today we looked at the beans that we attempted to germinate over the past week. We opened up the sandwich baggies and unwrapped the paper towel and noticed thar some beans sprouted, and some rotted, becoming slimy and moldy. There were some different fungus too!

We noted the fraction of the beans that germinated and we will compare that to our predictions we made before planting.
We put the beans in little pots of soil and labelled each one with a popsicle stick. Each bean has a name so we can track the growth of each bean over time. We watered the little pots and have them in a clear bin by the window.
Our data tables are ready for when the beans start to grow. We will be watching every day for signs of sprouts, and adding water as needed.
Completing the Square
Locker Task
I was working with 2 different MTH1W classes today, introducing the locker problem. It always impresses me the creativity that the students show as they approach the open questions.
Here is the question: There are 100 lockers and 100 people. The first person opens all the lockers. The 2nd person closes every second locker, the 3rd person changes (open/closed) every third locker, the 4th person changes every 4th locker (and so on). After 100 people have gone past, which lockers are open.

We had groups who drew the 100 lockers and went through each opening and closing them with various symbols ans colours. Some groups modelled the first 10 or 20 lockers and wrote the status of each locker after each person passed by the lockers. This method was easier to troubleshoot. One group used a different colour for each person, and then noticed that if there’s an even number of dots then the locker is closed, and if there’s an odd number the locker is open.
one group was very keen on proving that all prime number lockers were closed. Another group focused on the lockers, and which people touched them, and if it’s an odd number of people then the locker is open.
Others saw the pattern of 1,4,9,16 and could see that it’s perfect squares, and some people saw that in the end that we skipped over 2, skipped over 4, skipped over 6, skipped over 8, and they worked out the pattern from there.

We consolidated the ideas of square numbers, and how they have an odd number of factors since there is a number that is multiplied by itself.
It’s fun to watch students get better at persevering through a challenging problem. We’re off to a good start already!
Locker Problem
There are 100 lockers, and 100 people. Person 1 walks past and opens all the lockers. Person 2 walks past the lockers and closes every 2nd locker. Person 3 walks by and changes the stare (open/closed) of each 3rd locker. This continues and each person walks past changing lockers depending on their position, the 5th changes every 5th locker and the 10th changes every 10th locker etc.
At the end, we want to know which lockers are open.
Students worked so hard in groups to solve the problem. Representing the information was a challenge!

Many groups started to notice some patterns, and then they extended patterns to cover the 100 lockers.

People caught on to the fact that the open lockers will be the ones that are square numbers. This is because they have an odd number of factors. We also noticed that the numbers go up by 3,5,7,9,… and that the 2nd differences (the change in the differences) is 2 each time.
After our debrief and consolidation we took a minute to email families. Students filled in some blanks in an email template, and sent it to me as well as their family. We keep emailing over the course of the term to keep communication going, and to provide moments for reflection.
Parabola Day!
We started our review of quadratics today and also introduced the concept and notation for domain and range.

We looked at the visual pattern, modelled it with a function, made a table of values and a graph. We used our prior knowledge to determine the vertex (by factoring, quadratic formula, or knowing that the axis of symmetry is x=(-b)/(2a)). Once the axis of symmetry is found we sub that in as f and calculate the y value of the vertex. The range is going to be based on this value.
I was really proud of how students are helping others, and how many different strategies they are using.

