Ms. Bearse's Site

Période B: Mardi

Bonjour les 9e: Dans vos groupes, notez les choses que vous REMARQUEZ et les QUESTIONS que vous avez/que vous voulez répondre.

ACT 2: Vous allez faire le travail!

Quelle information voulez-vous savoir?

ACT 3:

Les questions supplémentaires:

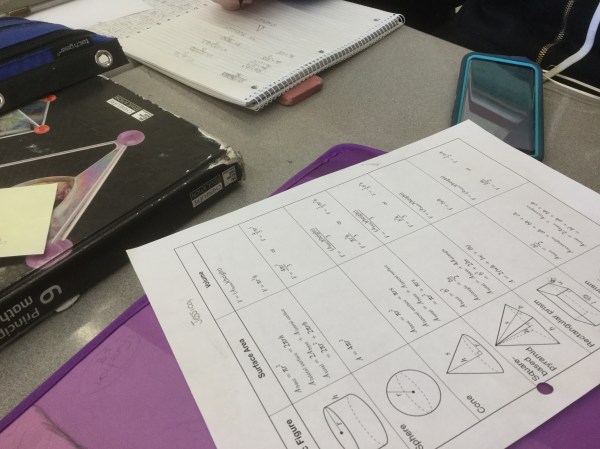
1.  Combien de façons pouvons nous trouver pour modifier le cylindre pour DOUBLER le montant de maïs soufflé.  Lequel prend le MOINS de papier de surplus?
2. Pouvons nous utiliser le même montant de papier, et créer un contenant qui contient PLUS de maïs soufflé?
3. Si un théâtre demande 5$ pour le cylindre plus court, combien est-ce qu’ils devraient demander pour l’un qui est plus mince?

Desmos geometry  helps us to visualize and manipulate some interesting geometric properties.  We can create medians (les médianes) and perpendicular bisectors (les médiatrices).  We can also adjust drawings and see if relationships among points and lines change.

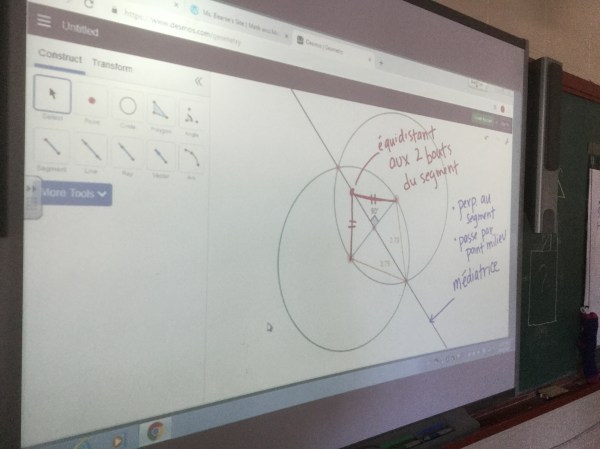
From a simple construction, we were able to create a perpendicular bisector (médiatrice)

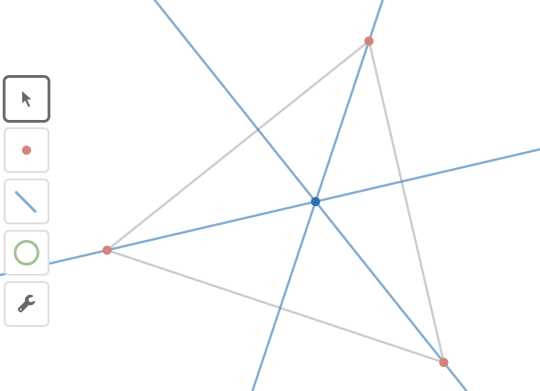
We also looked at a median for a triangle, and how medians always intersect at the centre of gravity.

In grade 9 we looked at a variety of pyramids and their related prisms (same base and height).  We estimated the number of times the pyramid could be filled with water and emptied into the prism to fill it up.  Guesses ranged from 1.75 times to 3.5 times, with most of the class finally settling around the guess of 2 times.

However minds changed quickly when the pyramid was poured once into the prism.  After that we all agreed that it’d take 3 pyramids to equal the prism volume, or that the pyramid was 1/3 the volume of the prism.

 We set about to build a pyramid with the volume of 300cubic centimeters. We needed to do some calculations, and figure out what dimensions would work.  Many groups figured out dimensions of a prism that has a volume of 900 cubic centimetres to start with.

We then figured out what to cut out of the paper.

Some pyramids were short

Some were tall
And some started to look more like a prism than a pyramid, but the good things about building with old file folders is that you can always start over!

Many groups had to start over, because for many their pyramids were too short.  Many built pyramids hoping for the height to be 9, but instead they measured the height of the sloped triangle sides to be 9, so the entire pyramid height would be smaller than that.

The pythagorean theorem is there, right inside the pyramid.  The height (black) and half of the base (pink) form the legs of the triangle, and the slant height (pink) is the hypotenuse.

h^2+(0.5b)^2=s^2

We had a few good pyramids by the end of class, and we also had a much better understanding of area and volume.

We experimented with squares, plotting area and perimeter against side length

We are making tables of values, visual models, graphs, and looking at the trends we see.

With the squares we noticed that perimeters increase steadily as the side length increases, and so we have a linear relation.  We also made a formula for calculating perimeter and noticed there is no exponent.  We compared the area graph, which is an increasing curve.  We noticed there is an exponent when we calculate area.  We also saw that the perimeter and area are the same if the side length is 4, because there is an intersection on the graph.

Our next experiment was all about hot water.  We boiled a kettle and then poured the hot water into a mug.  We took temperature measurements each minute and put them into a graph.

We made some predictions after the first few minutes…

Some of us drew lines that continued downward all the way to the bottom of the graph (the x axis) which would represent the temperature becoming zero.  Our classroom is ridiculously hot so we know the water can never get to zero!We need to be careful when extrapolating; we should think about what is happening, and what the limitations might be, or what the future values could be.  Each situation is different so we need to consider the details and constraints very carefully.

Great work grade 9s!

We are working hard to master our chapter 1 problem solving techniques.  We are writing out full solutions…

We are working together and making sure our solutions make sense

We’re also working on completing our study notes assignment that is due tomorrow.

Keep up the great work grade 10s!

Today in grade 9 we experimented with the sound produced when blowing over the neck of a bottle with more or less water in it.

We used the app “sonic tools” to determine the frequency, and we started out with a lot of water in our bottles (which creates a small air column), and we decreased the level of water between trials, which increases the column of air in the bottle.
Once we got going, we collected a lot of data in a relatively short time.

We learned how to use google sheets to make a graph from a spreadsheet.  Although it’s not ideal to use an ipad (graphs don’t format well) the computer version can make some great graphs.

This graph has the frequency on the vertical axis, it is what we measured, and it depends on the height of the air column.  The frequency is the dependent variable.  The height of the air column is on the horizontal axis, it is the independent variable, which we modified as part of our experiment.

We see that the graph is non linear, and fairly strong but not perfectly correlated, it is partial, and it is negative.

We worked on literacy test prep today

The focus was on text features, and how to approach multiple choice questions.

Grade 9s continued with their graphs from yesterday.

Some decided their graphs looked linear, and so they drew lines of best fit to model the trend.

Others weren’t exactly convinced the trend would be a straight line, so they added lines or a curve of best fit to model how the trend changed.

After everyone had their graphs, the goal was to predict how many cheerios would fit on two mystery circles.  One was a small circle, (that fell between data points on the graph), and another was really big, bigger than any other circle we had filled before. 

Estimates for the big circle ranged from 160-300 cheerios based on our various graphical models.

To see how close our estimations were, we filled the circle and counted.

Our total number of cheerios was 290

We learned a few things while working on this activity.  

1. Graphing by hand is tedious! 
2. When you need to use your graph to make a prediction of a larger value, you may need to make your graph bigger, and use a lot more paper.
3. Desmos scales the graph for you, and errors are fixed quickly.

We also learned that we can estimate within our data range with pretty good results.  This is called interpolation.  We had less success estimating outside our data range (extrapolation), which had to do with our choice of model and whether we used a line or curve of best fit.

We will continue to do experiments and graphs this week to get more comfortable with scatter plots.

Grade 9s worked hard to model the number of cheerios that could fit on a variety of circles.

The end goal is to be able to predict how many cheerios would fit on a different circle, like a cookie tin.

We measured dimensions, decided what variables to track, and then made data tables

We’re making graphs to see what the trend looks like.

We’ve had estimates that the trend is positive because the numbers are getting bigger in the columns, and that it will be weak because it’s hard to know exactly how many cheerios will fit on a circle, and because cheerios are of varying sizes.  We’ll see tomorrow how it turns out.

We have gone over many topics about functions and are heading toward calculation of average and instantaneous rate of change.

We looked at functions and determined with algebra if they are even or odd.

We also looked at inverses to be sure we understood how to calculate them and interpret our answers.

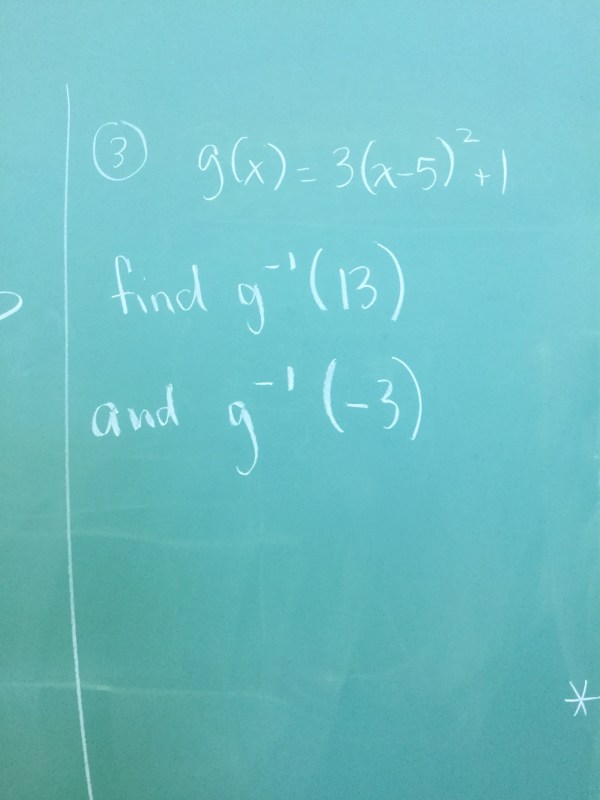
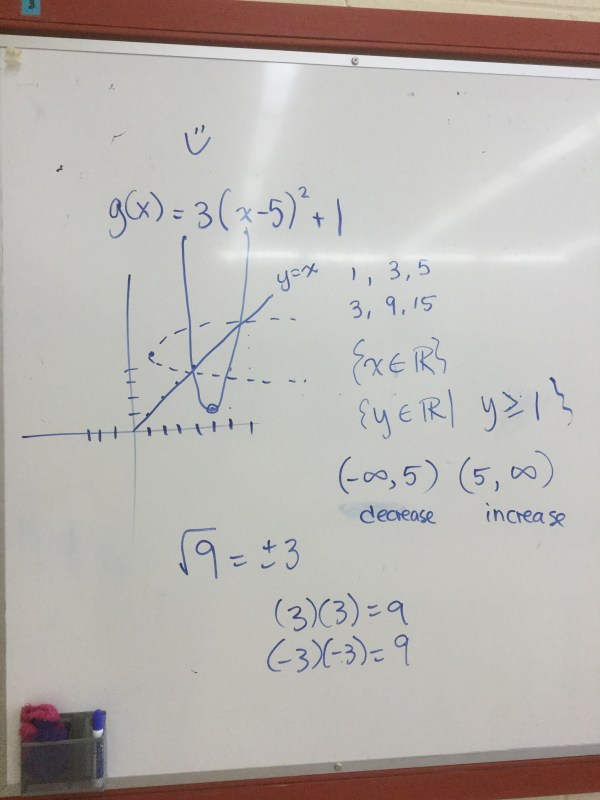
Here’s a sketch of the function and its inverse relation (which is not a function).

And here’s the algebra:swap x and y and isolate y.

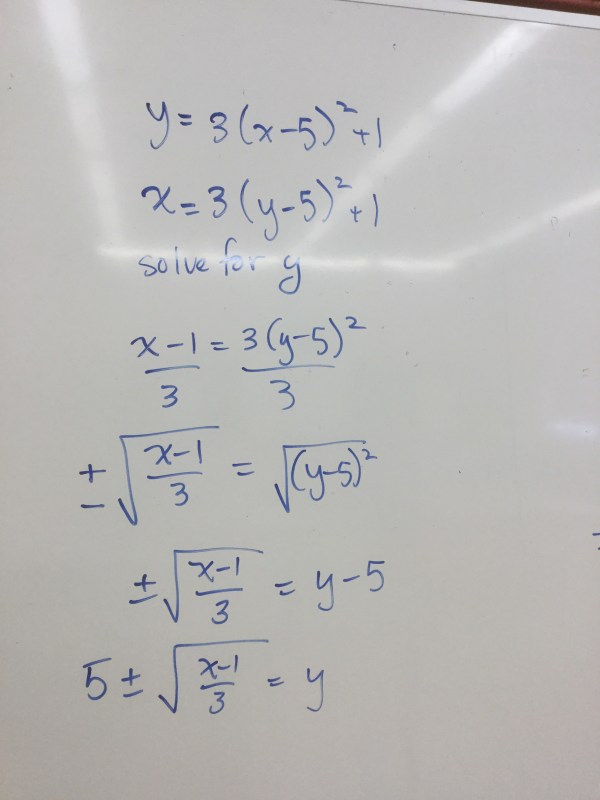
When looking for the inverse at 13 we get proof that it is not a function since we get two outputs.

And the inverse at -3 doesn’t exist (no real value), because we cant take square roots of negative numbers, which makes sense when you look at the graph, because there are no points on the graph of the inverse that correspond to x=-3.